Geometry Angle Relationships Worksheet Answer Key Revealed
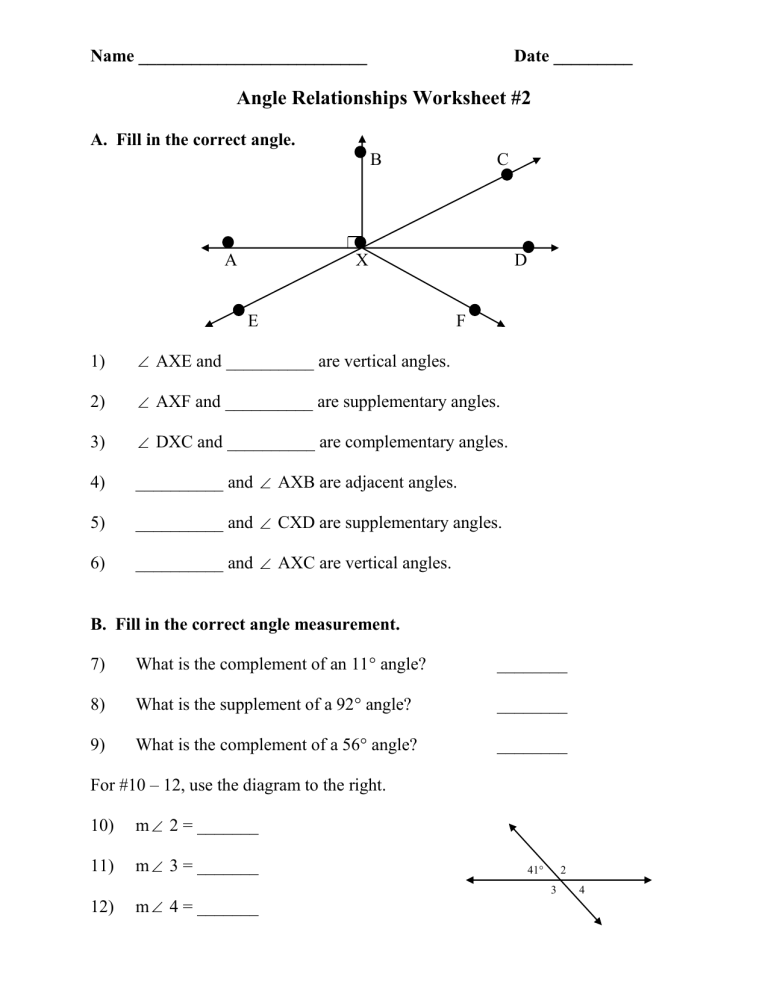
Understanding angle relationships in geometry is pivotal for students, as it forms the bedrock of more advanced mathematical concepts. Whether you're diving into trigonometry, learning about geometric proofs, or exploring the intricate world of spatial reasoning, knowing how angles interact and relate to one another is essential. This long-form blog post is designed to guide you through the key concepts related to angle relationships, offering you a detailed answer key to a typical worksheet on this topic, and providing insights to deepen your understanding.
Understanding Basic Angle Types
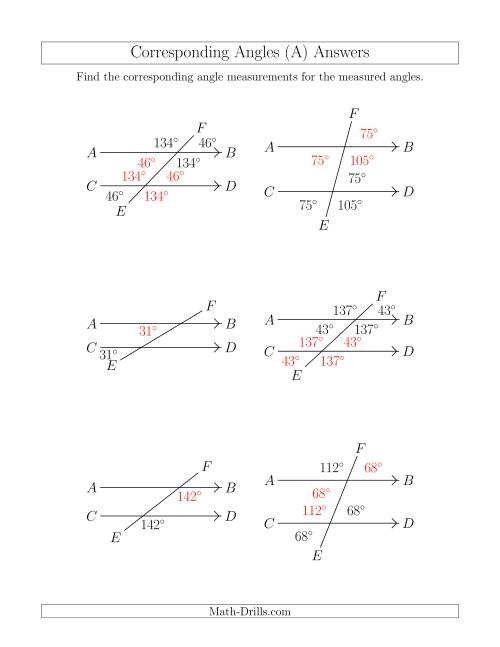
Before we delve into the complexities of angle relationships, let's refresh our knowledge on the basic types of angles:
- Acute Angle: Less than 90 degrees.
- Right Angle: Exactly 90 degrees.
- Obtuse Angle: Between 90 and 180 degrees.
- Straight Angle: Exactly 180 degrees.
- Reflex Angle: More than 180 degrees.
📐 Note: Angles can be further categorized by their position relative to a transversal and two or more lines they intersect, forming various angles types and relationships.
Key Angle Relationships

Now, let's explore the fundamental relationships between angles:
Complementary Angles

Two angles are complementary if their measures add up to 90 degrees. For instance, if Angle A is 35 degrees, then:
- Angle B would be 55 degrees (90 - 35 = 55).
Supplementary Angles

Two angles are supplementary if their measures sum to 180 degrees. If Angle C is 130 degrees:
- Angle D would be 50 degrees (180 - 130 = 50).
Vertical Angles

Vertical angles are formed when two lines intersect. They are opposite each other and are equal in measure:
- If Angle E = 70 degrees, then Angle F (its vertical angle) would also be 70 degrees.
Linear Pairs

When two angles share a common side and a common vertex, forming a straight line, they create a linear pair, summing to 180 degrees:
- If Angle G is 110 degrees, Angle H would be 70 degrees.
Adjacent Angles

Adjacent angles are angles that share a common vertex and a common side but do not overlap:
- If Angle I is 45 degrees and Angle J is adjacent, the measure of Angle J could vary as long as they don’t overlap.
🔄 Note: Adjacent angles are not the same as supplementary angles unless they form a linear pair.
Exploring Angle Relationships in a Geometry Worksheet

Let's look at a sample geometry worksheet and its answer key to understand how these concepts are applied:
| Problem | Answer |
|---|---|
| Find the measure of Angle A if it is complementary to a 55-degree angle. | Angle A = 35 degrees |
| If Angle B is supplementary to a 120-degree angle, what is the measure of Angle B? | Angle B = 60 degrees |
| Angle C and Angle D are vertical angles, and Angle C is 65 degrees. What is Angle D? | Angle D = 65 degrees |
| Angle E is part of a linear pair with an angle of 105 degrees. What is Angle E? | Angle E = 75 degrees |
| If Angle F is adjacent to a 30-degree angle and they form a right angle together, what is Angle F? | Angle F = 60 degrees |

Applying Angle Relationships

The understanding of angle relationships goes beyond mere worksheet answers. Here are some ways these concepts can be applied:
- Architectural Design: Architects rely on the principles of angle relationships to design structures, ensuring walls meet at right angles, or staircases align correctly.
- Navigation: Pilots and sailors use bearings, which are essentially angles, to navigate. Understanding how these angles relate helps in determining accurate routes.
- Engineering: Engineers utilize these concepts in structural analysis, where understanding stress distribution involves angles and their relationships.
In summary, a firm grasp of angle relationships enhances one's ability to solve various geometric problems and applies directly to real-world scenarios. It's not just about knowing the rules but also about how they interconnect within the broader tapestry of geometry. This foundational knowledge lays the groundwork for advanced topics, making it indispensable for students of mathematics.
What are the practical uses of understanding angle relationships?

+
Understanding angle relationships is essential for fields like architecture, engineering, navigation, and design. They allow professionals to ensure structural integrity, precise navigation, and aesthetic balance in their work.
How can I remember which angles are complementary and which are supplementary?
+
A handy mnemonic device is “C” for complementary (think of the “C” for “corner,” like the right angle of a corner) which adds up to 90 degrees, and “S” for supplementary (think of the “S” stretching into a straight line) which adds to 180 degrees.
Why do vertical angles have equal measures?
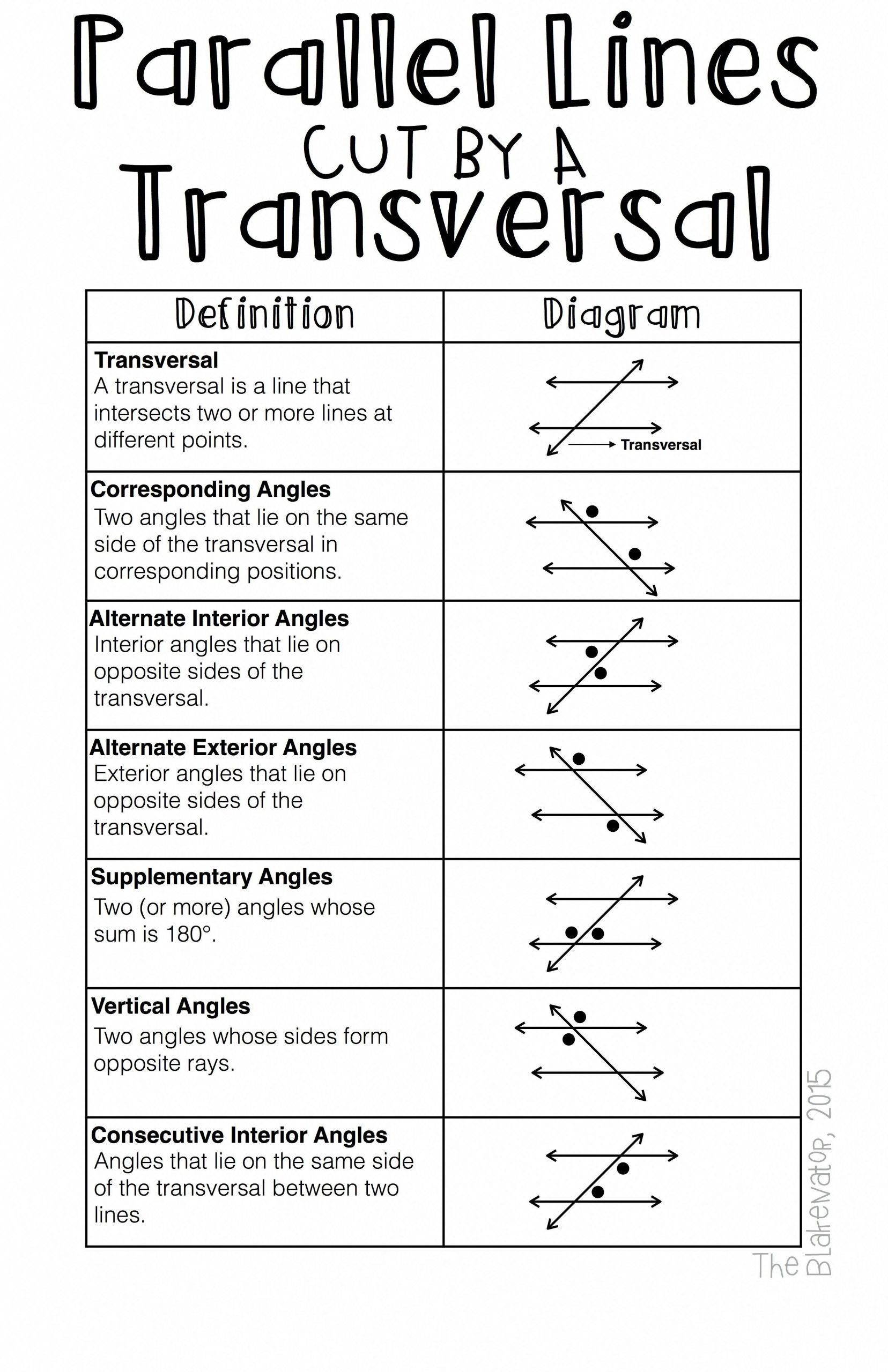
+
Vertical angles are opposite each other when two lines intersect, and by geometric proof, they share the same properties due to the intersecting nature of the lines. This symmetry ensures they are always equal in measure.