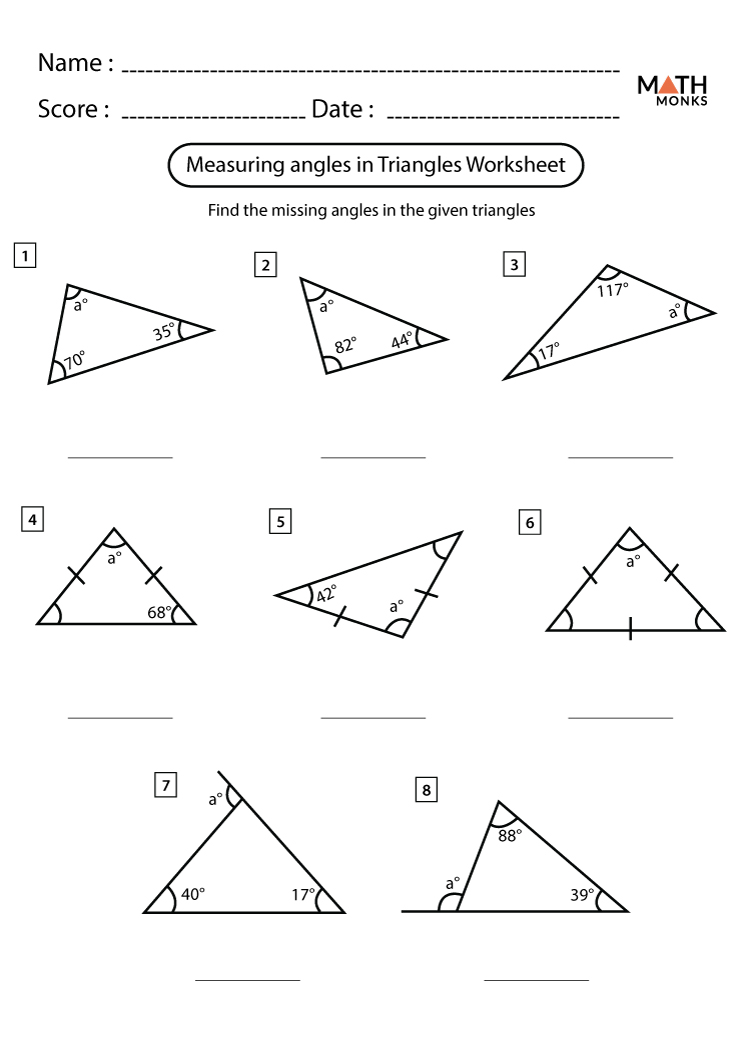
5 Tips for Mastering Geometry Angle Worksheets

Mastering Geometry: Angle Worksheets

Geometry, with its abstract concepts and intricate diagrams, often challenges students who struggle to grasp its fundamental principles. One of the foundational elements of geometry is the study of angles. Angle worksheets provide a structured way for students to practice and reinforce their understanding of angles. Here are five tips to help you master these worksheets:
Understand the Basics

Before delving into more complex angle problems, ensure you have a solid understanding of the basics. Key concepts include:
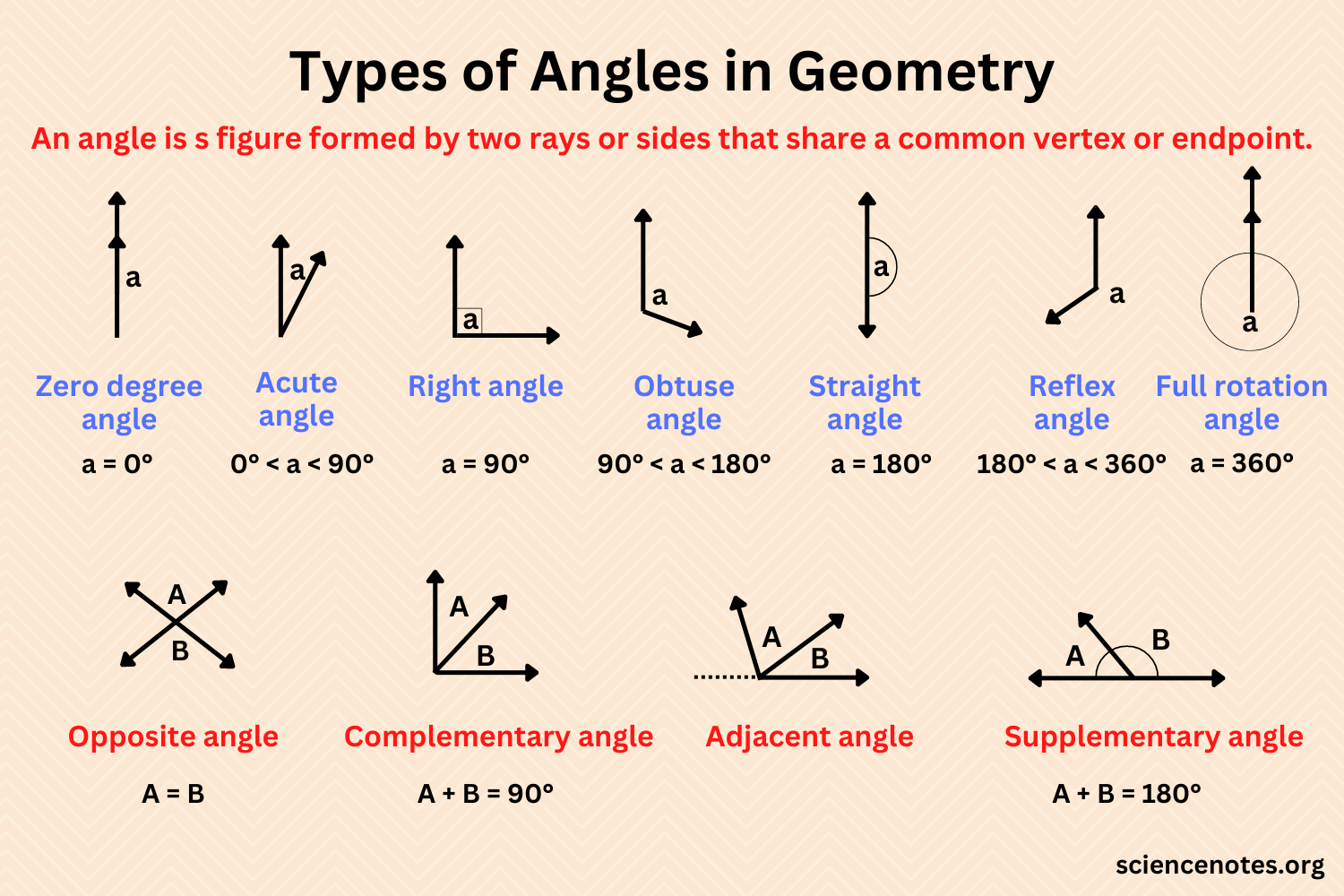
- Types of Angles: Recognize acute, right, obtuse, and straight angles.
- Angle Relationships: Learn about complementary, supplementary, adjacent, and vertical angles.
- Angle Measurement: Understand how to use a protractor correctly.
🔍 Note: A firm grasp of these fundamentals will make advanced problems more approachable.
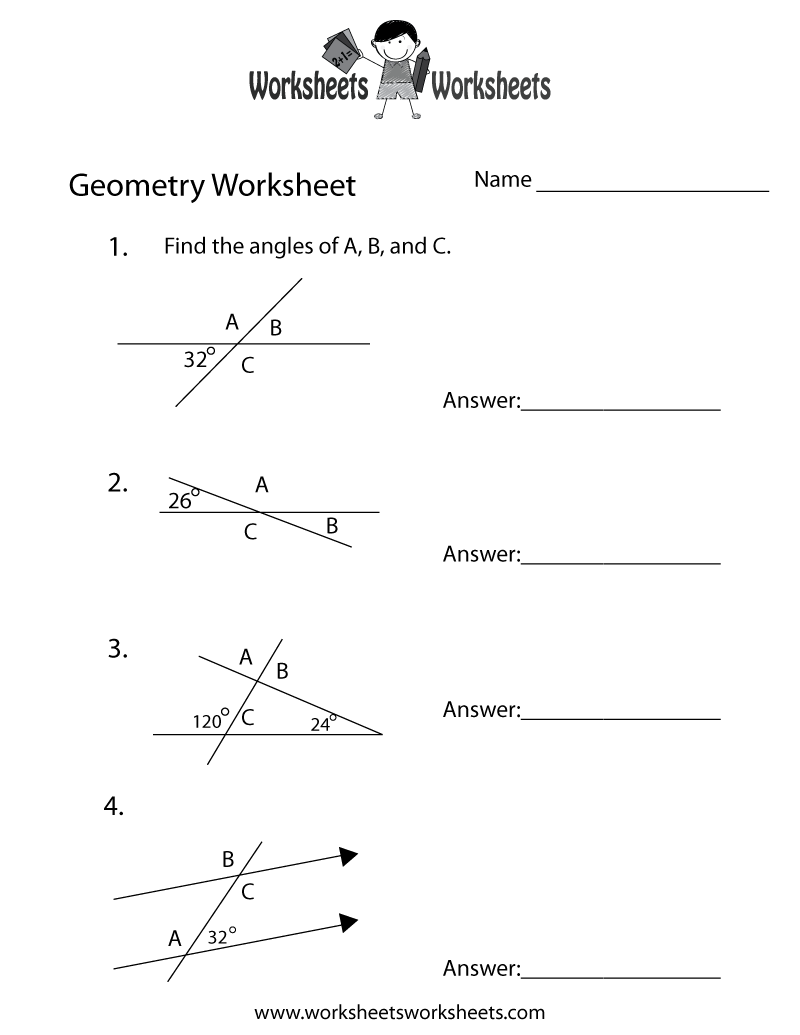
Practice Identifying Angles in Diagrams

Many geometry problems require you to identify and classify angles within complex diagrams. Here are some strategies:
- Label all angles clearly to avoid confusion.
- Look for recognizable shapes within the diagram that might help you deduce angle measurements.
- Use geometric properties like opposite angles of a quadrilateral sum to 360 degrees.
Utilize Visual Aids

Visual aids can be incredibly beneficial:
- Sketch your own diagrams if they aren’t provided.
- Use color-coding to distinguish between different types of angles or related properties.
- Physical manipulatives or digital tools like GeoGebra can enhance understanding.
Master Key Theorems and Postulates
| Theorem/Postulate | Description |
|---|---|
| Angle Addition Postulate | If a point lies on the interior of an angle, then the sum of the measures of the two smaller angles is equal to the measure of the original angle. |
| Vertical Angles Theorem | Vertical angles are congruent, meaning they have the same measure. |
| Linear Pair Postulate | If two angles form a linear pair, their measures sum to 180 degrees. |
| Parallel Lines Theorem | If a transversal intersects two parallel lines, then alternate interior angles, alternate exterior angles, and corresponding angles are congruent. |

Knowing these and applying them can significantly ease the process of solving angle problems.
Practice Consistently

Like any skill, mastering angles in geometry requires regular practice:
- Set aside time daily for angle worksheets.
- Try different types of problems to broaden your understanding.
- Review mistakes to learn from them.
By following these tips and consistently practicing with geometry angle worksheets, you'll find your ability to work with angles will improve dramatically. Remember, mastery in geometry, especially angles, comes not just from solving problems but from understanding the underlying principles and patterns that govern them.
Why are angles important in geometry?
+
Angles are crucial in geometry because they help define the relationships between lines, shapes, and their properties. They are fundamental to understanding geometric constructions, proofs, and real-world applications like architecture and engineering.
How can I make using a protractor easier?
+
To make using a protractor easier, ensure you align the base line of the protractor with one of the arms of the angle, read the measurement from the inner or outer scale depending on where the other arm falls, and double-check your reading with a straight edge to ensure accuracy.
What are some real-world applications of angle geometry?

+
Angle geometry is applied in various fields including:
- Architecture and construction to design accurate angles and slopes.
- Navigation, where angles are used to determine direction and path.
- Engineering, where angles are key in understanding forces and stresses.
- Art and design for perspective and composition.