7 Essential Tips for Geometry Angle Relationships

Angle relationships in geometry are fundamental to solving problems involving triangles, quadrilaterals, and other geometric figures. Understanding these relationships not only simplifies complex calculations but also enhances our visual spatial reasoning. Here are seven crucial tips for mastering angle relationships:
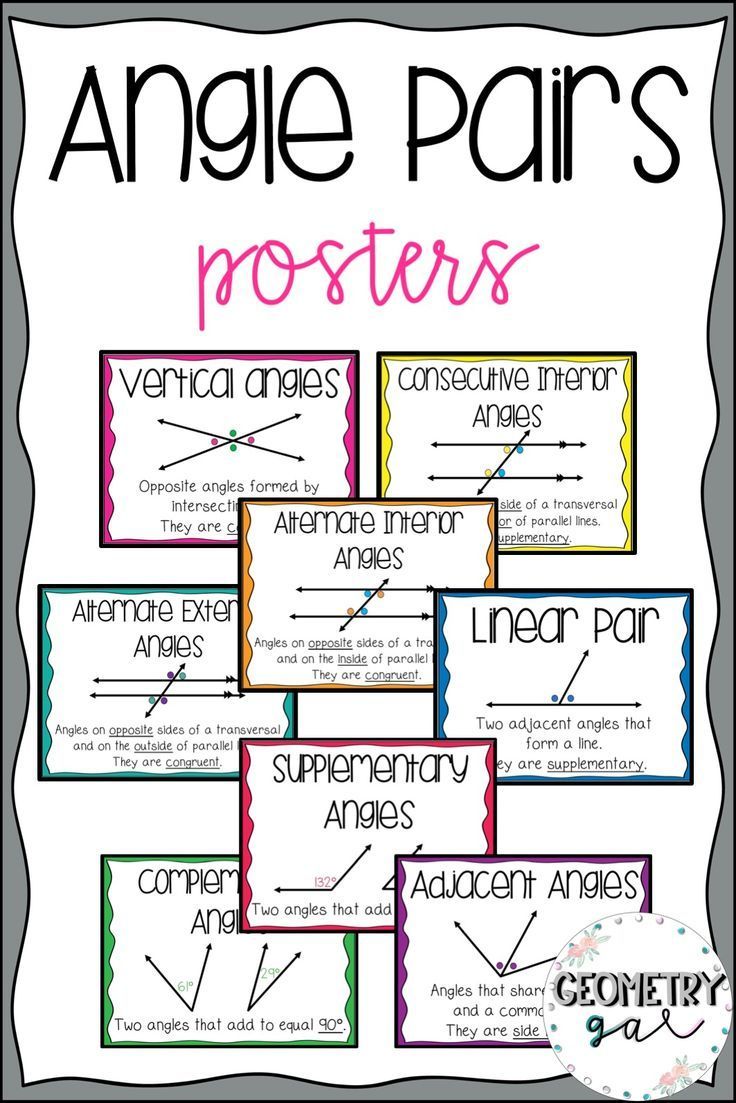
1. Recognize and Apply Types of Angles

Start with the basics:
- Acute Angles: Less than 90 degrees.
- Right Angles: Exactly 90 degrees.
- Obtuse Angles: More than 90 but less than 180 degrees.
- Straight Angles: Exactly 180 degrees.
- Reflex Angles: More than 180 degrees.
By identifying the type of angle, you can proceed with the appropriate geometric rule or theorem.
2. Complementary and Supplementary Angles

Learn about the sums:
- Complementary Angles: Two angles that sum to 90 degrees.
- Supplementary Angles: Two angles that sum to 180 degrees.
💡 Note: If two angles form a right angle, they are complementary. If they form a straight line, they are supplementary.
3. Understand Adjacent and Vertical Angles

Here are some key points:
- Adjacent Angles: Angles sharing a common vertex and side, but not overlapping.
- Vertical Angles: Opposite angles formed by the intersection of two lines. They are congruent.
Identifying these can often simplify problems involving intersecting lines.
4. Master Triangle Angle Relationships

In triangles:
- The sum of the interior angles is always 180 degrees.
- An exterior angle is equal to the sum of the two non-adjacent interior angles.
- If you know two angles, you can find the third using this sum.
5. Know the Angle Properties in Parallel Lines

When a transversal cuts through parallel lines, several angle relationships occur:
| Angle Pair | Relationship |
|---|---|
| Corresponding Angles | Congruent |
| Alternate Interior Angles | Congruent |
| Alternate Exterior Angles | Congruent |
| Consecutive Interior Angles | Supplementary |

These relationships make solving for unknown angles straightforward.
6. Utilize the Exterior Angle Theorem

This theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. This can be particularly useful when dealing with complex triangles or proving congruence.
7. Practice with Real-World Applications
To truly grasp angle relationships, apply them to real-life scenarios:
- Navigation: Use trigonometry to calculate angles of elevation or depression.
- Design: Understand how angles work in architectural design and art.
- Physics: Calculate trajectories, where angle relationships determine outcomes.
Understanding and applying angle relationships is key to mastering geometry. Whether you're solving for angles in a drawing, designing a structure, or working on real-world problems, these tips will enhance your ability to work with angles efficiently. Remember, geometry is not just about numbers and shapes but also about understanding how these elements interact in space, which is both practical and fascinating.
Why do angle relationships matter in geometry?

+
Angle relationships simplify complex geometric problems, making it easier to calculate unknown angles and understand spatial relationships in various shapes and scenarios.
Can you explain the concept of a “complementary” angle?

+
Complementary angles are two angles that add up to 90 degrees. They complement each other to form a right angle.
How do vertical angles relate in geometry?

+
Vertical angles are the opposite angles formed by two intersecting lines. They are always congruent, meaning they are equal in measure.