9 Essential Symmetry Tips for Geometry 9.5 Worksheet

Discovering the Beauty of Symmetry

Symmetry, a fundamental concept in geometry, plays a pivotal role in understanding the balance and regularity in shapes and patterns. Geometry, particularly at the 9.5 grade level, introduces students to various forms of symmetry which can often be overwhelming due to their complexity. This blog post aims to simplify these concepts by providing you with nine essential symmetry tips, tailored for the Geometry 9.5 worksheet, ensuring you can grasp, apply, and excel in this fascinating area of mathematics.
Understanding Line Symmetry

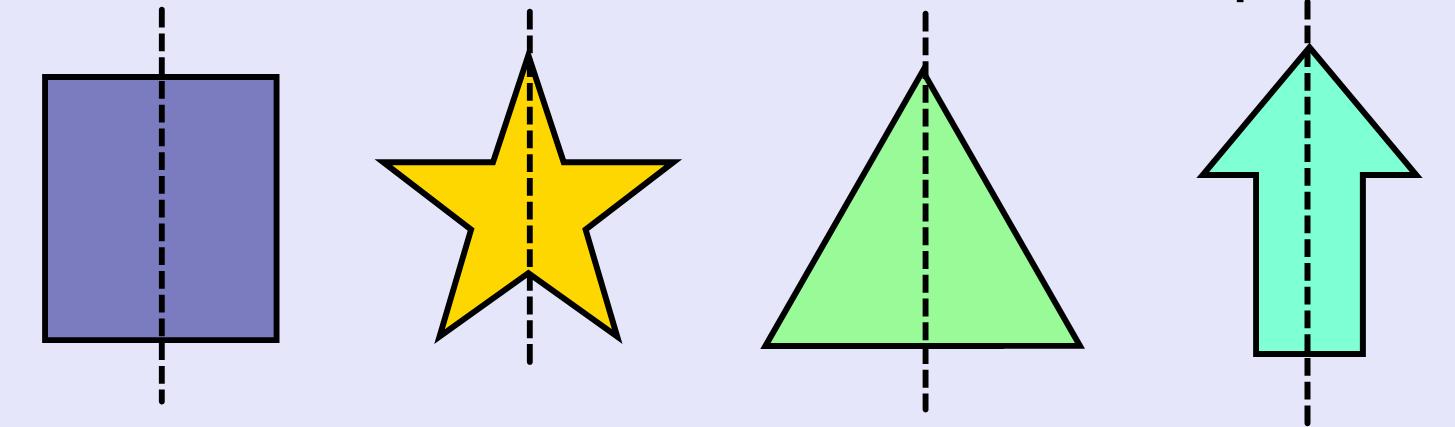
Line symmetry, also known as reflection symmetry, is where a figure can be divided by an imaginary line into two parts that are mirror images of each other. Here’s how to approach line symmetry:
- Identify Potential Lines: Look for imaginary lines that can split the shape into two symmetrical halves.
- Check for Reflection: Fold the paper along the identified line to check if both sides align perfectly.
- Practice Different Shapes: Use triangles, squares, circles, and even irregular shapes to understand how various forms exhibit line symmetry.
💡 Note: Remember, not all shapes are symmetrical. Some might have multiple lines of symmetry, while others might have none.
Exploring Rotational Symmetry

Rotational symmetry or order of rotation involves rotating a shape around its center, and at certain angles, the shape looks identical to its original form. Here are some tips for mastering rotational symmetry:
- Identify Rotational Center: Find the center around which the shape rotates.
- Count Rotational Order: Determine how many times the shape matches itself during a 360-degree rotation.
- Use Clock Analogy: Imagine the shape is on a clock face. How many times does it return to its original appearance?
Decoding Point Symmetry

With point symmetry or center symmetry, a figure remains unchanged when rotated 180 degrees about a point. Here’s how to tackle this:
- Find the Center of Symmetry: This is the midpoint of any line segment drawn between two corresponding points.
- Check for Correspondence: Each point should have a matching point on the other side of the center.
Translational Symmetry

Often seen in patterns, translational symmetry involves moving a figure along a line without rotating or flipping it. Here’s what you need to know:
- Identify the Pattern: Look for repeating patterns.
- Understand the Vector: Determine the vector along which the figure slides.
Practical Application of Symmetry

| Shape | Line Symmetry | Rotational Symmetry |
|---|---|---|
| Equilateral Triangle | 3 Lines | 3 Points |
| Square | 4 Lines | 4 Points |
| Circle | Infinite Lines | Infinite Points |

Applying Symmetry in Real Life
Understanding symmetry isn’t just about solving worksheets; it’s also about recognizing its applications in our world:
- Art and Design: Symmetry creates balance and harmony.
- Nature: Many plants, animals, and even crystals exhibit symmetrical patterns.
- Architecture: From ancient to modern, buildings use symmetry to create visually appealing structures.
Practicing Symmetry Exercises

Here’s how you can practice symmetry for your Geometry 9.5 worksheet:
- Draw and Identify: Draw shapes and identify their symmetries.
- Solve Symmetry Problems: Use existing symmetry exercises to solve for shapes’ symmetrical properties.
- Use Software: Utilize geometry software or apps for interactive learning.
Avoiding Common Mistakes

When dealing with symmetry, here are some common pitfalls to avoid:
- Confusing Symmetry Types: Line symmetry is different from rotational or point symmetry.
- Ignoring Asymmetry: Not all shapes are symmetrical, and it’s essential to recognize when they aren’t.
- Overlooking Minor Details: Even small discrepancies can break symmetry.
🌟 Note: Symmetry should be evident even when using symmetry tools like tracing or rotation software. If there’s doubt, double-check your work!
Exam Preparation Tips

To excel in your Geometry 9.5 worksheet:
- Regular Practice: Symmetry exercises should be part of your daily routine.
- Understand the Concepts: Don’t just memorize; understand why symmetry works.
- Ask for Help: Don’t hesitate to ask teachers or classmates for clarification on tricky concepts.
In this exploration of symmetry, we've covered a wide range of concepts from line symmetry to the more complex point symmetry. By grasping these core principles, you can not only answer questions correctly but also appreciate the beauty and order that symmetry brings to the world of geometry. The tips provided will help you navigate your Geometry 9.5 worksheet with confidence, turning what might seem like a daunting task into an engaging and rewarding journey.
What is the difference between line and rotational symmetry?

+
Line symmetry involves a figure being divided into mirror-image halves by a line, whereas rotational symmetry involves rotating the figure around a point, and at certain angles, the figure looks exactly the same.
How can I check if a shape has line symmetry?

+
You can check for line symmetry by drawing a line through the shape or object. If you can fold the shape along this line and both sides match perfectly, the shape has line symmetry along that line.
Is it possible for a shape to have both line and rotational symmetry?

+
Yes, many shapes, particularly regular polygons like squares and equilateral triangles, exhibit both types of symmetry. They have lines of symmetry and can also be rotated to match their original orientation multiple times within a 360-degree rotation.