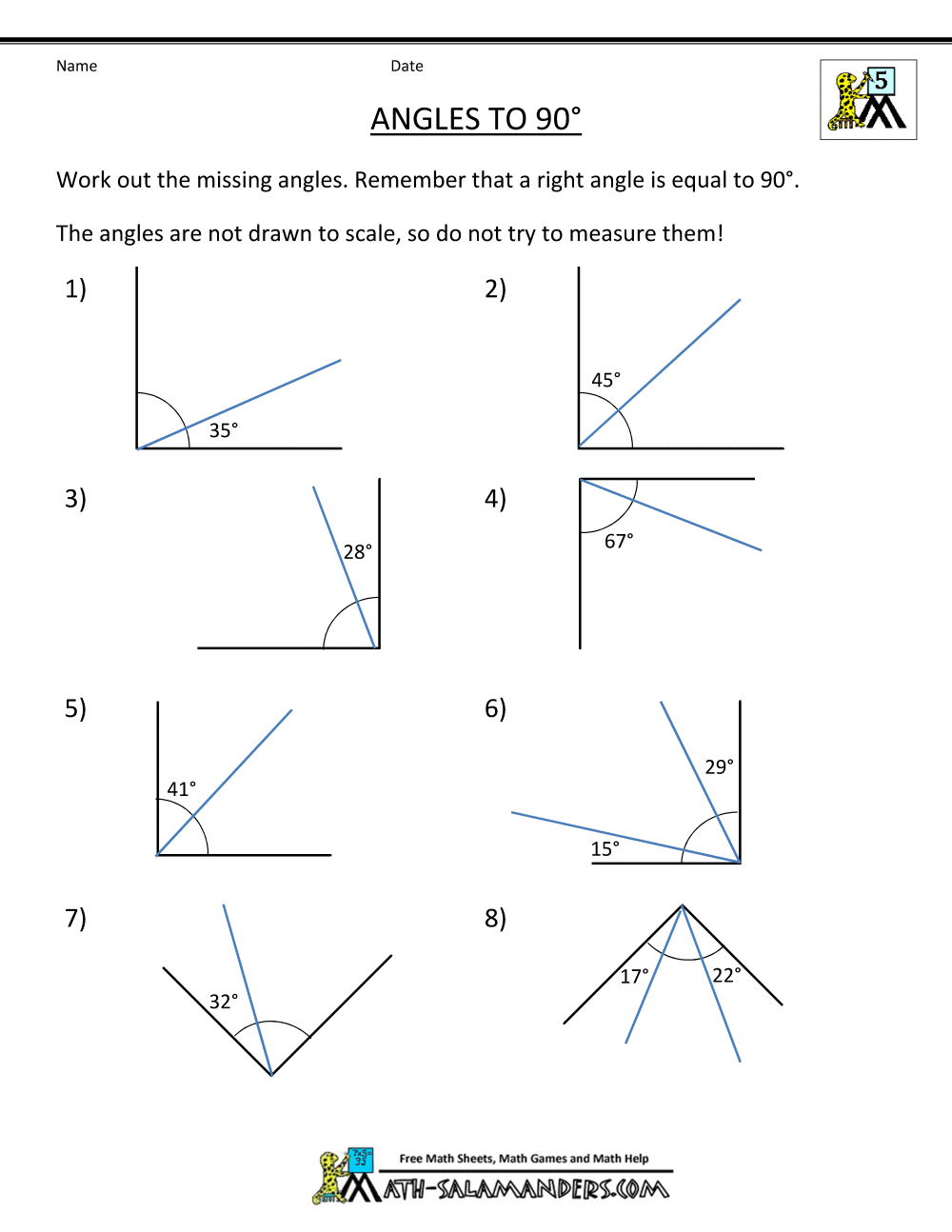
Geometry 5.3 Worksheet: Simplified Answers and Explanations

In today's educational landscape, mastering geometry is essential not only for academic success but also for developing a deeper understanding of the spatial world around us. Geometry Chapter 5.3 often introduces students to midsegments, bisectors, and the triangle midsegment theorem. This blog post aims to break down this section, providing simplified answers and explanations to common problems encountered in Geometry 5.3 worksheets. Here's how you can navigate through the complexities of these geometric concepts with ease.
Understanding Midsegments

At the heart of Geometry Chapter 5.3 lies the concept of midsegments. These are segments that join the midpoints of two sides of a triangle. Here’s what you need to know:
- Midsegment Theorem: A midsegment of a triangle is parallel to the third side and half its length.
- Properties:
- It divides the triangle into two smaller triangles that are similar to the original.
- The midsegment creates four triangles within the original triangle, all congruent to each other.
Example Problem: If the midsegment of a triangle is 5 units long, how long is the base of the triangle parallel to this midsegment?
| Step | Action | Result |
|---|---|---|
| 1 | Use the Midsegment Theorem | Midsegment is half the length of the parallel side |
| 2 | Multiply the midsegment by 2 | 5 units * 2 = 10 units |

Perpendicular Bisectors

The perpendicular bisector is a line that divides a segment into two equal parts, perpendicular to the segment itself. Here’s how you can work with it:
- Properties of Perpendicular Bisectors:
- Every point on the perpendicular bisector is equidistant from the endpoints of the segment it bisects.
- In a triangle, the three perpendicular bisectors intersect at the circumcenter, the center of the circle passing through all three vertices.
Example Problem: Given that point P is on the perpendicular bisector of segment AB, find PA if PB = 7 units.
| Step | Action | Result |
|---|---|---|
| 1 | Understand the property | PA = PB because P is on the perpendicular bisector |
| 2 | Directly state the result | PA = 7 units |
The Triangle Midsegment Theorem in Action
The triangle midsegment theorem not only applies to basic geometry but also has real-world applications. Here’s how:
- Real-World Application: Imagine you’re a surveyor trying to determine the distance across a river without crossing it. You can use the midsegment theorem to estimate the width:
| Step | Action | Result |
|---|---|---|
| 1 | Identify points A and B on opposite sides of the river | Points identified |
| 2 | Measure the distance from A to C, where C is the midpoint of the river’s path | Distance AC measured |
| 3 | Use the midsegment theorem to double the distance from A to C | Distance AB = 2 * AC |
👀 Note: Understanding midsegments can greatly simplify complex measurements in real-world applications like architecture and surveying.
Concluding Remarks

Geometry Chapter 5.3 introduces students to fundamental concepts that not only enhance their mathematical capabilities but also provide practical tools for solving everyday problems. By understanding midsegments, perpendicular bisectors, and the triangle midsegment theorem, you are equipped to tackle not only academic questions but also real-world scenarios that require spatial reasoning. Keep practicing these concepts, and you’ll find that geometry becomes not just a subject to study, but a lens through which to see and understand the world better.
What is the importance of the midsegment theorem in geometry?
+
The midsegment theorem provides a direct relationship between the sides of a triangle, making it easier to calculate unknown lengths or confirm properties of triangles, especially in applications like architecture and surveying.
How does one find the perpendicular bisector?
+
To find the perpendicular bisector of a line segment, you can either use the midpoint formula to calculate the midpoint and then find the slope perpendicular to the line segment or construct it geometrically by folding the paper such that the endpoints of the segment meet.
Can the midsegment theorem be applied to any polygon?

+
While the midsegment theorem is most commonly discussed for triangles, similar principles can be applied to other polygons to understand their symmetry and properties, although with more complex calculations.