Geometry 1.2 Worksheet: Segments, Bisectors, Midpoints Answers

In high school geometry, understanding the properties of line segments, bisectors, and midpoints forms a foundational aspect of spatial thinking. This blog post is designed to help students navigate through the nuances of the Geometry 1.2 Worksheet, focusing on segments, bisectors, and midpoints. These concepts not only aid in solving geometric problems but also enhance logical reasoning.
What is a Line Segment?


A line segment is a part of a line with two definite endpoints. Here's what you need to know:
- Endpoints: These are the points where the segment starts and ends.
- Length: The distance between the endpoints.
📝 Note: All points on a line segment lie on the same straight line.
Understanding Bisectors

A bisector divides something into two equal parts. Here are the key points:
- Line Segment Bisector: A line, ray, or segment that splits another segment into two congruent parts.
- Perpendicular Bisector: A line that not only bisects but is also perpendicular to the segment.
| Bisector Type | Description |
|---|---|
| Angle Bisector | Divides an angle into two equal angles. |
| Perpendicular Bisector | Divides a segment into two equal parts and meets the segment at a right angle. |

✅ Note: Perpendicular bisectors are useful in constructing geometric shapes with high accuracy.
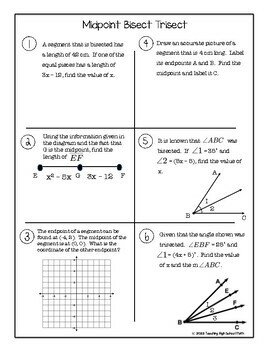
Exploring Midpoints
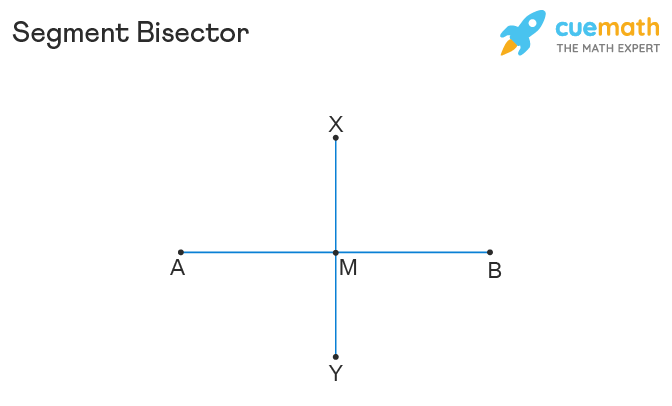
The midpoint of a line segment is the point halfway between the endpoints. Here are some essential facts:
- Location: The midpoint is equidistant from both endpoints.
- Calculation: You can find it using the midpoint formula: (x1+x2)/2 , (y1+y2)/2.

💡 Note: The midpoint theorem states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half as long.
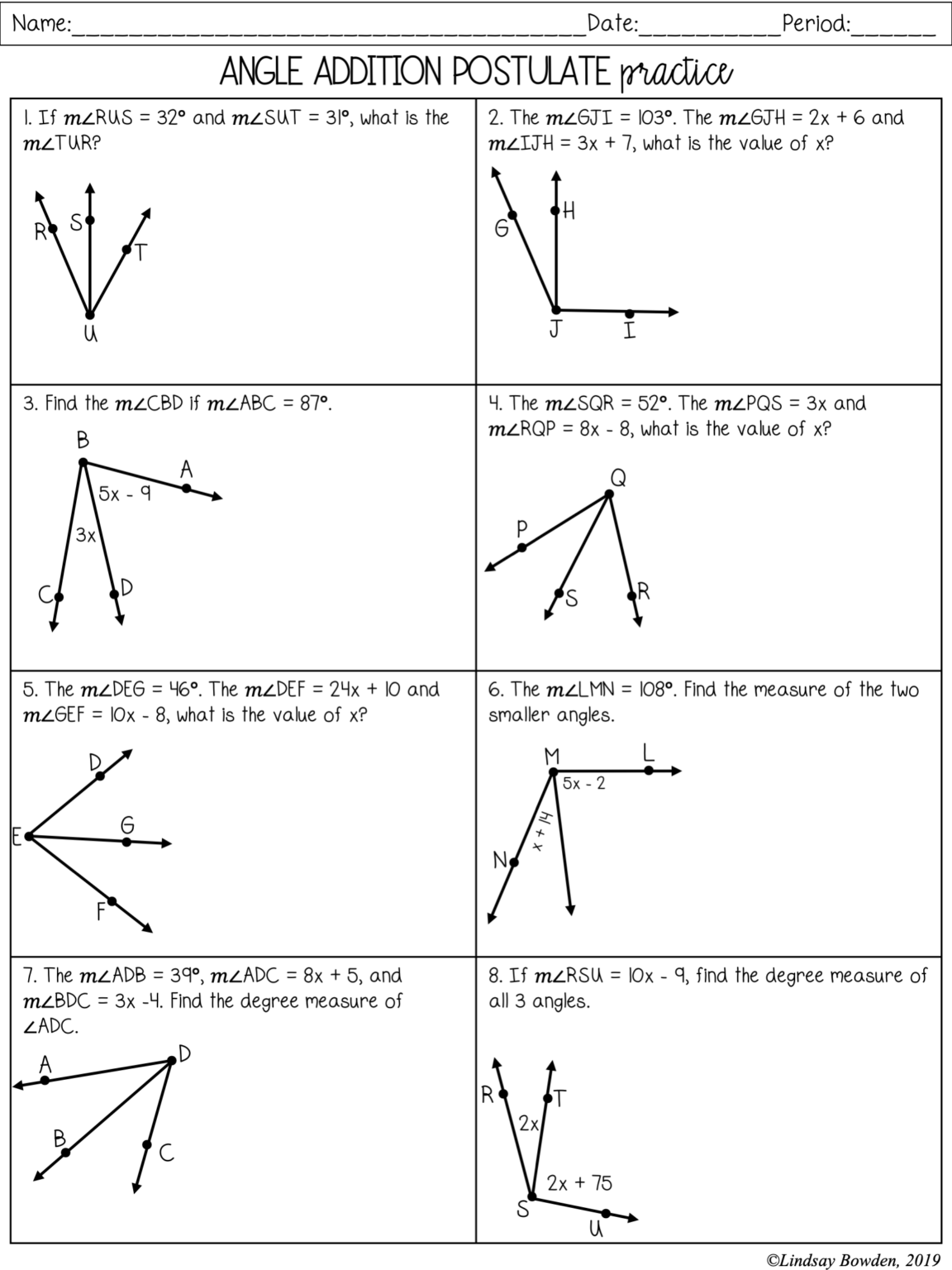
Practical Applications in Geometry Worksheets

When working on Geometry 1.2 worksheets, understanding these elements allows you to:
- Solve problems involving distances and divisions of segments.
- Construct and analyze geometric shapes with precision.
- Understand and apply theorems related to midpoints and bisectors.
Steps to Find Midpoints

Here’s a step-by-step guide:
- Identify the coordinates: Determine the (x1,y1) and (x2,y2) for the endpoints of the segment.
- Calculate: Apply the midpoint formula to find the (x, y) coordinate of the midpoint.
Common Mistakes to Avoid

Students often:
- Forget to include both x and y coordinates when calculating midpoints.
- Confuse bisectors with perpendicular lines, not understanding that the angle of intersection matters.
⚠️ Note: Double-check your calculations and remember that geometry is about precision.
Enhancing Your Skills
To get better at these geometric concepts:
- Practice with various worksheet problems.
- Use geometric software or apps for dynamic visualization.
- Engage in discussions with peers or teachers to clarify any doubts.
Understanding segments, bisectors, and midpoints not only helps in geometry but also in subjects like trigonometry and algebra. These principles provide a solid foundation for spatial analysis, measurement, and even design.
How can I find the length of a segment without measuring?
+
Use the distance formula: sqrt((x2-x1)^2 + (y2-y1)^2). This formula calculates the Euclidean distance between two points.
What is the difference between a line segment, a line, and a ray?
+
A line extends infinitely in both directions, a ray extends infinitely in one direction from its endpoint, and a line segment has two endpoints and does not extend infinitely.
Why are perpendicular bisectors important in triangles?

+
Perpendicular bisectors of the sides of a triangle intersect at the triangle's circumcenter, which is equidistant from all vertices. This point helps in constructing circumcircles and analyzing symmetry in triangles.
The principles of geometry extend beyond the worksheets and into the world around us. Whether you’re designing buildings, creating art, or simply organizing space in everyday life, an understanding of segments, bisectors, and midpoints proves invaluable. This post has aimed to solidify your grasp on these concepts, ensuring you’re well-equipped to tackle your Geometry 1.2 assignments with confidence. Keep practicing, visualizing, and questioning, as geometry is not just about solving problems but about shaping your understanding of the world in a structured way.