Master Geometry with Our Fun Geometric Proofs Worksheet
The Importance of Geometric Proofs in Math Education

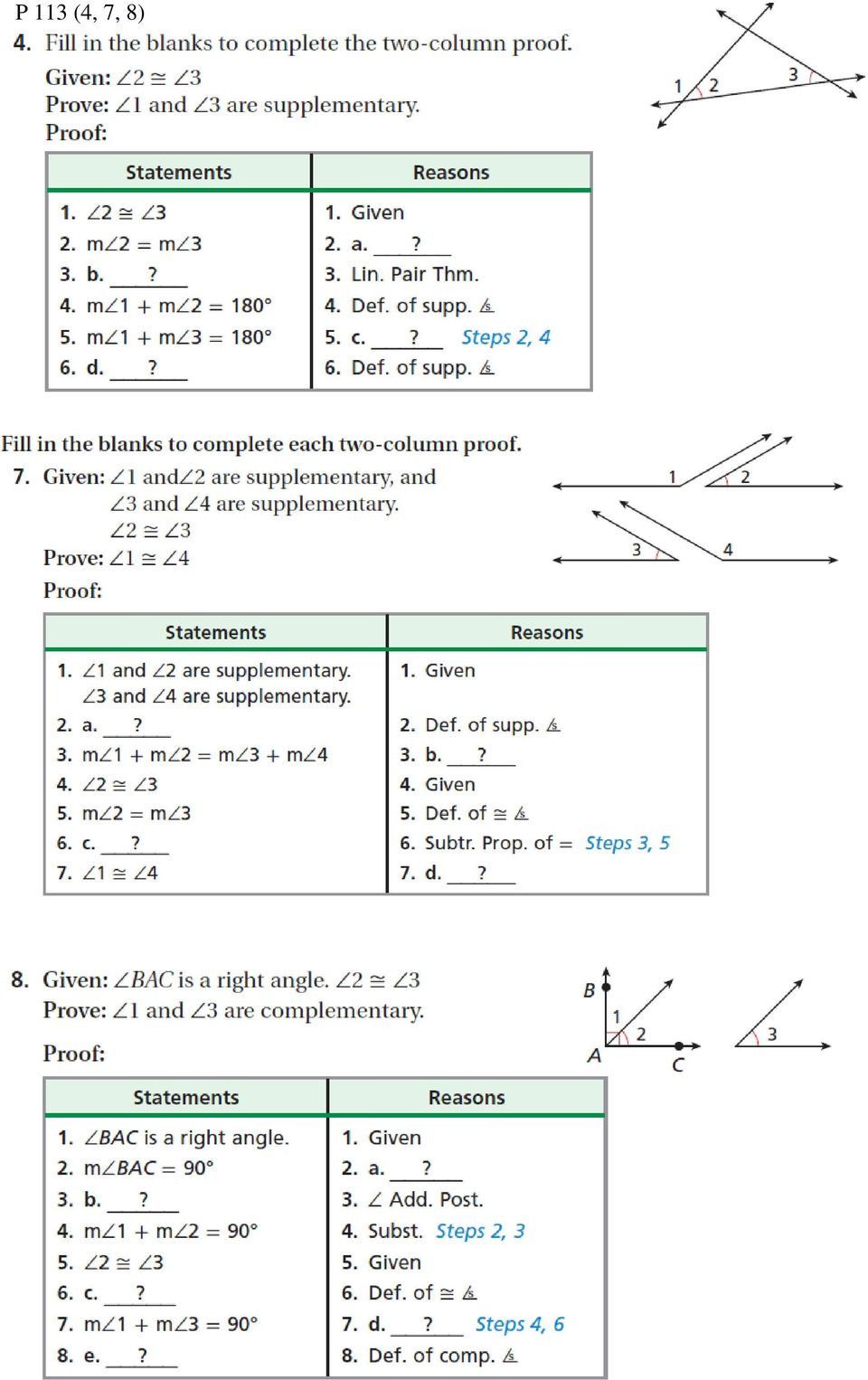
Geometry, often dubbed the visual language of mathematics, provides students with an unparalleled opportunity to develop logical reasoning, critical thinking, and problem-solving skills. At the heart of this subject lies geometric proofs, a method that not only validates geometric theorems but also serves as a cornerstone in understanding the structure and certainty of mathematics. Engaging with our fun geometric proofs worksheet can significantly enhance your grasp of these fundamental concepts, making learning both effective and enjoyable.
Understanding Geometric Proofs

Before diving into the worksheets, let’s ensure we have a clear understanding of what geometric proofs are:
- Definition: A geometric proof is a logical argument that uses deductive reasoning to establish the truth of a statement or theorem in geometry. It involves constructing a series of statements supported by known axioms, definitions, and previously proven theorems.
- Elements of Proofs:
- Given: The initial information provided as a fact.
- To Prove: The statement or theorem you aim to establish.
- Steps: The logical, sequential steps you take to arrive at the conclusion.
- Justifications: Reasons or theorems supporting each step.
- Types of Proofs:
- Direct Proof: Proving by directly connecting given statements to the desired conclusion.
- Indirect Proof: Proving by showing that the negation of the theorem leads to a contradiction.
- Proof by Contradiction: Similar to indirect proof but focuses on the contradiction itself.
Why Use Worksheets for Learning Geometric Proofs?

The benefits of using geometric proofs worksheets are multifaceted:
- Structured Learning: Worksheets provide a step-by-step approach to learning, breaking complex proofs into manageable segments.
- Practice and Repetition: Repetitive practice is key in mastering the art of logical deduction, which geometric proofs demand.
- Engagement and Fun: Well-designed worksheets can make geometry fun, engaging students with puzzles, visual elements, and real-world applications.
- Self-Assessment: Worksheets allow students to test their understanding, identify areas needing improvement, and self-correct.
Features of Our Fun Geometric Proofs Worksheet

Our worksheet is designed to transform learning geometry into an exciting journey:
- Visual Aids: Use of diagrams and puzzles to illustrate geometric problems.
- Themed Sections: Proofs are themed around real-life scenarios, from architecture to art, making learning relevant and interesting.
- Multiple Levels: Progressively challenging levels from basic to advanced proofs cater to different learning stages.
- Hints and Examples: Embedded hints guide students without giving away the solution, fostering independent problem-solving.
- Answer Keys: Detailed step-by-step solutions allow students to check their work and understand the thought process involved.
How to Use the Worksheet Effectively

Here are some tips to maximize your learning with our fun geometric proofs worksheet:
- Set Goals: Define what you want to achieve with each session—e.g., mastering a specific type of proof or improving your proof writing skills.
- Start with the Basics: Begin with fundamental proofs to build a solid foundation before tackling more complex problems.
- Understand Each Step: Don’t rush through. Understand why each step of the proof is necessary and what each justification means.
- Use Visual Aids: Sketch and label diagrams to visualize the geometric properties and relationships you are proving.
- Collaborate: Discuss proofs with peers or teachers. Sometimes explaining your thought process can solidify your understanding.
- Check Your Work: After attempting a proof, use the provided solutions to check for accuracy, noting where mistakes occurred and learning from them.
🚨 Note: While the worksheet provides a structured approach, remember that understanding proofs also requires thinking outside the box and exploring different methods.
The Impact of Learning Geometric Proofs

Engaging with geometric proofs has profound benefits:
- Enhanced Logical Thinking: Students develop a rigorous method of thought, applicable in various fields of study and real-life problem-solving.
- Preparation for Higher Math: Proficiency in proofs is crucial for advanced mathematics, including calculus, linear algebra, and beyond.
- Career Relevance: Fields like engineering, architecture, computer science, and even philosophy require logical deduction and proof-based reasoning.
- Academic Success: Improved performance in math exams, where proofs are often a major component.
- Confidence and Perseverance: Overcoming complex proofs builds confidence, resilience, and a deeper appreciation for mathematics.
How often should I use the geometric proofs worksheet?

+
Engage with the worksheet regularly, at least 2-3 times a week. Consistency is key in developing your proof-solving skills.
What if I'm stuck on a proof?

+
Don't panic. Use the hints provided, sketch diagrams, or step back to gain a new perspective. Sometimes, discussing the problem with someone else can also help.
Are there any other resources to help with geometric proofs?

+
Yes, textbooks, online tutorials, and math forums can provide additional insights and practice. Our worksheet also includes references to external resources for further study.
Can this worksheet help with competitive math?

+
Absolutely. The worksheet covers essential proof techniques that are often tested in competitions, helping you sharpen your competitive edge.
How can parents or teachers utilize this worksheet effectively?

+
By integrating it into lesson plans, providing guided practice sessions, and encouraging collaborative learning to discuss and develop proofs together.
In wrapping up, understanding geometric proofs through our engaging worksheet transforms the learning experience from routine to revelatory. By mastering the art of proving mathematical statements, students not only improve in geometry but also enhance their cognitive skills and academic preparedness. This foundational approach paves the way for a deeper appreciation of the world through the lens of logical reasoning and order. With dedication, practice, and the right tools, geometric proofs become not just a challenge to overcome, but a journey of discovery and empowerment in the realm of mathematics.



