5 Proven Geometric Proof Practice Strategies

Embarking on the journey of mastering geometric proofs can be both exhilarating and challenging. Geometry is not just about shapes; it's about logical reasoning, where each step builds upon the previous one. This article will guide you through five proven strategies to enhance your practice in geometric proofs, ensuring that your skills in this foundational math subject grow robustly.
Understanding the Basics

Before diving into complex proofs, ensuring you have a solid grasp of the foundational elements of geometry is crucial. Here are key areas to focus on:
- Definitions: Know your terms. Understanding definitions like 'line', 'angle', 'triangle', etc., is fundamental.
- Axioms and Postulates: These are the building blocks of proofs. Familiarize yourself with common axioms like the Parallel Postulate or the Congruence Postulates.
- Properties and Theorems: Properties of shapes and theorems that have already been proven provide you with the tools for your proofs.

Key Geometric Definitions

| Term | Definition |
|---|---|
| Line | A straight path extending infinitely in both directions. |
| Angle | The space (usually measured in degrees) between two intersecting lines or surfaces at or close to the point where they meet. |
| Triangle | A three-sided polygon with the sum of its angles equal to 180 degrees. |

Strategy 1: Master Diagramming

Visualizing geometric problems through diagrams is a pivotal step:
- Use clear labels for all points, lines, and angles. This clarity aids in both understanding and demonstrating the proof.
- Mark angles with arcs and arcs with ticks to indicate equal measures.
- Draw supplementary or auxiliary lines when needed to reveal hidden relationships or properties.
📝 Note: Always ensure your diagram reflects the problem's conditions accurately; a small error can lead to an incorrect proof.

Strategy 2: Apply Logical Reasoning

Logical reasoning is the backbone of every proof:
- Start with what you know (given information) and use theorems, definitions, and logical steps to lead to the proof.
- Think in both directions: from what you're trying to prove back to the givens.
- Identify and work with conditional statements effectively.
🧠 Note: Geometry often involves indirect proof or proof by contradiction, where you assume the opposite of what you want to prove and show this leads to an absurdity.
Strategy 3: Practice Diverse Problem Sets

Practicing diverse problems not only broadens your knowledge but also exposes you to different proof techniques:
- Work through problems from various geometry textbooks or online resources.
- Participate in competitions or workshops for an added challenge and insights.
- Review problems to understand where you went wrong or to find alternative proof methods.
🔍 Note: Diversity in problems helps to encounter different geometric relationships and learn how to apply theorems in various scenarios.
Strategy 4: Work Backwards from Solutions

Understanding proofs from a finished solution can provide a template:
- Review the logical steps that were taken to arrive at the solution.
- Try to reconstruct the proof in your own words or with your own approach.
- Focus on understanding the critical steps that made the proof work.
📚 Note: By analyzing completed proofs, you learn to recognize the structural elements common to many geometric proofs.
Strategy 5: Utilize Proof Techniques
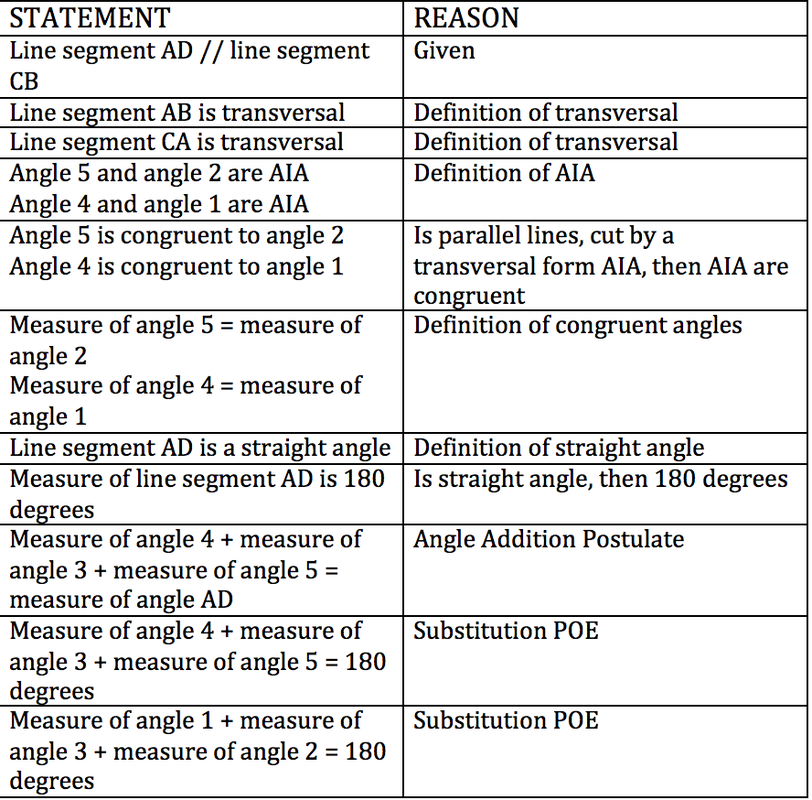
Each proof technique has its time and place:
- Direct Proof: Proving a statement by showing that the premises logically lead to the conclusion.
- Proof by Contradiction: Assume the opposite and show it leads to a contradiction.
- Proof by Induction: Useful in proving statements about sequences or infinite series.
- Two-Column Proofs: Using statements on one side and reasons on the other.
🛠️ Note: Different problems require different proof techniques. Master them all to have the right tools for any problem.
As you wrap up this exploration into geometric proof strategies, remember that practice is the key. Building upon your foundational knowledge, visualizing through diagramming, sharpening your logical reasoning, and embracing various problem types will guide you towards mastering geometric proofs. By understanding and applying these strategies, you'll find yourself not just solving problems but appreciating the intricate beauty of geometry. Geometry proofs are not just a mathematical exercise but an intellectual journey where each step brings you closer to understanding the fundamental principles of the world around us.
Why are geometric proofs important in mathematics?

+
Geometric proofs are essential because they teach logical reasoning, critical thinking, and problem-solving skills. They also provide a rigorous way to validate geometric theorems, ensuring that what we learn about shapes and relationships is universally true.
Can geometric proofs be done differently?

+
Yes, there often isn’t just one correct way to prove a geometric theorem. Different students might come up with different proofs using varying methods or approaches. However, the logical steps must lead to the conclusion without gaps or leaps in logic.
How can I check if my geometric proof is correct?

+
You can check your proof by:
- Tracing each step back to the initial givens.
- Ensuring no steps are skipped or assumed without reason.
- Testing your proof with a specific case or example to see if it holds true.
- Comparing it with alternative proofs or solutions provided in textbooks or by teachers.
What are some common mistakes in geometric proofs?
+
Common mistakes include:
- Using undefined terms or assuming facts that need proof.
- Misapplying theorems or properties.
- Failing to label the diagram correctly or assuming what isn’t given.
- Not clearly stating the reason for each step or jumping to conclusions without a logical bridge.
How can I improve my speed in solving geometric proofs?
+
To increase your speed:
- Practice regularly to build intuition.
- Develop a habit of reading the problem quickly to understand the givens and the goal.
- Work on recognizing common proof structures and patterns.
- Learn to avoid unnecessary details and focus on key steps that lead to the proof.