5 Essential Tips for Solving Algebra 1 Functions
Algebra 1, often the first formal introduction to algebraic concepts in high school, can be both exciting and challenging. A significant part of this curriculum involves functions, which are fundamental to more advanced mathematical understanding. Here are five essential tips to help you grasp and solve problems related to Algebra 1 functions effectively.
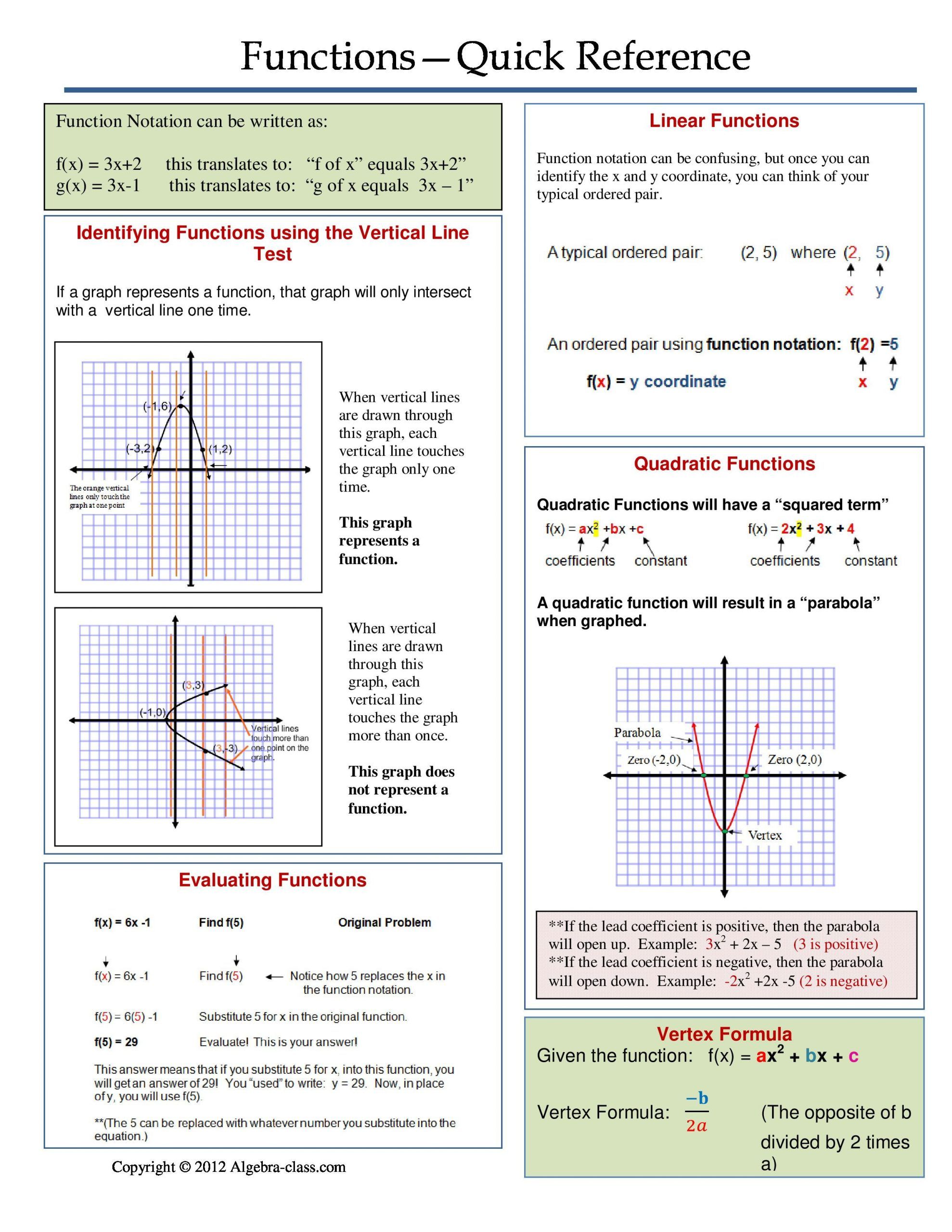
Understand the Concept of Functions

Before diving into specifics, it’s crucial to understand what a function is. In simple terms, a function is a rule that assigns each element from a set, called the domain, to exactly one element of another set, known as the range.
- A function can be visualized using input-output tables or graphs.
- Functions can be represented in various forms like equations, tables, or graphs, making them versatile tools in algebra.
Learn to Recognize Common Types of Functions

Algebra 1 introduces several key types of functions:
| Function Type | Description |
|---|---|
| Linear Functions | Their graph forms a straight line, often represented as f(x) = mx + b, where m is the slope, and b is the y-intercept. |
| Quadratic Functions | Characterized by a parabolic curve, their standard form is f(x) = ax² + bx + c. They can model phenomena like projectile motion. |
| Exponential Functions | Describes rapid growth or decay, represented as f(x) = ab^x, where b is the base, a is a constant, and x is the exponent. |

Master the Vocabulary and Notation

Understanding function notation and vocabulary is pivotal for solving algebra problems:
- f(x) denotes the output of the function for input x.
- Terms like domain, range, input, output, independent variable, and dependent variable should be clearly understood.
📘 Note: The clarity in notation often helps in solving equations more efficiently. Knowing how to read and write functions is essential for any algebraic operation.
Practice Graphing Functions

Graphing is not just about plotting points; it’s about understanding the behavior of functions:
- Plot key points: Intercepts, maximums, or minimums can provide significant insight.
- Understand the transformations: Learn how changes in equation affect the graph (e.g., shifting, stretching, compressing, or reflecting).
Solve Problems Methodically

When tackling function-related problems, adopt a systematic approach:
- Identify the type of function: Knowing if it’s linear, quadratic, or exponential will guide your solution strategy.
- Use algebraic manipulation: Solve for variables by applying algebraic rules like distributing, factoring, or using square roots.
- Graphically solve: Sometimes, plotting the function might give you visual cues to solve complex problems.
In summary, understanding Algebra 1 functions requires a blend of conceptual knowledge, recognition of function types, mastering of notation, graphical interpretation, and problem-solving skills. Each of these tips will bolster your understanding and proficiency in dealing with functions, laying a solid foundation for higher-level math courses. Continually practicing these techniques will not only increase your fluency but also your confidence in tackling algebra problems.
What is the difference between a function and an equation?

+
An equation states that two expressions are equal, whereas a function defines a relationship where each input has exactly one output. Equations can represent multiple solutions or none, while functions must have a unique output for each input.
How can I tell if a graph is a function?

+
Use the vertical line test: if any vertical line drawn on the graph intersects the graph at more than one point, then the graph does not represent a function.
What are some common mistakes when dealing with functions?

+
Frequent errors include:
- Confusing f(x) with multiplication or variable names like fx.
- Misinterpreting domain and range restrictions.
- Not accounting for transformations when graphing functions.
- Miscalculating function values by overlooking rules like order of operations or failing to substitute correctly.