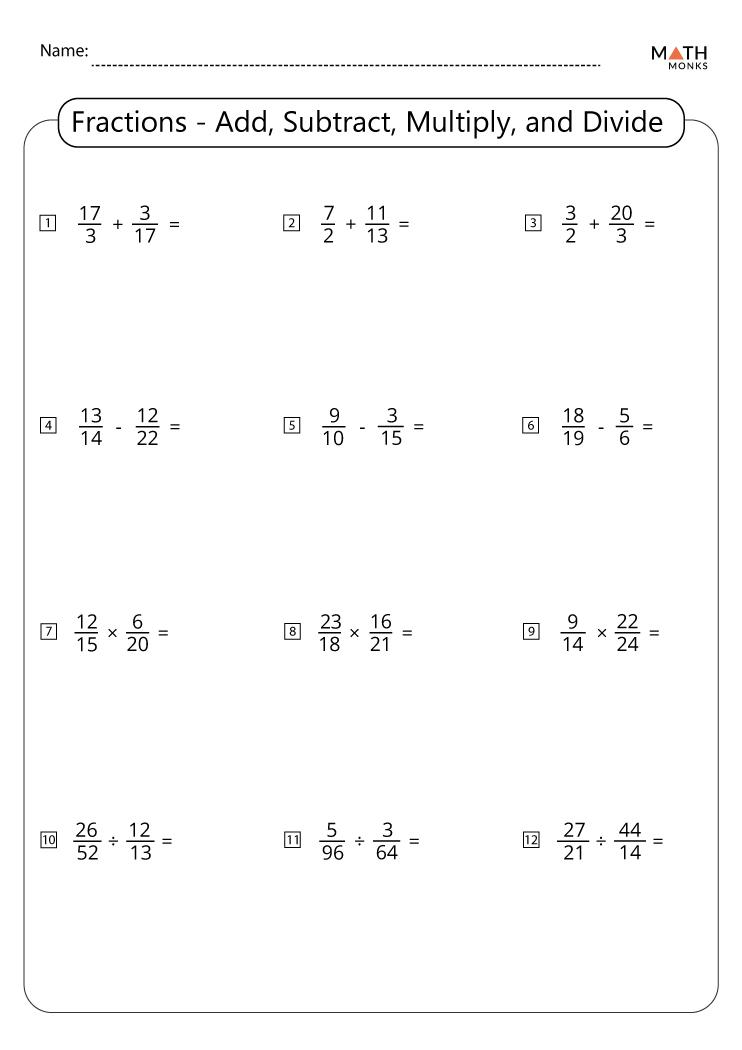
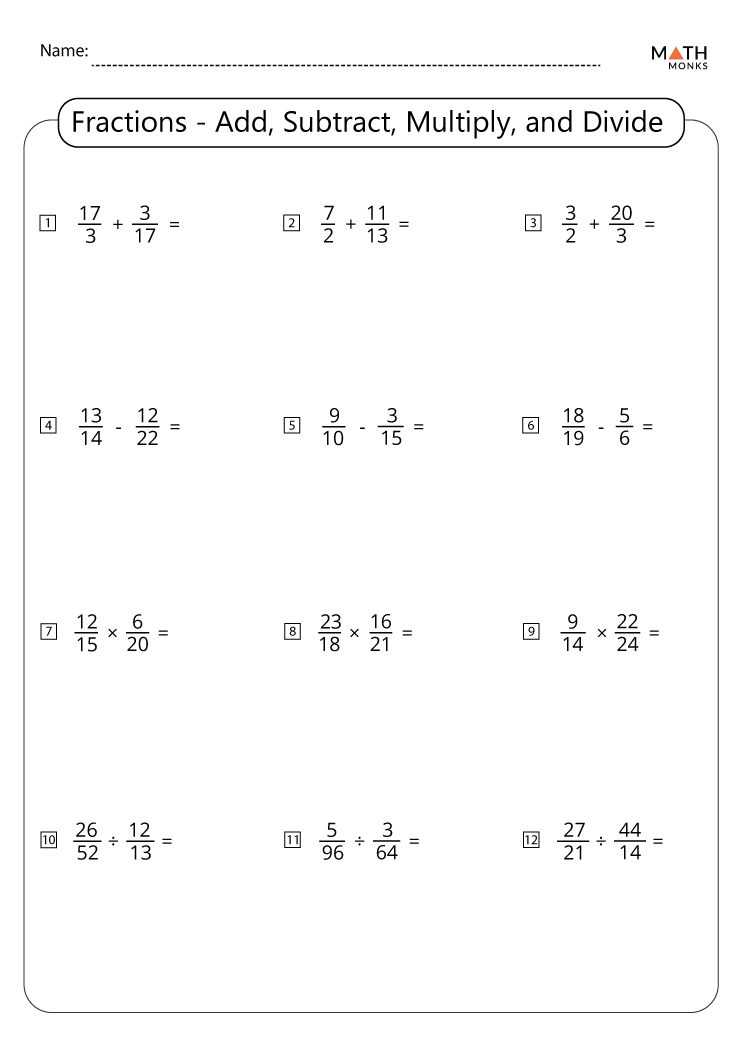
Mastering Fractions: Add, Subtract, Multiply, Divide with Ease

Learning to work with fractions is essential, not just in math classes but also in everyday scenarios, such as cooking, baking, or dealing with measurements. Fractions can initially seem daunting due to their unique nature, but with a systematic approach, you can master them effortlessly. This post will guide you through the basic operations on fractions: addition, subtraction, multiplication, and division.
Understanding Fractions

Before diving into operations, let's clarify what a fraction represents. A fraction consists of:
- Numerator: The top number, indicating how many parts you have.
- Denominator: The bottom number, showing how many parts the whole is divided into.
Here's a table illustrating different types of fractions:
| Fraction Type | Example |
|---|---|
| Proper Fraction | 1/4 (numerator < denominator) |
| Improper Fraction | 5/4 (numerator > denominator) |
| Mixed Number | 1 1/4 (an integer part plus a proper fraction) |

Adding and Subtracting Fractions

Step-by-Step Guide to Adding Fractions

- Find a common denominator: To add or subtract fractions, they must have the same denominator.
- Adjust each fraction: Multiply both the numerator and denominator of each fraction by the same factor so their denominators become the common one.
- Sum the numerators: Add the adjusted numerators together.
- Form the new fraction: Place the sum of the numerators over the common denominator.
Example:

Let's add 1/3 and 1/6.
- Common denominator: 6
- Adjust 1/3: (1 x 2)/(3 x 2) = 2/6
- Sum numerators: 2/6 + 1/6 = 3/6
- Reduce: 3/6 simplifies to 1/2
🔍 Note: Always simplify your fraction by dividing both the numerator and denominator by their greatest common divisor (GCD).
Subtraction of Fractions

The process for subtraction is similar to addition:
- Find a common denominator.
- Adjust the fractions if necessary.
- Subtract the numerators.
- Form and simplify the new fraction.
Multiplying Fractions

How to Multiply Fractions:
- Multiply numerators together.
- Multiply denominators together.
- Convert the resulting product into a mixed number if necessary and simplify.
Example:

Let’s multiply 3⁄4 and 2⁄5:
- Multiply numerators: 3 x 2 = 6
- Multiply denominators: 4 x 5 = 20
- Result: 6⁄20
- Simplify: 6⁄20 simplifies to 3⁄10
Dividing Fractions

Dividing by a Fraction:

Dividing by a fraction means multiplying by its reciprocal (flipping the fraction):
- Find the reciprocal of the divisor (the fraction you’re dividing by).
- Multiply the dividend (the first fraction) by the reciprocal.
- Simplify if needed.
Example:
Divide 3⁄4 by 2⁄3:
- Reciprocal of 2⁄3 is 3⁄2.
- Multiply: (3⁄4) * (3⁄2) = 9⁄8
- Convert to mixed number: 1 1⁄8
Dealing with Mixed Numbers

Mixed numbers combine whole numbers with fractions. Here’s how to handle them during operations:
- Conversion to Improper Fraction: Multiply the whole number by the denominator, then add the numerator. Place the result over the denominator.
- Perform the Operation: Use the improper fraction in your calculation as explained above.
- Convert Back: If necessary, convert the result back to a mixed number.
Example:

Let’s add 2 3⁄5 and 1 4⁄7:
- Convert to improper fractions: 2 3⁄5 = 13⁄5, 1 4⁄7 = 11⁄7
- Find a common denominator (35):
- Adjust: 13⁄5 = 91⁄35, 11⁄7 = 55⁄35
- Add: 91⁄35 + 55⁄35 = 146⁄35
- Convert back: 4 6⁄35
⚠️ Note: Always double-check your work when dealing with mixed numbers to ensure accuracy.
In our exploration of mastering fractions, we’ve seen how straightforward processes can turn intimidating tasks into manageable ones. With practice, adding, subtracting, multiplying, and dividing fractions will become second nature, enabling you to confidently tackle more complex mathematical problems or everyday tasks involving fractions. Remember, each operation follows a set of rules that, once learned, can be applied almost instinctively. Keep practicing, and you’ll find that fractions aren’t the complex hurdle they once seemed.
What is the easiest way to find the common denominator?

+
The easiest way often involves finding the Least Common Multiple (LCM) of the denominators of the fractions. This method ensures the common denominator is as small as possible, simplifying the computation process.
Can I add fractions with different denominators without converting?

+
No, you must convert fractions to have a common denominator before adding or subtracting. This is the standard procedure to ensure accurate results.
What’s the importance of simplifying fractions?
+
Simplifying fractions reduces them to their lowest terms, making them easier to work with, understand, and compare. It’s essential for clarity and efficiency in mathematical operations.
How do I know if a fraction needs to be converted to a mixed number?
+
If the numerator of the fraction is greater than or equal to the denominator, it should be expressed as a mixed number for practical purposes or to reflect the whole number part clearly.
Why does the process of dividing by a fraction involve multiplication?
+
Dividing by a fraction is equivalent to multiplying by its reciprocal, which reverses the effect of the original fraction, thus giving us the correct result of the division.