Convert Fractions to Decimals Easily With This Worksheet

Converting fractions to decimals might seem like a daunting task, especially when numbers aren't easily divisible. However, with the right approach and tools like a worksheet, this conversion can become an intuitive part of your mathematical toolkit. Whether you're a student looking to understand basic math concepts better or a teacher aiming to help others, this guide will walk you through every step with clarity and ease.
Why Convert Fractions to Decimals?

Converting fractions into decimals has a variety of practical applications in everyday life and mathematical education:
- Real-World Applications: Think about splitting a bill at a restaurant or calculating discounts during a sale. Decimal representations make these tasks easier.
- Mathematical Operations: Decimal forms simplify addition, subtraction, multiplication, and division when dealing with fractions.
- Standardization: Converting fractions to decimals brings uniformity, making numbers easier to compare and understand across various contexts.
Basic Concepts

Before we dive into using a worksheet to convert fractions, it's beneficial to understand some foundational concepts:
- Fraction: A way to express part of a whole or division.
- Decimal: A number represented in base 10 with a decimal point separating the whole number part from the fractional part.
- Long Division: A method where you divide one number (the dividend) by another (the divisor) to find how many times the divisor goes into the dividend, including decimal places if necessary.
🔔 Note: Understanding these concepts is vital because they provide the framework for all future conversions.
Step-by-Step Conversion Process

Here’s how you can convert any fraction to a decimal:
1. Divide the Numerator by the Denominator

The numerator (top number) becomes the dividend, and the denominator (bottom number) becomes the divisor.
2. Perform Long Division

Use long division to divide the two numbers. Here are the steps:
- Set up the division problem with the dividend inside the house (right).
- Begin by seeing how many times the divisor goes into the dividend, write that number on top, and multiply back to subtract from the dividend.
- Continue with the next digit from the dividend, bringing down a zero if needed.
- Keep dividing until you have the desired level of precision or until the division terminates or repeats.
Here's an example:
| Division | Step |
|---|---|
| 1 ÷ 2 = 0.5 | The division is straightforward here, resulting in 0.5 as the decimal. |
| 2 ÷ 3 = 0.6666… | Here, the division results in a repeating decimal: 0.6666... or often written as 0.6̅ |

🔔 Note: A repeating decimal indicates an infinite, non-terminating pattern. For simplicity, you can round up to the desired number of decimal places.
3. Interpret the Result

Look at the decimal result:
- If it terminates, like 0.5, you can easily express it as a decimal.
- If it repeats, like 0.6666..., you might indicate this with a dot over the last digit or use a bar over the repeating part.
- If you need a finite decimal, decide on the precision and round as necessary.
Using a Worksheet for Conversion
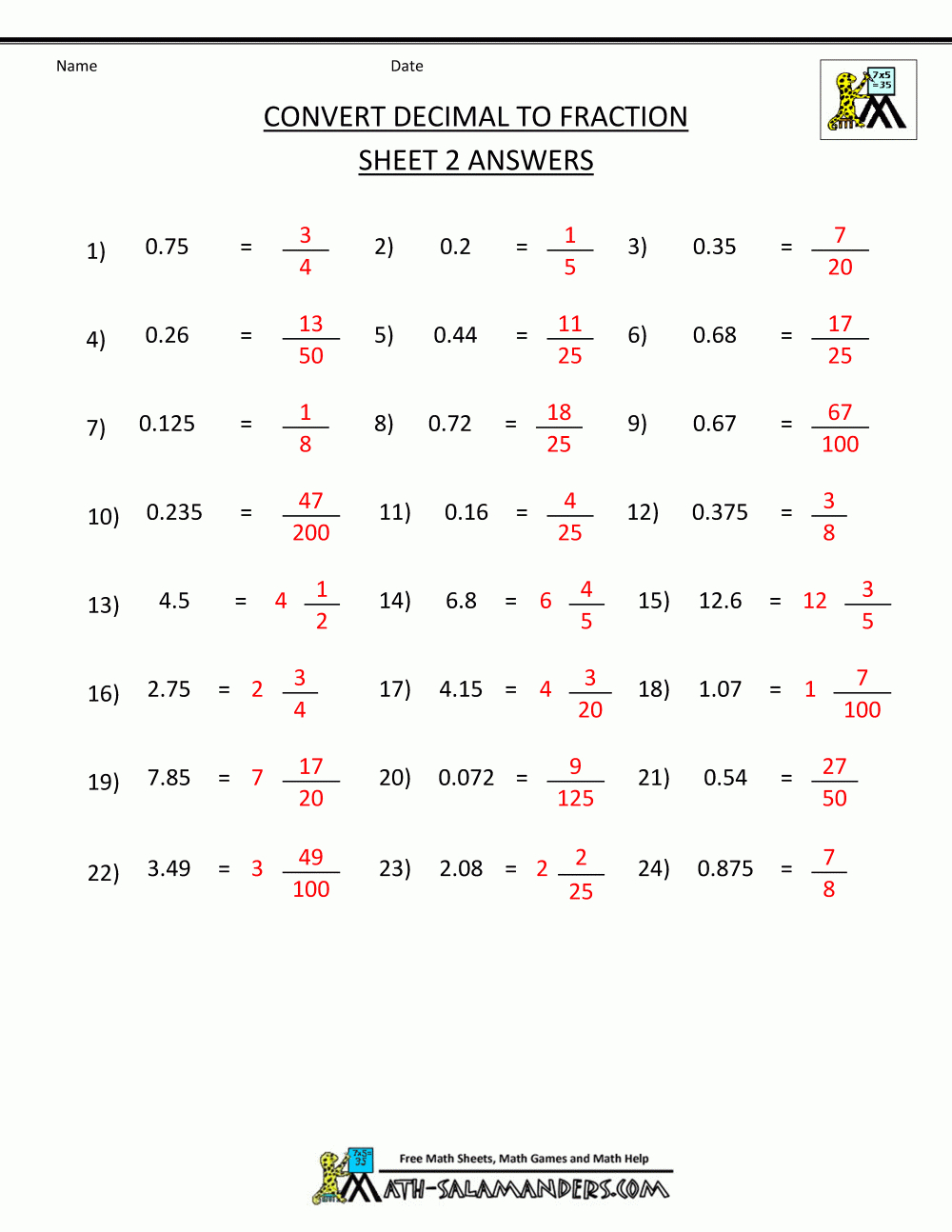
Converting fractions to decimals manually can be time-consuming, especially for complex numbers or large quantities. A worksheet designed specifically for this task streamlines the process:
Benefits of a Worksheet

- Organization: Helps keep the divisions organized, reducing errors.
- Practice: Provides a structured way to practice, improving speed and accuracy.
- Efficiency: Makes learning the process visually manageable.
How to Use the Worksheet

To utilize a worksheet for converting fractions to decimals:
- Identify the fractions: Write down the fractions you wish to convert.
- Set up the division: Use the worksheet to set up each long division problem. Ensure each section has space for the numerator (dividend) and the denominator (divisor).
- Perform the division: Divide according to the steps listed above, jotting down each step in the allocated space on the worksheet.
- Record the result: After division, record the decimal result on your worksheet.
🔔 Note: For repeating decimals, note down the repeating pattern or decide on a point of truncation for simplicity.
Advanced Techniques

While the basic method is effective, there are some tips and techniques that can make this process more efficient:
- Long Division Shortcuts: Learn shortcuts for division to speed up your calculations.
- Recognizing Patterns: Some fractions convert to well-known decimals (e.g., 1/3 = 0.3333...), so recognizing these can help.
- Estimating: In some cases, estimating the decimal value based on known benchmarks can be faster than exact division.
🔔 Note: Remember, understanding the underlying principles enhances efficiency in conversion but doesn't negate the need for practice with the worksheet.
In Summary

Converting fractions to decimals might initially appear complex, especially with non-terminating fractions. However, with structured practice using a well-designed worksheet, you can master this skill. By breaking down the process into steps and providing ample practice, you not only improve your ability to convert fractions to decimals but also understand mathematical concepts more deeply. Whether for academic purposes, personal knowledge, or professional requirements, the ability to effortlessly convert fractions to decimals is a valuable tool in your mathematical toolkit.
Why is it important to convert fractions to decimals?

+
Decimals simplify mathematical operations like addition and subtraction, making them easier in real-world scenarios like budgeting or scientific calculations where uniformity is key.
How can I tell if a fraction converts to a terminating or repeating decimal?

+
A fraction terminates if the denominator (after simplifying) only has 2s and 5s as prime factors. If there are other prime factors, the decimal repeats.
What should I do if a decimal keeps repeating?

+
When a decimal repeats, you can either round it to a desired number of decimal places or indicate the repetition with a dot over the repeating digit or a bar over the repeating pattern.