Mastering Fractions with Mixed Numbers Worksheet

Mastering Fractions with Mixed Numbers Worksheet

Understanding fractions and mixed numbers is an essential part of mathematics, and it’s crucial to have a solid grasp of these concepts to excel in various mathematical disciplines. Fractions represent a part of a whole, while mixed numbers combine a whole number with a fraction. In this worksheet, we will delve into the world of fractions and mixed numbers, exploring the concepts, rules, and problem-solving strategies.
What are Fractions?

Fractions are a way to represent a part of a whole. A fraction consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
For example, consider the fraction 3⁄4. In this case, the numerator is 3, indicating that we have 3 equal parts, and the denominator is 4, indicating that the whole is divided into 4 parts.
Mixed Numbers: Combining Whole Numbers and Fractions

Mixed numbers are a combination of a whole number and a fraction. They are used to represent a whole number and a fraction together. For instance, the mixed number 2 1⁄2 represents the whole number 2 and the fraction 1⁄2.
Key Concepts and Rules
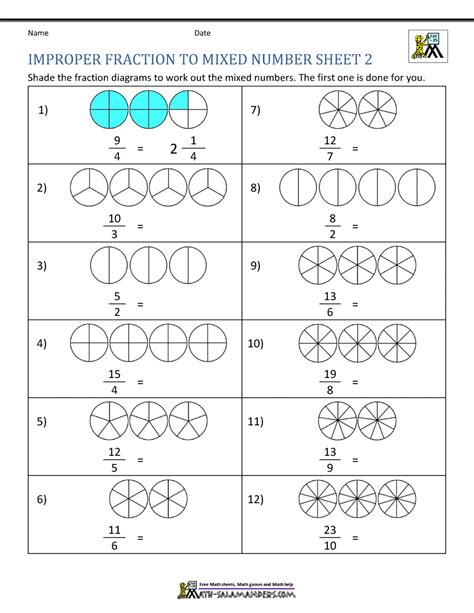
To master fractions with mixed numbers, you need to understand the following key concepts and rules:
- Equivalent Ratios: Two fractions are equivalent if they have the same value. For example, 1⁄2 = 2⁄4 = 3⁄6.
- Simplifying Fractions: Simplifying a fraction means reducing it to its simplest form. For example, 4⁄8 = 1⁄2.
- Adding and Subtracting Fractions: To add or subtract fractions, they must have the same denominator. For example, 1⁄4 + 1⁄4 = 2⁄4, while 1⁄4 - 1⁄4 = 0/4.
- Multiplying and Dividing Fractions: To multiply fractions, multiply the numerators and denominators separately. To divide fractions, invert the second fraction and multiply. For example, 1⁄2 × 3⁄4 = 3⁄8, while 1⁄2 ÷ 3⁄4 = 2⁄3.
- Converting between Fractions and Mixed Numbers: To convert a fraction to a mixed number, divide the numerator by the denominator. To convert a mixed number to a fraction, multiply the whole number by the denominator and add the numerator.
Worksheet Exercises

Now, let’s put these concepts into practice with some exercises!
Section 1: Simplifying Fractions
| Fraction | Simplified Fraction |
|---|---|
| 2⁄4 | ? |
| 3⁄6 | ? |
| 4⁄8 | ? |

Section 2: Adding and Subtracting Fractions
| Problem | Solution |
|---|---|
| 1⁄4 + 1⁄4 | ? |
| 2⁄4 - 1⁄4 | ? |
| 3⁄4 + 2⁄4 | ? |
Section 3: Multiplying and Dividing Fractions
| Problem | Solution |
|---|---|
| 1⁄2 × 3⁄4 | ? |
| 2⁄3 × 3⁄4 | ? |
| 1⁄2 ÷ 3⁄4 | ? |
Section 4: Converting between Fractions and Mixed Numbers
| Mixed Number | Fraction |
|---|---|
| 2 1⁄2 | ? |
| 3 3⁄4 | ? |
| 1 2⁄3 | ? |
Problem-Solving Strategies

When solving fraction problems, follow these steps:
- Read the problem carefully: Understand what is being asked and identify the key elements.
- Use visual aids: Draw diagrams or use number lines to help visualize the fractions.
- Simplify fractions: Simplify fractions to their simplest form before performing operations.
- Apply the rules: Use the rules of fractions to add, subtract, multiply, and divide.
- Check your work: Verify your answers by checking the equivalent ratios or simplifying the fraction.
📝 Note: Make sure to show your work and explain your reasoning when solving fraction problems.
Real-World Applications

Fractions and mixed numbers have numerous real-world applications, such as:
- Cooking: Measuring ingredients and scaling recipes.
- Building: Measuring materials and calculating quantities.
- Science: Measuring quantities and calculating ratios.
- Finance: Calculating interest rates and investment returns.
Conclusion

Mastering fractions with mixed numbers requires practice and a solid understanding of the key concepts and rules. By following the problem-solving strategies and applying the rules, you’ll become proficient in working with fractions and mixed numbers. Remember to simplify fractions, use visual aids, and check your work to ensure accuracy. With time and practice, you’ll become a pro at mastering fractions with mixed numbers!
What is the difference between a fraction and a mixed number?
+
A fraction represents a part of a whole, while a mixed number combines a whole number and a fraction.
How do I simplify a fraction?

+
To simplify a fraction, divide the numerator and denominator by the greatest common divisor (GCD).
Can I add or subtract fractions with different denominators?

+
No, fractions must have the same denominator to be added or subtracted.
Related Terms:
- Fractions mixed numbers worksheet pdf
- Mixed fraction worksheet with answers
- adding mixed number fractions sheet
- free mixed number fraction worksheets
- mixed fractions worksheets grade 7
- free printable mixed number worksheets



