Fractions and Decimals Worksheet: Boost Your Math Skills

In this comprehensive guide, we'll delve into the exciting world of fractions and decimals, which are fundamental concepts in mathematics. These number forms are essential for understanding more complex mathematical operations, for solving real-world problems, and they form the backbone of arithmetic proficiency. Whether you're a student looking to improve your math skills or a teacher aiming to help your students, this worksheet on fractions and decimals will provide a solid foundation to enhance your mathematical prowess.
Understanding Fractions

Fractions are part of the whole and consist of two parts: the numerator, which tells us how many parts are taken, and the denominator, which indicates the total number of equal parts the whole is divided into. Here are key points to understand fractions:
- Proper Fractions: The numerator is less than the denominator (e.g., 2⁄3).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 5⁄3).
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 2⁄3).
Manipulating Fractions

Here are some operations you can perform with fractions:
Adding and Subtracting Fractions

To add or subtract fractions, they must share a common denominator. Here's how to do it:
- Find the least common denominator (LCD).
- Adjust the fractions to have the same denominator.
- Add or subtract the numerators.
- Simplify if necessary.
📚 Note: When working with mixed numbers, convert them to improper fractions before manipulating, and then convert back if necessary.
Multiplying Fractions
Multiplying fractions is straightforward:
- Multiply the numerators together to get the new numerator.
- Multiply the denominators together to get the new denominator.
- Simplify if possible.
Dividing Fractions

To divide by a fraction, you multiply by its reciprocal:
- Take the reciprocal of the second fraction by swapping the numerator and the denominator.
- Proceed with multiplication as described above.
- Simplify if necessary.
Converting Between Fractions and Decimals

Understanding how to convert between fractions and decimals is crucial for practical applications. Here's how:
Converting Fractions to Decimals

Convert fractions to decimals using division:
- Divide the numerator by the denominator.
- Perform the division to get the decimal equivalent.
Example: 3⁄4 = 0.75
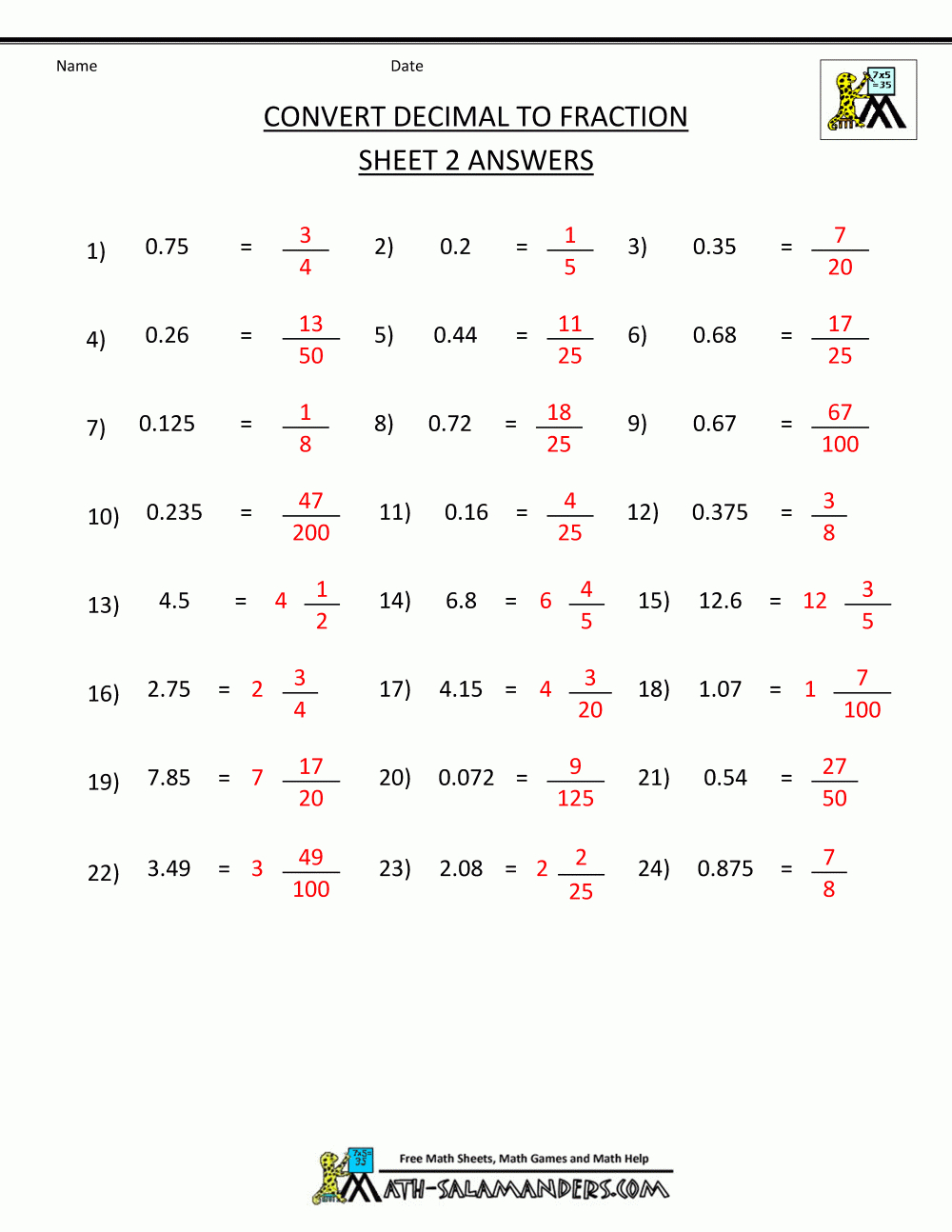
Converting Decimals to Fractions

Here's the process for turning a decimal into a fraction:
- Count the number of decimal places to determine the denominator.
- Remove the decimal point to get the numerator.
- Simplify if necessary.
Example: 0.625 = 625⁄1000 = 5⁄8
Worksheet Exercises for Practice

Enhance your skills with these exercises:
| Fraction | Add | Subtract | Multiply | Divide |
|---|---|---|---|---|
| 1⁄3 | 1⁄2 | 1⁄4 | 2⁄5 | 1⁄2 |
| 2⁄5 | 3⁄10 | 1⁄10 | 3⁄4 | 1⁄4 |

🧮 Note: Remember to simplify your answers and check your work for accuracy.
Real-Life Applications

Fractions and decimals are not just abstract concepts; they're essential in daily life:
- Measurement: Cooking, sewing, and construction all involve precise measurements.
- Financial Literacy: Understanding interest rates, discounts, and budgeting involves decimals and fractions.
- Probability and Statistics: These areas rely heavily on understanding fractional probabilities and percentage calculations.
Applying these concepts in real life helps solidify mathematical understanding and makes the math relevant and interesting.
Recapping, fractions and decimals are integral to a wide range of mathematical concepts and practical applications. By mastering these fundamentals, students can build a robust foundation for more complex mathematical endeavors. The skills developed through practice with fractions and decimals not only improve mathematical accuracy but also enhance logical reasoning and problem-solving abilities.
How do you find a common denominator?

+
The simplest method to find a common denominator is to use the least common multiple (LCM) of the denominators of the fractions you want to add or subtract.
What are the differences between a decimal and a fraction?

+
Decimals are based on powers of ten, where the position of a digit tells its value, whereas fractions express parts of a whole in terms of a numerator (top) and a denominator (bottom).
Why do we need to convert fractions to decimals?

+
Converting fractions to decimals can simplify arithmetic operations and make comparisons easier, particularly when dealing with measurements or financial calculations.