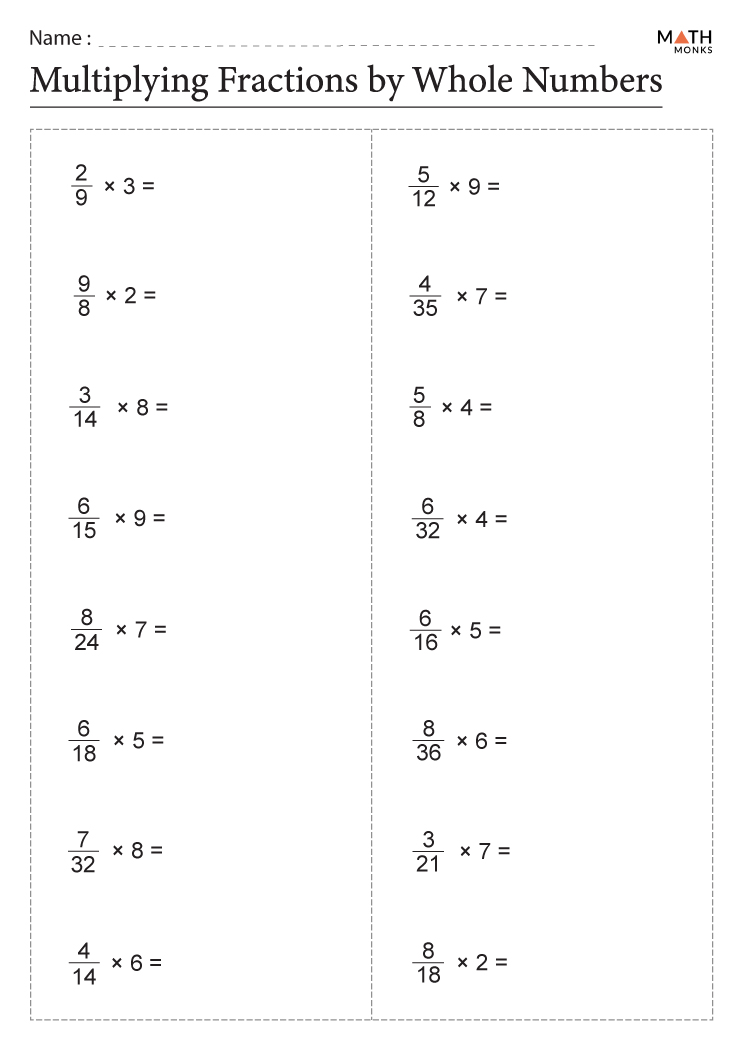
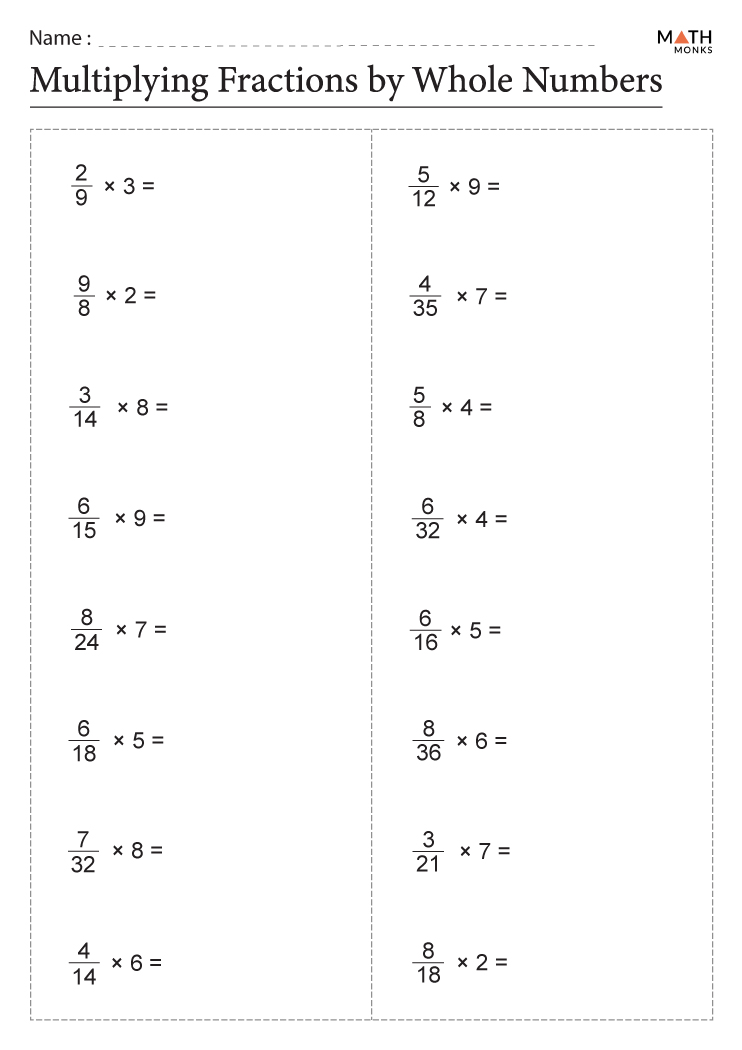
Fraction Times Whole Number Worksheet: Mastering Math with Ease

Mastering the multiplication of fractions with whole numbers is a critical mathematical skill that students often encounter in their math curriculum. It builds a foundation for more complex numerical operations and is essential for understanding various mathematical applications. This blog post will delve into the nuts and bolts of this process, guiding you through examples, providing step-by-step instructions, and sharing best practices to ensure that you can help students, or yourself, master this skill with ease.
Why Is Learning Fraction Times Whole Number Important?

- Real-World Applications: From cooking to crafting, knowing how to multiply fractions by whole numbers helps in dealing with portions, scaling recipes, and measurements.
- Foundation for Advanced Math: It’s a stepping stone to understanding algebraic expressions and operations with rational numbers.
- Critical Thinking: It promotes problem-solving and logic, encouraging a deeper understanding of numbers and their relationships.
Step-by-Step Guide to Fraction Times Whole Number Multiplication

Here are the steps you need to follow to multiply a fraction by a whole number:
- Convert the Whole Number to a Fraction: Treat the whole number as a fraction by placing it over 1. For example, 5 becomes (\frac{5}{1}).
- Multiply Numerators Together: Multiply the numerator of the fraction by the numerator of the converted whole number.
- Multiply Denominators Together: Multiply the denominator of the original fraction by the denominator of the converted whole number.
- Simplify the Fraction: If possible, simplify the resulting fraction by dividing the numerator and denominator by their greatest common divisor (GCD).
- Check for Mixed Numbers: If your result is an improper fraction, convert it to a mixed number if required.
📝 Note: Simplify your fractions at every opportunity to maintain clarity and to streamline the multiplication process.
Example Walkthrough
| Step | Operation | Result |
|---|---|---|
| 1 | (\frac{3}{4} \times 5) | (\frac{3}{4} \times \frac{5}{1}) |
| 2 | Numerators: (3 \times 5) | (15) |
| 3 | Denominators: (4 \times 1) | (4) |
| 4 | Simplify (\frac{15}{4}) | (3\frac{3}{4}) |

🧠 Note: Practicing multiple examples helps solidify the method and catch potential mistakes early.
Common Challenges and Solutions

- Not Simplifying: Many students forget to simplify fractions after multiplication, leading to unnecessarily complex results. Encourage simplification at every step.
- Confusion with Signs: If negative numbers are involved, remind students to apply the multiplication rules for signs (negative × positive = negative).
- Improper to Mixed Conversion: Some might struggle with converting improper fractions to mixed numbers. Regular practice can mitigate this.
Strategies for Teaching and Learning

- Visual Aids: Use diagrams or physical objects to demonstrate the process, making it more tangible for visual learners.
- Repeated Practice: Regular practice with different sets of numbers will enhance understanding and recall.
- Real-Life Connections: Relate problems to everyday situations, increasing the student’s engagement and understanding.
- Error Analysis: Review common mistakes and discuss ways to avoid or correct them, building a more analytical approach to learning.
🌟 Note: Relating math to real-life scenarios makes it more relatable and less abstract, which can significantly improve comprehension.
In the journey of mastering the multiplication of fractions by whole numbers, the key is to break down the process into simple, manageable steps. By following this structured approach, coupled with consistent practice and real-world examples, students can become adept at handling these operations. Remember, the goal is not just to memorize a process but to understand the underlying mathematics that make this process work. With the right strategies, tools, and mindset, every student can conquer fraction times whole number multiplication, unlocking the door to more advanced mathematical concepts.
Why do we convert whole numbers to fractions when multiplying?

+
This conversion standardizes the operation, allowing the multiplication of both numbers as if they were fractions, which simplifies the process.
What is the difference between a proper fraction and an improper fraction?

+
A proper fraction has a numerator smaller than the denominator, while an improper fraction’s numerator is greater than or equal to the denominator. Improper fractions can often be converted to mixed numbers.
How can visual aids help in understanding fraction multiplication?
+
Visual aids like diagrams or physical representations of fractions make the abstract concept more concrete, helping students visualize how fractions interact during multiplication.



