5 Tips for Mastering Fraction Multiplication and Division

In the world of mathematics, fractions are fundamental. Whether you're baking, sharing pizzas, or adjusting measurements, understanding how to multiply and divide fractions is crucial. But let's admit it, fractions can be tricky, especially when you start playing with them mathematically. Today, we're diving deep into the art of multiplying and dividing fractions with ease. Here are five strategies that will turn those intimidating operations into a walk in the park.
Understanding the Basics

What Are Fractions?
Before we dive into multiplication and division, let's have a quick refresher on what fractions are. Fractions represent parts of a whole or a ratio between two numbers. They consist of a numerator (the top number) and a denominator (the bottom number).
Representation:
- \frac{numerator}{denominator}
Fractions like \frac{1}{2}, \frac{3}{4}, or \frac{15}{20} might seem simple, but when you multiply or divide them, things can get complex. Let's clear that up with our first tip.
Tip 1: Simplify Before You Start

Multiplication and division are less daunting when you start with simplified fractions. Here's how to approach it:
- Reduce: Before multiplying or dividing, reduce each fraction to its simplest form. This simplifies calculations.
- Find common factors: Look for numbers that can divide both numerator and denominator evenly to reduce the fraction.
For example, if you have \frac{6}{10}, you can simplify it to \frac{3}{5} by dividing both numbers by 2. This makes the next steps easier to handle.
🔍 Note: Simplifying fractions beforehand can save you time and reduce the chances of errors in the final result.
Tip 2: The Cross-Multiplication Shortcut

When dividing fractions, the traditional method involves flipping the second fraction (inverting the numerator and denominator) and then multiplying. However, there's a neat trick:
- Cross-Multiply: Instead of inverting, you can cross-multiply both fractions, which often yields the answer directly.
Let's say you need to divide \frac{2}{3} by \frac{4}{5}. Instead of doing: $$\frac{2}{3} \div \frac{5}{4} = \frac{2}{3} \times \frac{4}{5} = \frac{8}{15}$$ You can cross-multiply directly: $$\frac{2}{3} \div \frac{4}{5} = \frac{(2 \times 5)}{(3 \times 4)} = \frac{10}{12} = \frac{5}{6}$$ This technique can be both time-saving and less error-prone.
Tip 3: Visualize with Diagrams
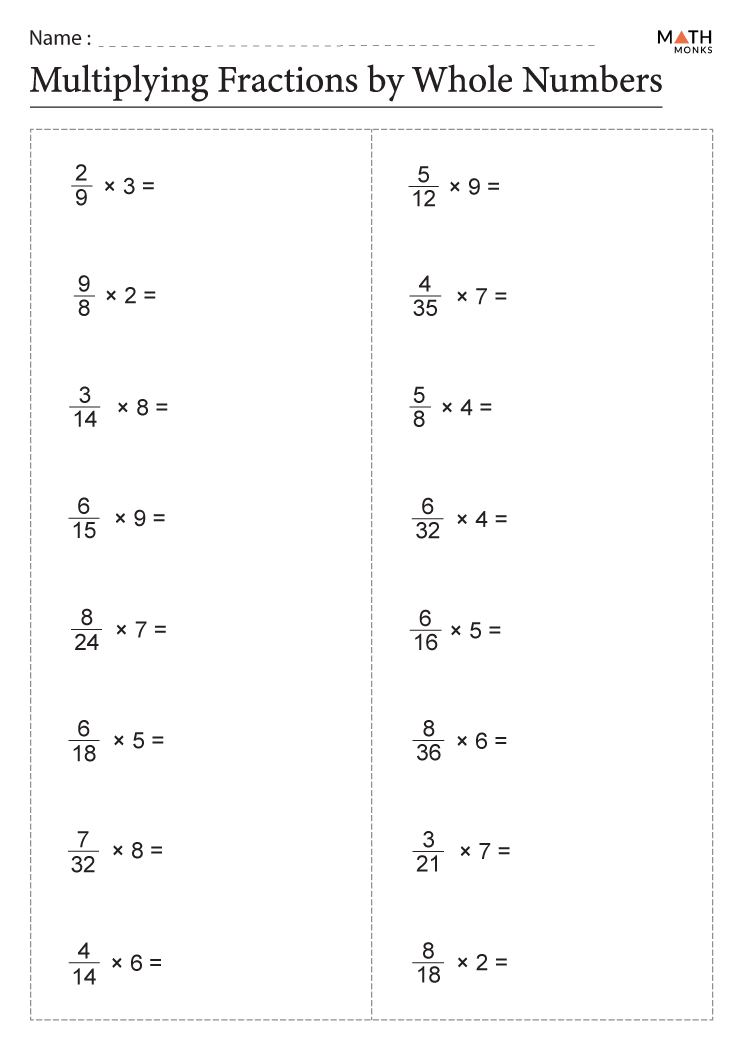
Sometimes, visual aids can bridge the gap between abstract concepts and practical understanding:
- Area Models: Use diagrams to represent multiplication or division of fractions. Visualize how these parts relate to each other.
For example, to multiply \frac{1}{4} by \frac{2}{3}, you could think of a rectangle. Divide the rectangle into 4 equal parts vertically (for \frac{1}{4}) and 3 parts horizontally (for \frac{2}{3}). The intersection of these divisions helps visualize the result.
Here's a simple representation:

The green section represents \frac{2}{12}, which simplifies to \frac{1}{6} - our desired result.
Tip 4: Using LCM for Ease

When you multiply or divide fractions, sometimes finding a common denominator can simplify things, but for division, you might need the Least Common Multiple (LCM) instead:
- LCM: Calculate the LCM of the denominators to make the division process smoother by avoiding fractions with large numbers.
Let's divide \frac{3}{7} by \frac{2}{5}:
The LCM of 7 and 5 is 35, so: $$\frac{3}{7} \div \frac{2}{5} = \frac{3}{7} \times \frac{5}{2} = \frac{15}{14} = 1\frac{1}{14}$$ Using LCM simplifies the arithmetic, especially when dealing with large or unwieldy numbers.
Tip 5: Practice with Real-Life Scenarios

Theory is great, but real-life application solidifies understanding:
- Scenarios: Apply fraction arithmetic in daily life tasks like cooking, carpentry, or even when calculating discounts on shopping.
Imagine you have \frac{3}{4} of a cake and you want to split it equally among \frac{2}{3} of your friends. How much cake does each friend get? Here, you would multiply: $$\frac{3}{4} \times \frac{3}{2} = \frac{9}{8} = 1\frac{1}{8}$$ Each friend gets 1 and \frac{1}{8} pieces of cake.
By applying these tips in real-world situations, your comfort with fraction arithmetic will grow, making you a master in no time.
Mastering fraction multiplication and division involves understanding, simplification, visualization, strategic approaches like cross-multiplication and LCM, and practical application. By incorporating these tips into your learning process, you'll not only improve your math skills but also find joy in solving what once seemed like complex problems. The key is practice, patience, and understanding the underlying concepts that make these operations manageable. So, next time you encounter fractions, remember these tips, and tackle them with confidence.
How do I know if a fraction can be simplified?
+
Check if both the numerator and the denominator share common factors greater than 1. If they do, divide both by the greatest common factor to simplify the fraction.
Is there a shortcut to find the Least Common Multiple (LCM) for denominators?
+
Yes, you can list the multiples of each denominator until you find the smallest number that appears in both lists. Alternatively, use the prime factorization method for more complex cases.
What’s the importance of visualization in fraction arithmetic?

+
Visual aids help create a concrete understanding of abstract concepts, making it easier to grasp how fractions interact with each other through multiplication and division.
Why should I use real-life scenarios when learning fraction operations?

+
Real-life scenarios provide context, which helps in understanding the application of math. It also makes learning more engaging and less theoretical, enhancing retention and problem-solving skills.
Can I always use cross-multiplication for fraction division?

+
Yes, cross-multiplication is a valid shortcut for dividing fractions, provided you remember to divide the resulting product by the product of the denominators.