Fraction, Decimal, and Percent Conversion Worksheet Fun
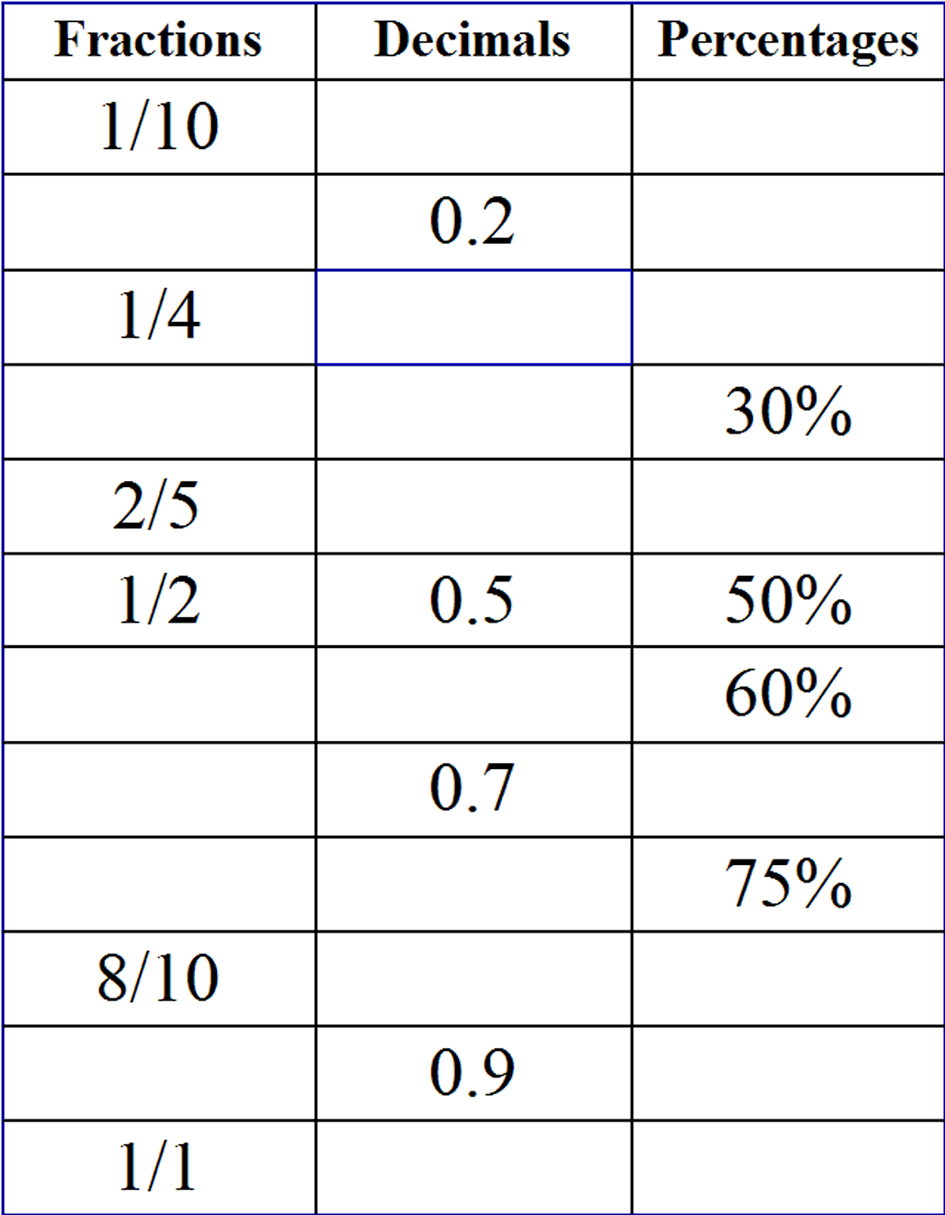
Converting between fractions, decimals, and percentages is a fundamental mathematical skill that not only helps in solving academic problems but also aids in everyday tasks like cooking, financial calculations, and more. This guide will explore different methods to convert these numerical expressions easily, offering worksheets and tips to make the learning process fun and effective.
Understanding the Basics
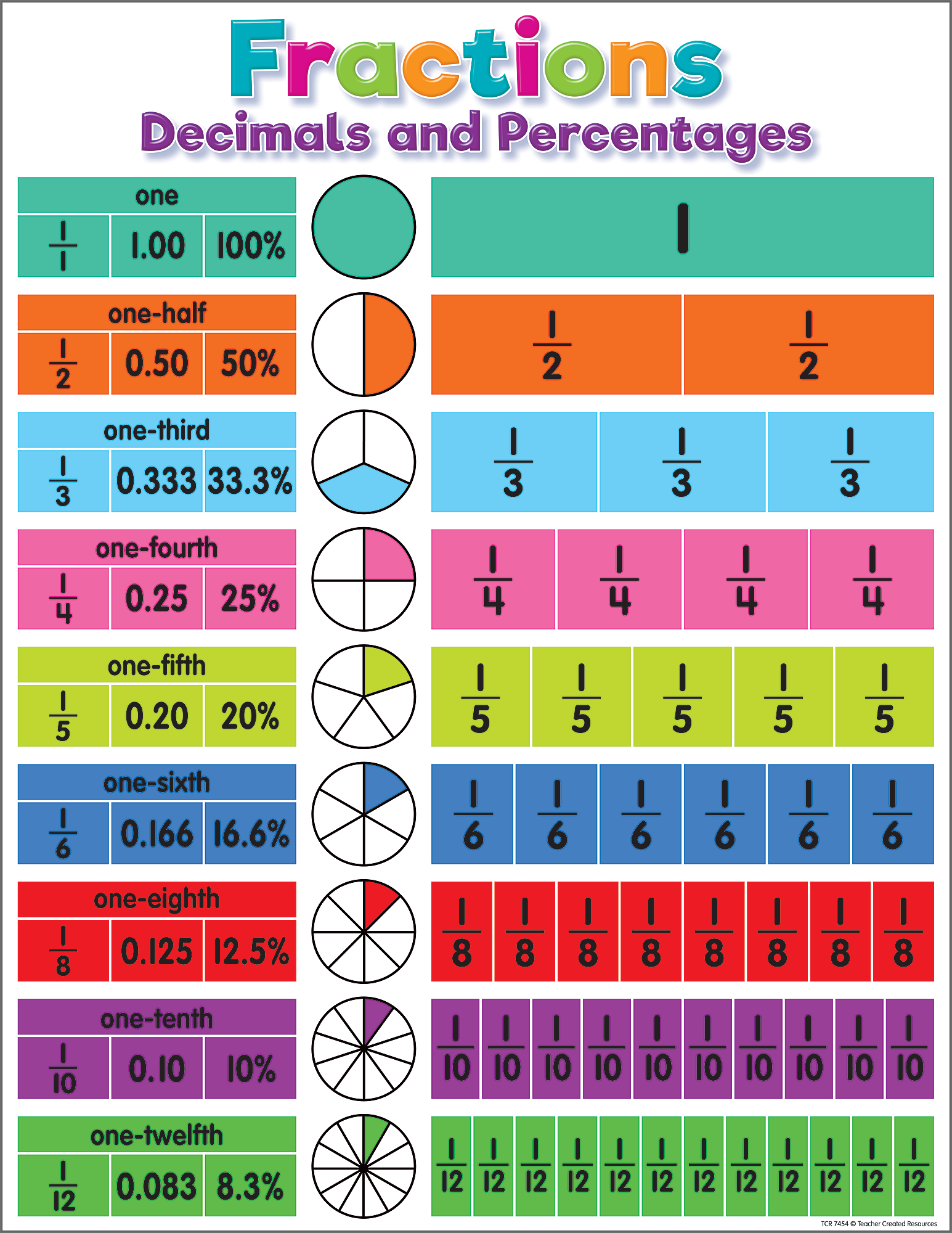
Before diving into conversions, let’s understand what each form represents:
- Fraction: Represents a part of a whole or a number divided by another. For example, 1⁄4 means one part out of four equal parts.
- Decimal: A number expressed with a decimal point, such as 0.25, where the digits after the point represent tenths, hundredths, etc.
- Percent: Indicates parts per hundred. A percent like 25% means 25 out of 100 or 25⁄100.
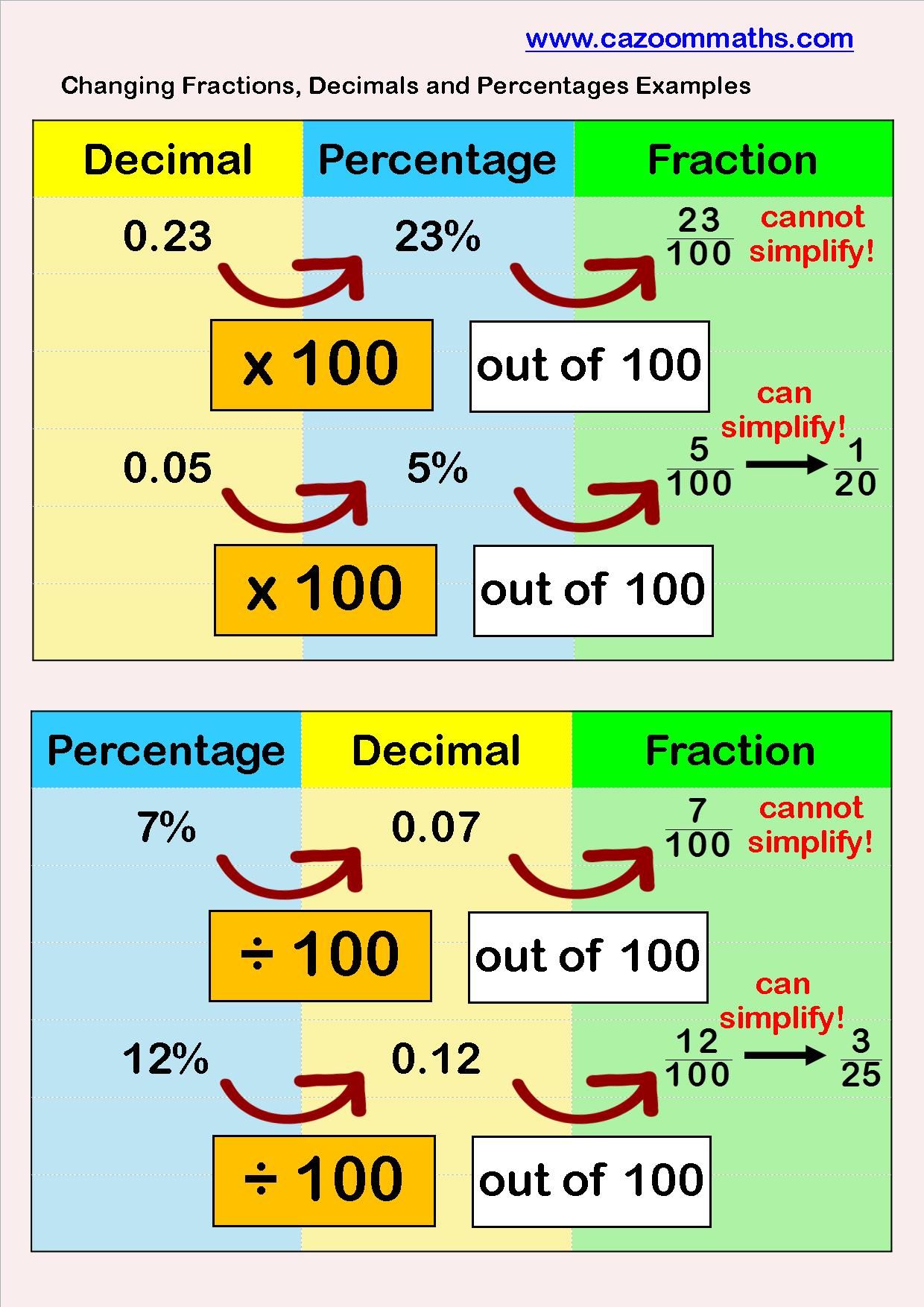
Converting Fractions to Decimals

To convert a fraction to a decimal:
- Divide the numerator (the top number) by the denominator (the bottom number).
- The result is the decimal equivalent.
🔍 Note: Long division might be needed for some fractions leading to repeating decimals.
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 1/4 | 0.25 |
| 3/4 | 0.75 |

From Fractions to Percentages

The method to convert a fraction to a percentage is:
- Convert the fraction to a decimal using the above method.
- Multiply the decimal by 100 to get the percentage.
| Fraction | Decimal | Percentage |
|---|---|---|
| 1/2 | 0.5 | 50% |
| 1/4 | 0.25 | 25% |
| 3/4 | 0.75 | 75% |
Converting Decimals to Fractions
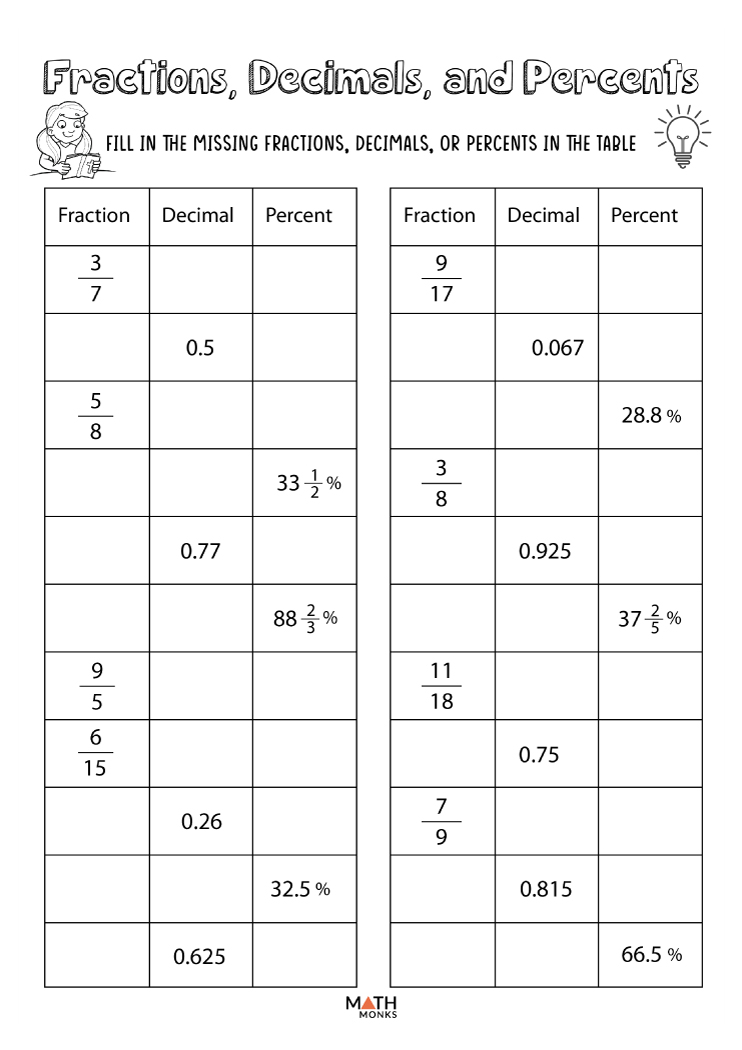
Here’s how to convert a decimal into a fraction:
- Write down the decimal divided by 1.
- Multiply both numerator and denominator by 10 for each decimal place.
- Simplify the fraction by finding the greatest common divisor (GCD).
| Decimal | Fraction |
|---|---|
| 0.2 | 1/5 |
| 0.3 | 3/10 |
| 0.75 | 3/4 |
From Decimals to Percentages

The easiest way to convert a decimal to a percentage:
- Multiply the decimal by 100.
🔎 Note: Ensure your calculator is in standard mode to avoid unnecessary scientific notation conversions.
Converting Percentages to Fractions

Here’s how to change a percentage into a fraction:
- Divide the percentage by 100 to get the decimal form.
- Convert the decimal to a fraction using the method described above.
| Percentage | Fraction |
|---|---|
| 25% | 1/4 |
| 50% | 1/2 |
| 75% | 3/4 |
Worksheet Fun: Interactive Conversions
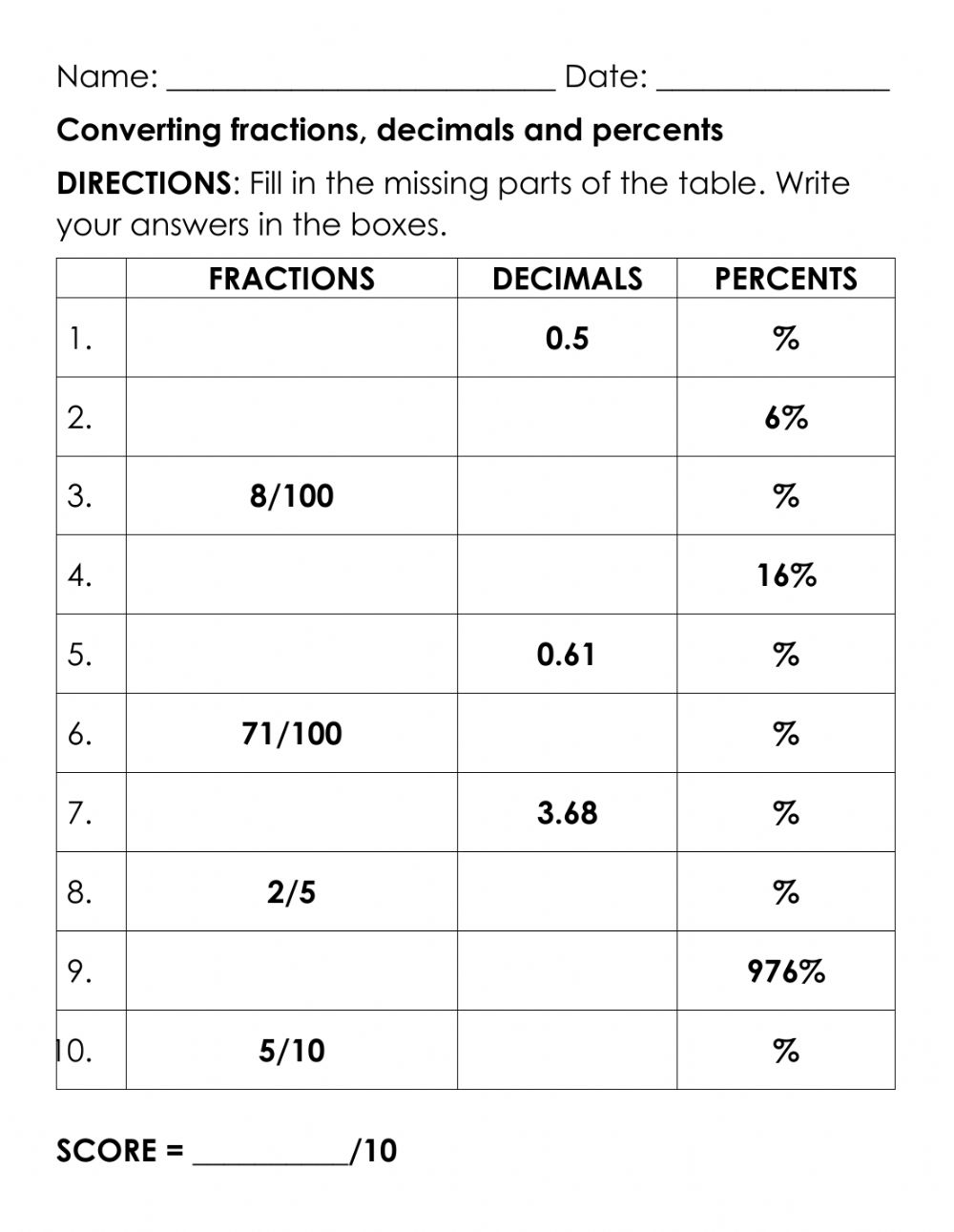
Converting numbers between different forms can be made fun with worksheets:
- Create a bingo game where players match numbers in different forms.
- Make puzzles where pieces are fractions, decimals, and percentages that need to be matched.
- Design a treasure hunt where clues are given in one form, and the answer must be found in another.
📋 Note: These activities enhance both understanding and retention of the conversion methods.
Final Takeaway
Understanding the conversion between fractions, decimals, and percentages is crucial for anyone dealing with mathematical or financial tasks. This guide has outlined the straightforward techniques for these conversions, and by practicing with interactive worksheets and games, learners can solidify their skills in an engaging manner. Here are some key points to remember:
- Each numerical form has its unique representation and application.
- The process of conversion can be systematically approached through division, multiplication, or simplification.
- Making learning fun through interactive methods can significantly boost understanding and retention.
Why is it important to know how to convert between fractions, decimals, and percentages?

+
Converting between these forms allows for easier comparisons, understanding ratios, and applying mathematical concepts in real-world scenarios.
Can a fraction always be accurately represented as a decimal or percentage?

+
Not always. Some fractions result in repeating decimals which cannot be exactly represented as a finite decimal or percentage.
How can I simplify a fraction?

+
To simplify a fraction, divide both the numerator and the denominator by their greatest common divisor (GCD).
Are there any tools or apps for practicing these conversions?

+
Yes, there are numerous math apps and online tools available that offer interactive exercises and quizzes for conversion practice.
What’s the best way to remember these conversion methods?
+
Regular practice, understanding the relationship between the forms, and using memory aids or mnemonics can help in remembering conversion methods.