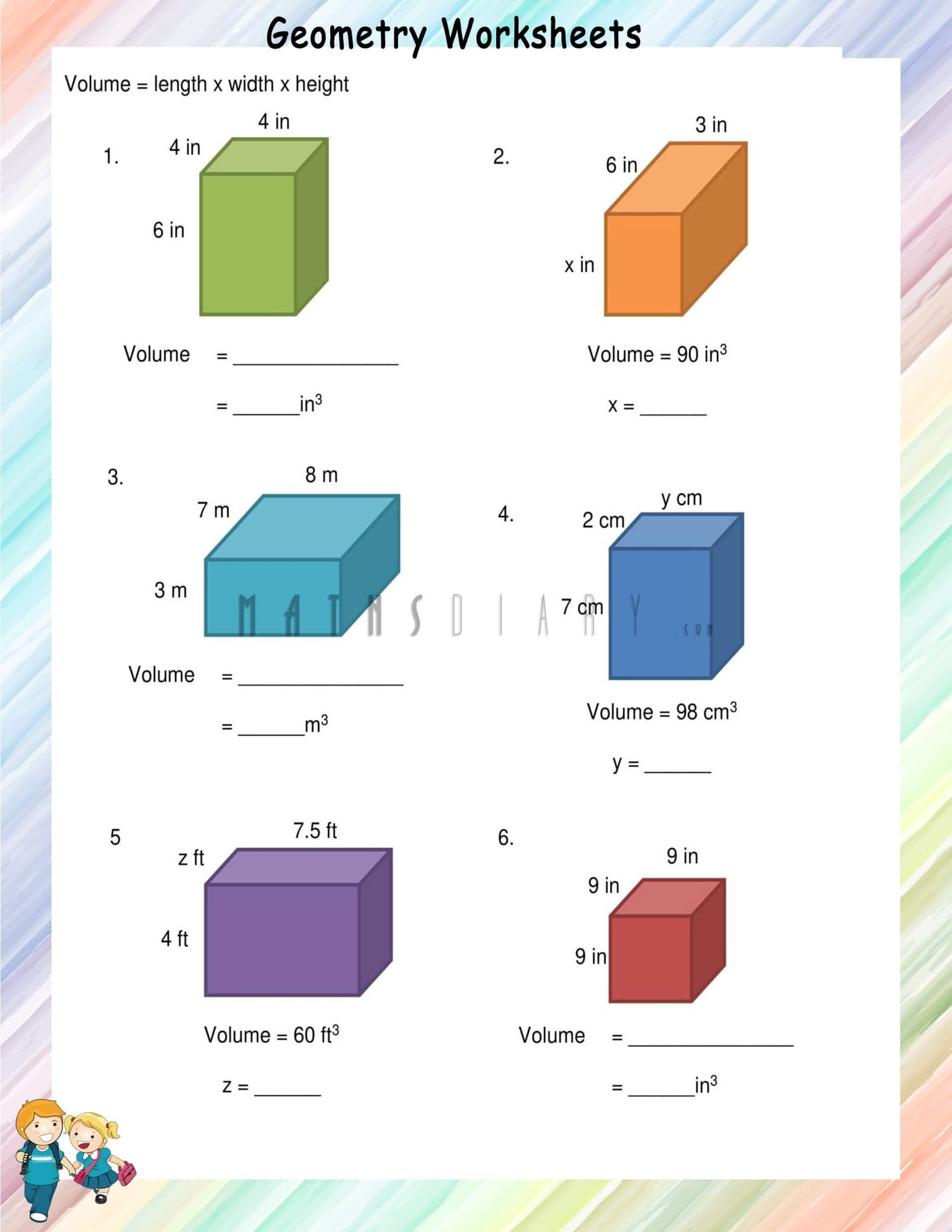
Discover Volume of Rectangular Prisms: Engaging Worksheet

Volume is a fundamental concept in geometry, particularly when dealing with three-dimensional shapes. Among these shapes, the rectangular prism, also known as a cuboid, is one of the most commonly encountered. Understanding how to calculate its volume not only deepens our knowledge of geometry but also equips us with practical skills useful in everyday scenarios, from architecture to simple home improvement projects. In this article, we'll delve into an engaging approach to teach and understand the volume of rectangular prisms through a worksheet tailored to enhance both learning and application.
Why Volume Calculation Matters
Understanding volume is not just an academic exercise; it's a practical skill:
- Space Planning: Architects and builders need to calculate how much material or space is required for a project.
- Volume in Cooking: Chefs measure out the right amount of ingredients, understanding volume in terms of liters, cups, or other measurements.
- Storage: Knowing how to calculate volume can help in deciding how much storage space you need or how to best pack items.
Calculating Volume of Rectangular Prisms
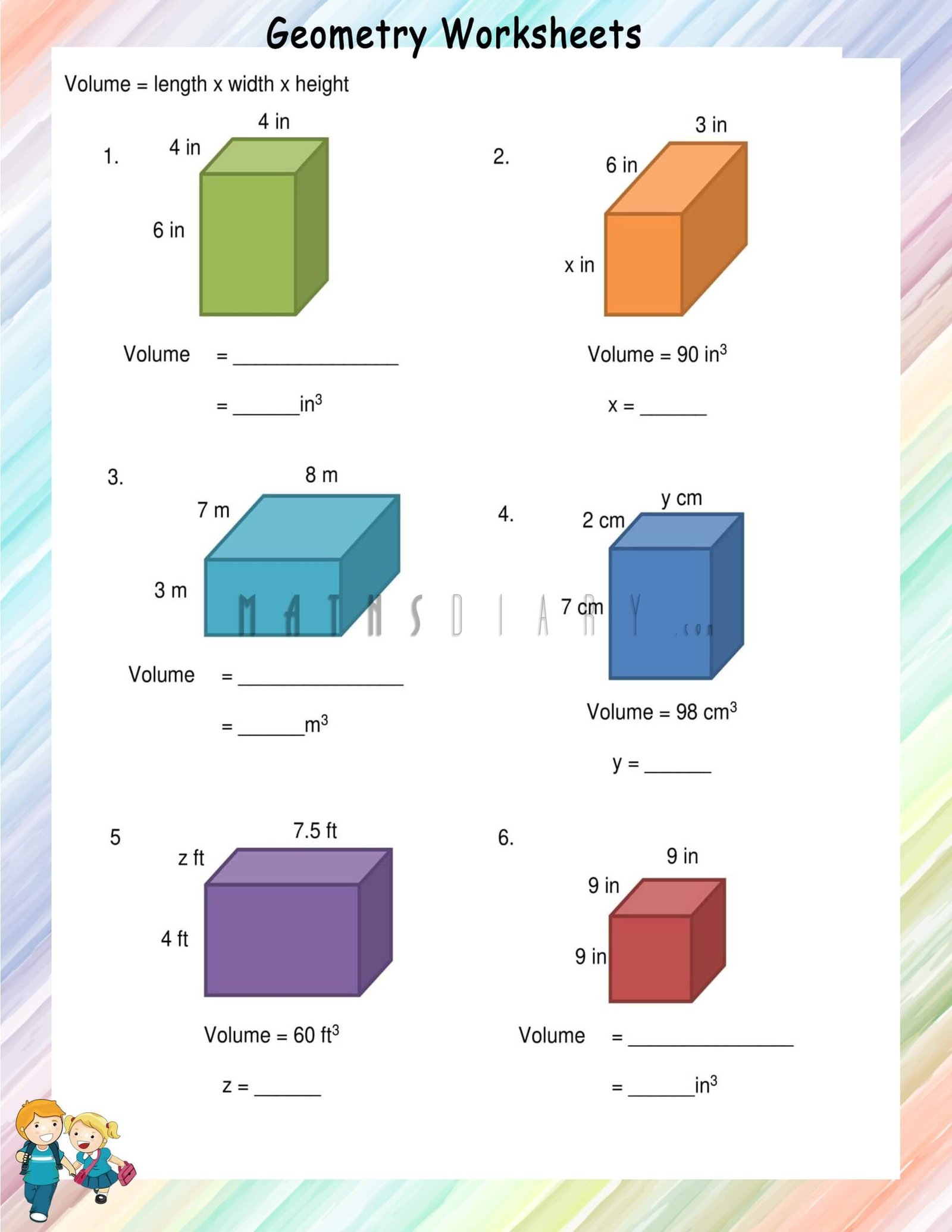
The formula for calculating the volume (V) of a rectangular prism is straightforward:
V = l * w * h
where l is the length, w is the width, and h is the height of the prism. This simple multiplication gives us the volume in cubic units.

Engaging Worksheet for Volume of Rectangular Prisms

| Problem | Dimensions | Volume |
|---|---|---|
| 1. A Box | l=3 units, w=4 units, h=2 units | |
| 2. A Room | l=5 units, w=7 units, h=8 units | |
| 3. A Tank | l=12 units, w=5 units, h=8 units | |
| 4. A Shoebox | l=30 cm, w=15 cm, h=10 cm | |
| 5. A Gift Box | l=12 inches, w=10 inches, h=6 inches |

Solutions

- 1. A Box: V = 3 * 4 * 2 = 24 cubic units
- 2. A Room: V = 5 * 7 * 8 = 280 cubic units
- 3. A Tank: V = 12 * 5 * 8 = 480 cubic units
- 4. A Shoebox: V = 30 * 15 * 10 = 4500 cubic cm or 4.5 liters
- 5. A Gift Box: V = 12 * 10 * 6 = 720 cubic inches
By engaging with these problems, learners can actively apply the formula, understanding not only how to calculate but also the practical implications of volume in different real-world contexts.
💡 Note: When calculating the volume, ensure that all measurements are in the same units. For example, if length is given in meters, width and height must also be in meters.
Visualizing Volume

Understanding volume visually can enhance comprehension:
- Using Scale: Creating or visualizing a model of the prism with given dimensions helps in understanding how volume expands.
- Volume Visualization Apps: There are various apps that can simulate the addition or subtraction of cubic units, aiding in real-time visual learning.
- 3D Printing: Printing out scaled-down models of rectangular prisms can provide a tactile learning experience.
Advanced Volume Problems

Once the basic concept is mastered, learners can tackle more complex scenarios:
- Dividing Volumes: How to divide a volume into equal parts or by specific ratios.
- Composite Volumes: Calculating the volume of shapes made by combining several rectangular prisms.
- Estimation: Estimating volume when exact measurements are not available, fostering critical thinking.
By exploring these advanced concepts, students gain a broader understanding of geometry and its practical applications.
💡 Note: While solving volume problems, remember that changing one dimension can significantly affect the volume. Doubling the height of a rectangular prism, for example, doubles the volume.
As we've journeyed through the volume of rectangular prisms, we've not only learned a formula but also developed a deeper appreciation for how geometry applies to the world around us. From packing a suitcase to designing a skyscraper, the understanding of volume allows us to estimate, plan, and innovate in both small and grand scales. This foundational knowledge empowers learners to think spatially, critically assess problems, and apply mathematical concepts in everyday life or professional contexts.
Why is understanding volume important in real life?

+
Understanding volume is crucial for tasks like planning storage, designing living spaces, or even in everyday activities like cooking and gardening, where knowing how much space or material is needed can be vital.
Can the volume formula be used for shapes other than rectangular prisms?

+
While the formula l * w * h is specific to rectangular prisms, similar principles apply to other shapes with adaptations. For example, for a cylinder, the formula changes to πr²h.
How does unit conversion affect volume calculations?

+
Converting between units changes the volume proportionally. For instance, converting from centimeters to meters will multiply or divide the volume by 1,000,000 because one meter³ equals 1,000,000 cm³.