5 Easy Steps to Find Slope on Worksheets

Learning how to find the slope on worksheets can be a game-changer for mastering algebra, geometry, and other math subjects. Slope, often referred to as the gradient or incline, is not just a measure of how steep a line is; it's the heart of linear equations and graphical analysis. Whether you're a student struggling to understand the concept or a tutor aiming to explain it succinctly, this guide will walk you through 5 easy steps to master the calculation and interpretation of slopes on any worksheet or graph.
Finding Slope Defined
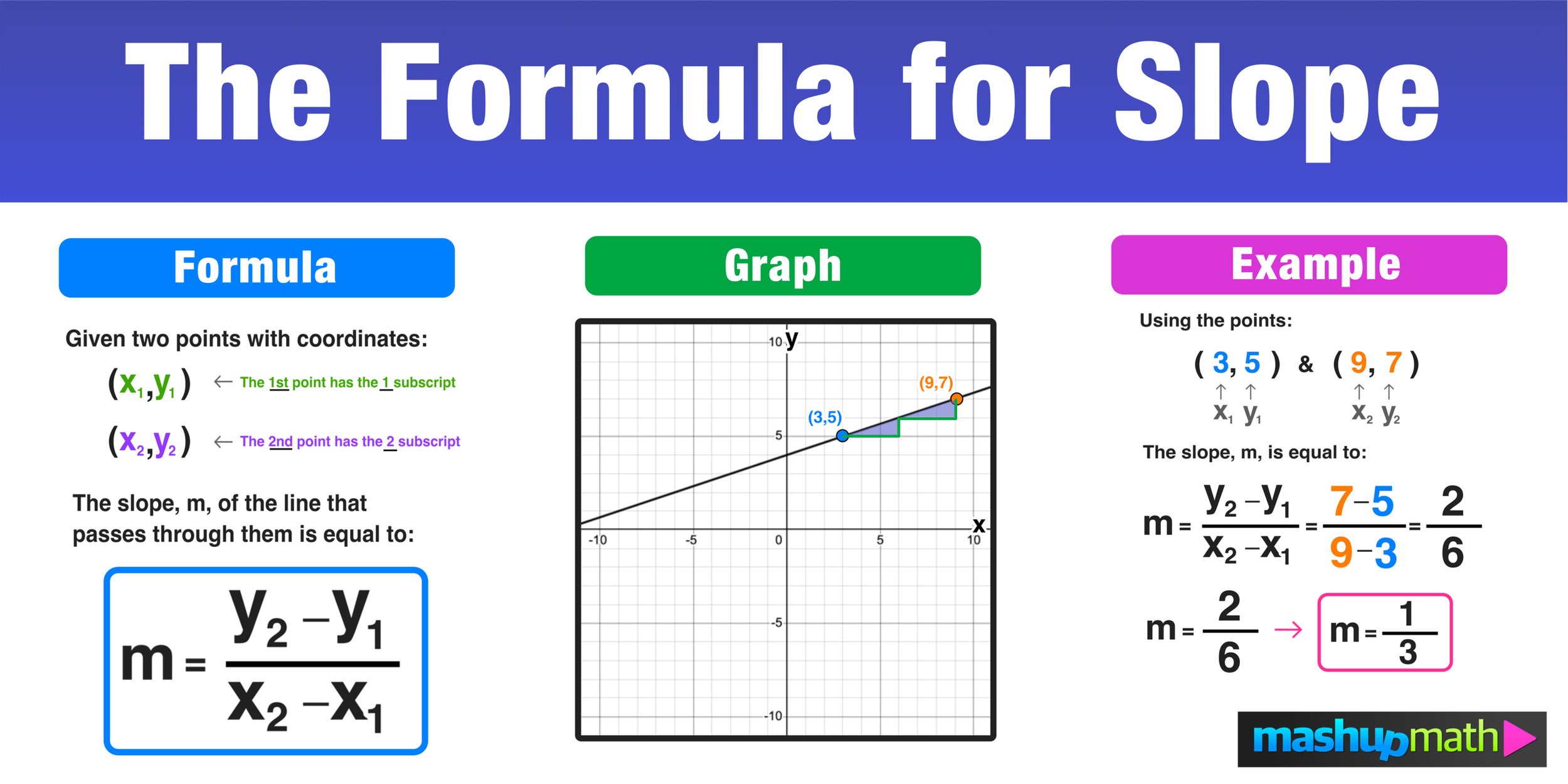
Before diving into the steps, let’s quickly define what slope means. Slope in mathematics is the ratio of the vertical change (the rise) to the horizontal change (the run) between any two points on a line. It’s usually symbolized by the letter m and can be calculated using the formula:
m = (y2 - y1) / (x2 - x1)
Step 1: Identify the Points on Your Worksheet

Your first task is to identify two distinct points on the line you’re analyzing. These points could be given directly, or you might need to plot the line from an equation to find them. Here are some pointers to keep in mind:
- Look for coordinates labeled on the worksheet or graph.
- If no points are given, use the x and y-intercepts or solve for coordinates from the equation.
🔍 Note: Points should be chosen such that the line doesn’t cross them exactly at the y or x-axis unless you’re specifically looking for slopes of lines passing through the origin or with zero run.
Step 2: Determine the Change in Y (Rise)

With your points identified, calculate the vertical change or ‘rise’ between the two. Here’s how you do it:
- Subtract the y-coordinate of the second point from the y-coordinate of the first point.
- Note that the order of subtraction matters; typically, you’ll subtract from top to bottom if viewing the graph.
📈 Note: The change in Y can be positive, negative, or zero, which indicates the direction and steepness of the line.
Step 3: Calculate the Change in X (Run)

Now, find the horizontal change or ‘run’ by performing a similar subtraction:
- Subtract the x-coordinate of the second point from the x-coordinate of the first point.
- Again, consistency in order is key.
📏 Note: The run will dictate how wide the line travels horizontally; a large run means a less steep slope.
Step 4: Apply the Slope Formula
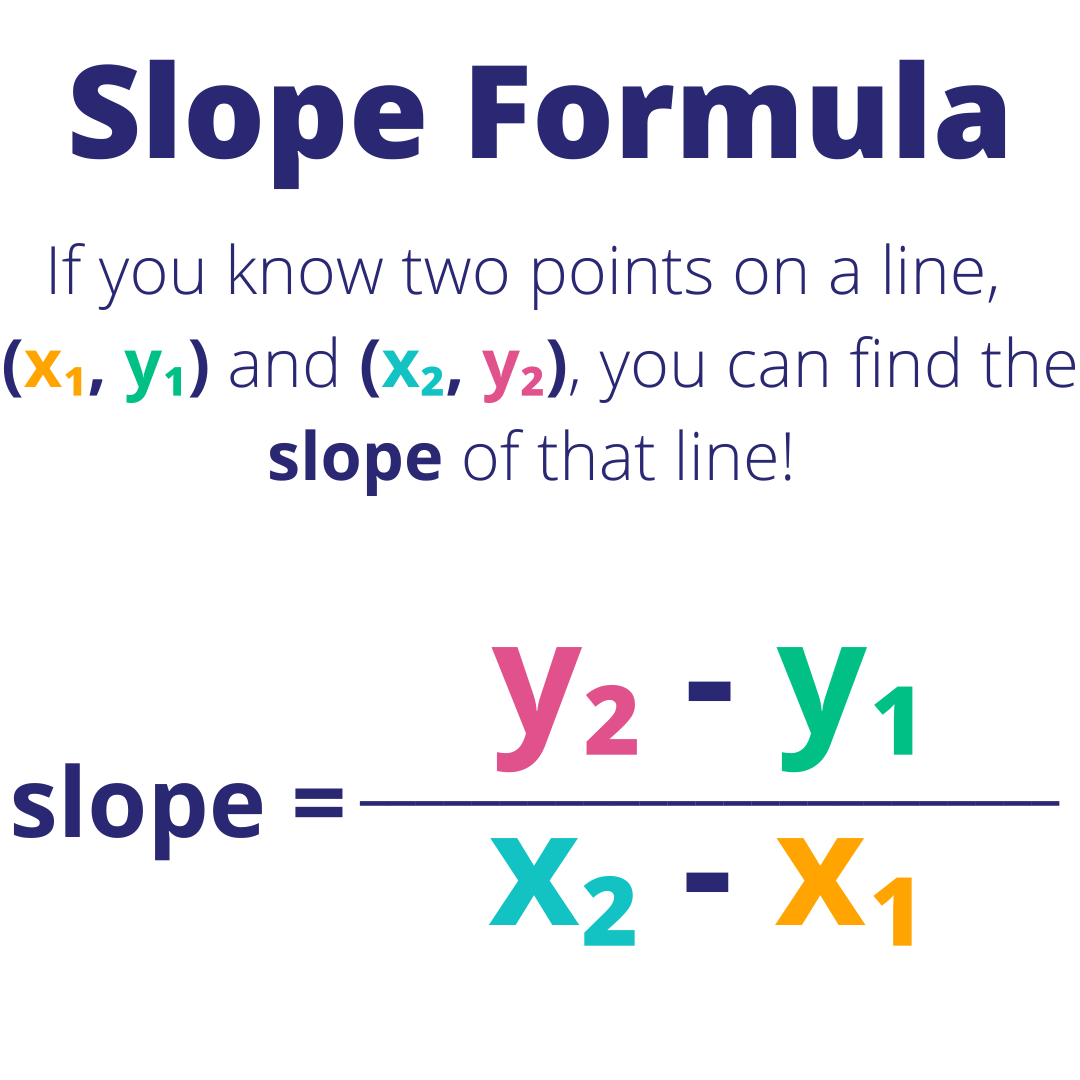
With your rise and run in hand, plug them into the slope formula:
- m = (y2 - y1) / (x2 - x1).
Let’s break it down with an example:
| Point 1 | Point 2 | Rise (y2-y1) | Run (x2-x1) | Slope (m) |
|---|---|---|---|---|
| (2, 3) | (5, 7) | 4 | 3 | 4⁄3 |

Step 5: Interpret the Slope

Once you’ve computed the slope, what does it mean?
- Positive slope: The line is increasing from left to right.
- Negative slope: The line is decreasing from left to right.
- Zero slope: The line is horizontal.
- Undefined slope: The line is vertical.
Slope has practical applications in fields like physics, engineering, economics, and beyond, making it crucial to understand its implications:
- It indicates how steep or gentle a hill or incline is.
- In finance, it can show how quickly assets are depreciating or appreciating.
💡 Note: Always remember that the slope gives you the rate of change. If the slope is constant, the rate of change is uniform across the line.
The process of finding the slope on worksheets is not merely an academic exercise but a skill that sharpens your analytical thinking. Whether you're analyzing stock trends, engineering structures, or predicting future population growth, understanding how to calculate and interpret slopes is invaluable. By following these steps, you can confidently tackle any worksheet or real-world problem that involves slopes, making the math behind them less daunting and more insightful.
What does it mean when the slope is zero?
+
A zero slope means the line is perfectly horizontal, indicating no change in the y-coordinate as the x-coordinate changes.
Can slope be negative?
+
Yes, a negative slope indicates that as x increases, y decreases, and the line slopes downward from left to right.
How can I find the slope of a line on a graph?

+
To find the slope on a graph, choose two points on the line, calculate the rise over the run between them, and apply the slope formula: m = (y2 - y1) / (x2 - x1).
What does an undefined slope mean?

+
An undefined slope refers to a vertical line where the x-coordinates do not change, making the denominator of the slope formula (run) zero, resulting in an undefined division by zero.
Why is finding slope important?

+
Understanding slope is crucial for interpreting and predicting behavior in various contexts like physics, engineering, economics, and everyday decision making where change and rate of change are involved.