5 Simple Steps for Finding Slope: 8th Grade Guide
In middle school, one of the key concepts students are introduced to in algebra is finding the slope of a line. This guide will take you through the process in a clear and understandable way, making it easier for 8th graders to grasp this fundamental idea. Let's dive into the 5 simple steps for finding slope, ensuring you'll master this topic with ease.
What is Slope?

Slope is essentially the steepness of a line in a graph. It represents how much the line rises or falls as you move horizontally across the graph. In simple terms, if you imagine walking up a hill, the slope is how steep that hill is.
Formula for Slope
The mathematical formula for calculating the slope between two points ((x_1, y_1)) and ((x_2, y_2)) is:
[ \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1} ]
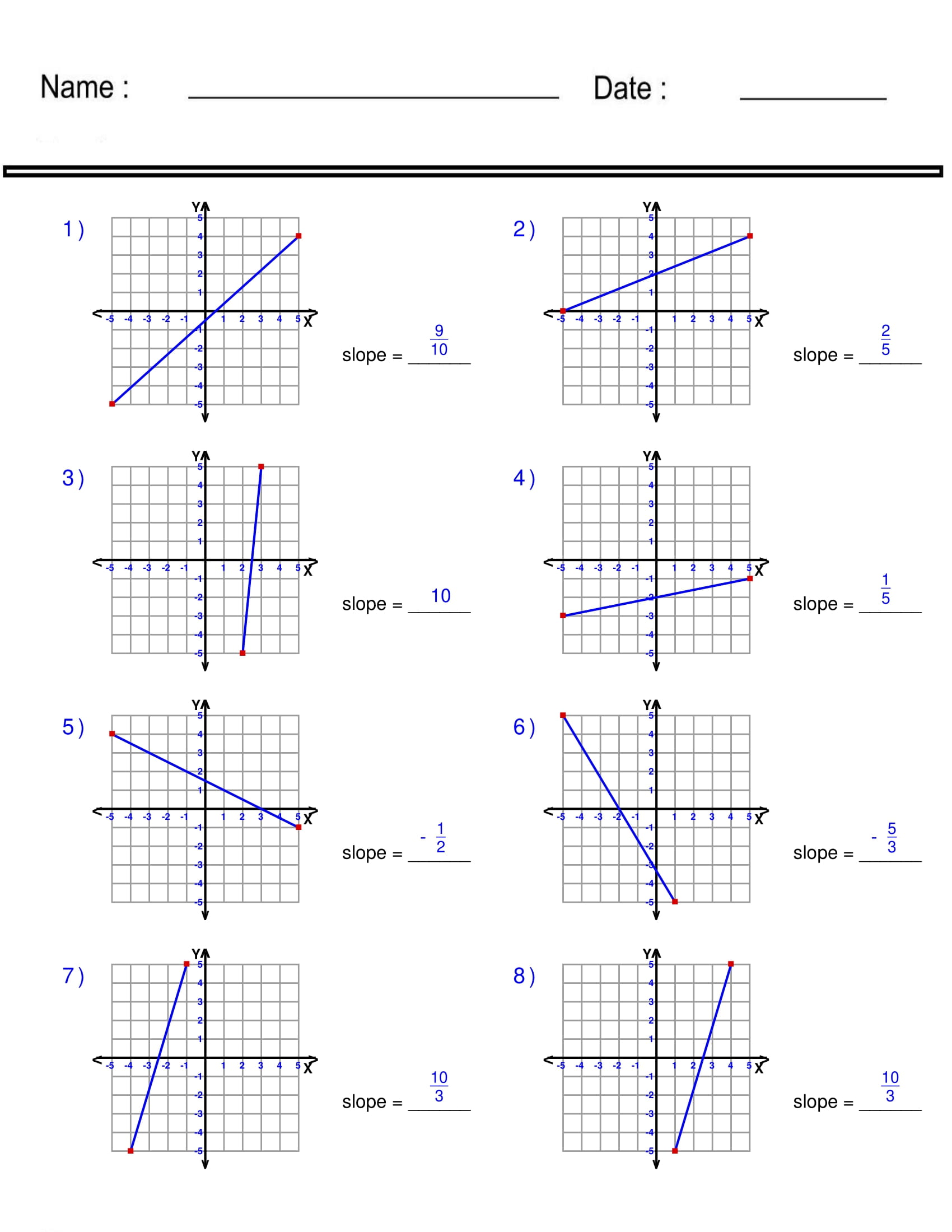
Step 1: Identify Two Points
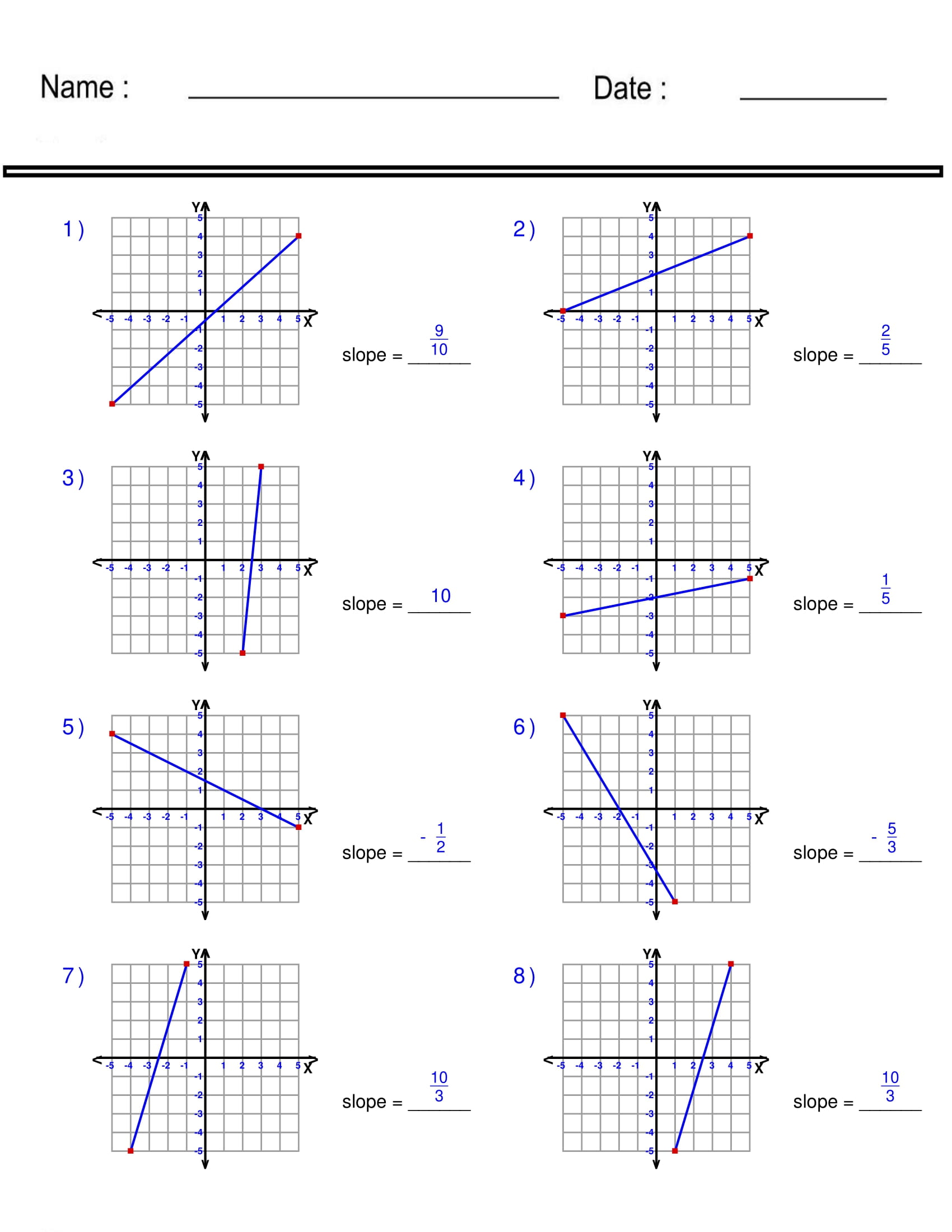
The first step to find the slope is to identify two points on the line. These points can come from your data set or be given as coordinates in a problem:
- Label them as ((x_1, y_1)) and ((x_2, y_2)).
- It doesn’t matter which point you label as 1 or 2; just keep it consistent when plugging into the formula.
Step 2: Find the Difference in Y-coordinates

Now, we focus on the vertical distance between these points. To do this, subtract the y-coordinate of the first point from the y-coordinate of the second point:
- Calculate (y_2 - y_1).
Step 3: Find the Difference in X-coordinates

Next, we calculate the horizontal distance. Subtract the x-coordinate of the first point from the x-coordinate of the second:
- Calculate (x_2 - x_1).
Step 4: Divide the Rise by the Run

With the rise and run calculated, apply the slope formula:
- Divide the difference in y-coordinates by the difference in x-coordinates: (\frac{y_2 - y_1}{x_2 - x_1}).
- The result is the slope of the line connecting the two points.
Step 5: Interpreting the Slope

Understanding what the slope tells you is crucial:
- A positive slope indicates that the line is rising from left to right.
- A negative slope means the line is falling from left to right.
- If the slope is zero, the line is horizontal, not changing vertically.
- An undefined slope, where the run is zero, indicates a vertical line.
Notes on Slope Interpretation

The slope also tells us about the steepness:
- Steeper lines have a greater numerical slope.
- Gentler lines have a smaller numerical slope.
💡 Note: Always double-check your work. Mistakes in reading coordinates or miscalculations can lead to the wrong slope.
After understanding these steps, you should be well-equipped to handle any slope-finding task in your 8th-grade math class. Slope is a critical concept as you move into more advanced math, including topics like the equation of lines, linear functions, and solving systems of equations. Remember, practicing with different pairs of coordinates will help solidify your understanding and improve your skills in quickly determining the slope.
Why is slope important in real life?

+
Slope is essential in many practical scenarios such as determining the incline of ramps for wheelchair accessibility, calculating the angle of a roof for construction, predicting growth rates in investments, and analyzing trends in data sets like weather patterns or stock market performance.
Can slope be negative?
+
Yes, a negative slope indicates that the line is falling from left to right, meaning the y-value decreases as the x-value increases.
What does an undefined slope mean?

+
An undefined slope occurs when the run (difference in x-coordinates) is zero, creating a vertical line. This means the line is completely vertical, and there is no horizontal movement.