5 Ways to Master Slope Calculation

Understanding slope calculation is essential for various fields including mathematics, engineering, construction, and even in everyday tasks like assessing the angle of a ramp or a staircase. Whether you are a student grappling with geometry, or a professional designing landscapes, mastering the art of calculating slopes can streamline your projects and enhance your efficiency. Here are five methods to master slope calculation:
1. The Slope Formula: Rise Over Run
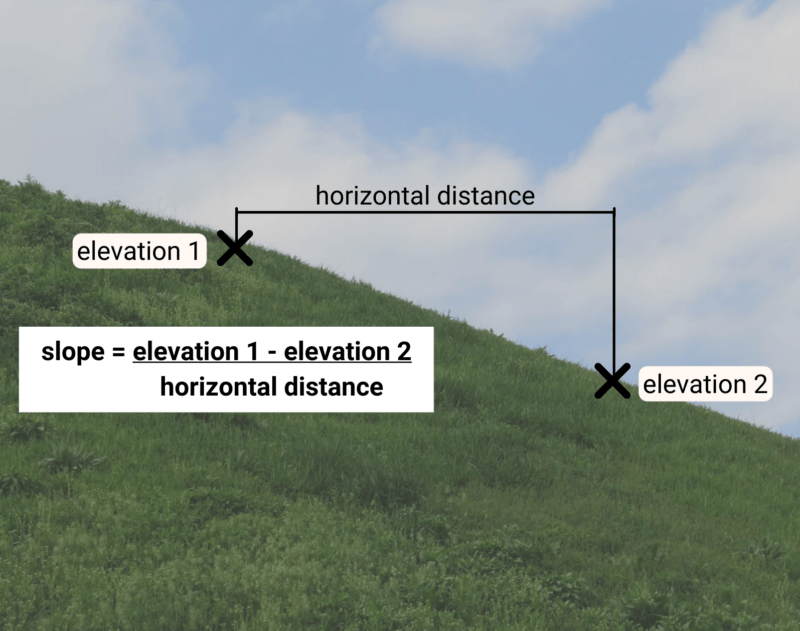
The most common and straightforward method to calculate a slope is by using the rise over run formula. Here’s how you do it:
- Identify the Vertical Change (Rise): This is the difference between the y-coordinates of two points on your line or graph.
- Identify the Horizontal Change (Run): This is the difference between the x-coordinates of the same two points.
- Calculate the slope with the formula: [ \text{Slope} = \frac{\text{Rise}}{\text{Run}} = \frac{y_2 - y_1}{x_2 - x_1} ]
⚠️ Note: Always ensure the order of subtraction remains consistent to avoid negative slope errors.
2. Using Trigonometry: Angle of Incline

For those familiar with trigonometry, calculating slope can be done through the tangent function, which relates the angle of incline to the slope:
- Measure or know the angle of incline, say (θ).
- The slope (m) can then be calculated as: [ m = \tan(θ) ]
3. Graphing for Visualization

Visualizing the slope through graphing can provide a deeper understanding:
- Plot two points on a graph.
- Draw a line through these points.
- Use the rise over run method visually to ascertain the slope.
| Point 1 | Point 2 | Rise (y_2 - y_1) | Run (x_2 - x_1) | Slope (Rise/Run) |
|---|---|---|---|---|
| (2, 3) | (6, 7) | 4 | 4 | 1 |
| (-1, 2) | (3, -2) | -4 | 4 | -1 |

📈 Note: Graphing is particularly useful for understanding the steepness of the line visually.
4. Slope of Lines in Coordinate Geometry

Understanding the types of lines in coordinate geometry can aid in slope calculation:
- Horizontal Lines have a slope of 0 because there is no vertical change.
- Vertical Lines have undefined slopes because the horizontal change is 0, leading to division by zero.
- Positive Slope indicates an upward slant from left to right.
- Negative Slope shows a downward slant from left to right.
The mathematical representation for these lines is as follows:
- (y = b) for horizontal lines where (b) is the y-intercept.
- (x = a) for vertical lines where (a) is the x-intercept.
5. Utilizing Software Tools

Modern technology offers tools that can simplify slope calculation:
- Spreadsheet Software: Use functions like SLOPE in Excel to calculate slopes with pre-filled data.
- GIS Software: For professionals dealing with topography or land design, tools like ArcGIS provide functionalities to calculate slopes across digital elevation models.
- Online Calculators: Numerous websites offer slope calculators where you can input point coordinates and get instant results.
By integrating these five methods into your understanding of slope calculation, you're not only expanding your toolkit but also enhancing your problem-solving capabilities across different disciplines. Slope calculation, though seemingly simple, is integral in various real-world applications from engineering projects to everyday life tasks. Each method provides a different perspective and approach, ensuring that you can tackle slope-related challenges with confidence and versatility.
What is the difference between slope and incline?

+
In geometry and physics, slope refers to the steepness or gradient of a line, while incline often refers to an actual angle or the degree of slanting surface in real-life applications.
Can the slope of a line be negative?

+
Yes, if a line slants downward from left to right, its slope is negative.
How does slope affect construction and design?
+
Slope calculations are crucial in construction for ensuring proper drainage, stability of structures, and safety of ramps or stairs. They influence the design to prevent water pooling, ensure structural integrity, and comply with accessibility standards.
Why does the slope of a vertical line undefined?
+
A vertical line has an undefined slope because there’s no horizontal movement (run), which means division by zero when calculating the slope, leading to an undefined value.
What tools can help with slope calculations in everyday life?

+
Smartphones often have built-in apps for leveling or simple slope calculators. Digital levels, inclinometers, or even apps like Clinometer can be very useful for quick slope checks.