Slope from Equation: Quick & Easy Worksheet Guide

Understanding how to extract the slope from a linear equation is a fundamental skill in algebra and beyond, crucial for analyzing trends, predictions, and real-world applications. This guide offers a straightforward worksheet to help you quickly master this technique. Whether you're a student tackling algebra for the first time or an educator seeking to explain this concept effectively, this guide will provide the clarity and practice you need.
The Basics of Slope

Before diving into specific methods, let’s review what slope actually is:
- Slope represents the steepness or incline of a line.
- In the equation (y = mx + b), m stands for the slope, determining how much y increases for every unit increase in x.
To find the slope from an equation, we focus on the coefficient of x (m).
Identifying Slope from the Slope-Intercept Form

The most straightforward way to find the slope is when the equation is in slope-intercept form, (y = mx + b):
- y represents the vertical position.
- x represents the horizontal position.
- m is the slope.
- b is the y-intercept, the point where the line crosses the y-axis.

💡 Note: Remember, this is the easiest form for slope identification because the slope is directly the coefficient of x.
Finding Slope from Other Equation Forms
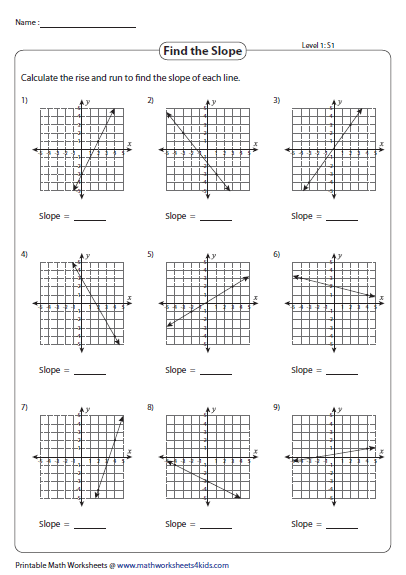
Not all equations come in slope-intercept form. Here’s how to find the slope in other common forms:
Standard Form

The standard form of a linear equation is (Ax + By = C):
- Slope is (-\frac{A}{B}).
- This form might require some manipulation to isolate y.
Point-Slope Form

The point-slope form looks like (y - y_1 = m(x - x_1)), where:
- m is still the slope.
- ((x_1, y_1)) is a point on the line.
To find the slope:
- If the equation is already in this form, the slope is m.
- If not, you need to rearrange to match this form.
Worksheet: Slope from Equation Practice

Practicing is key to mastering any concept. Here’s a worksheet to help you solidify your understanding:
Problem 1: Slope Intercept Form

Given the equation (y = \frac{2}{3}x - 4):
- Identify the slope.
Problem 2: Standard Form
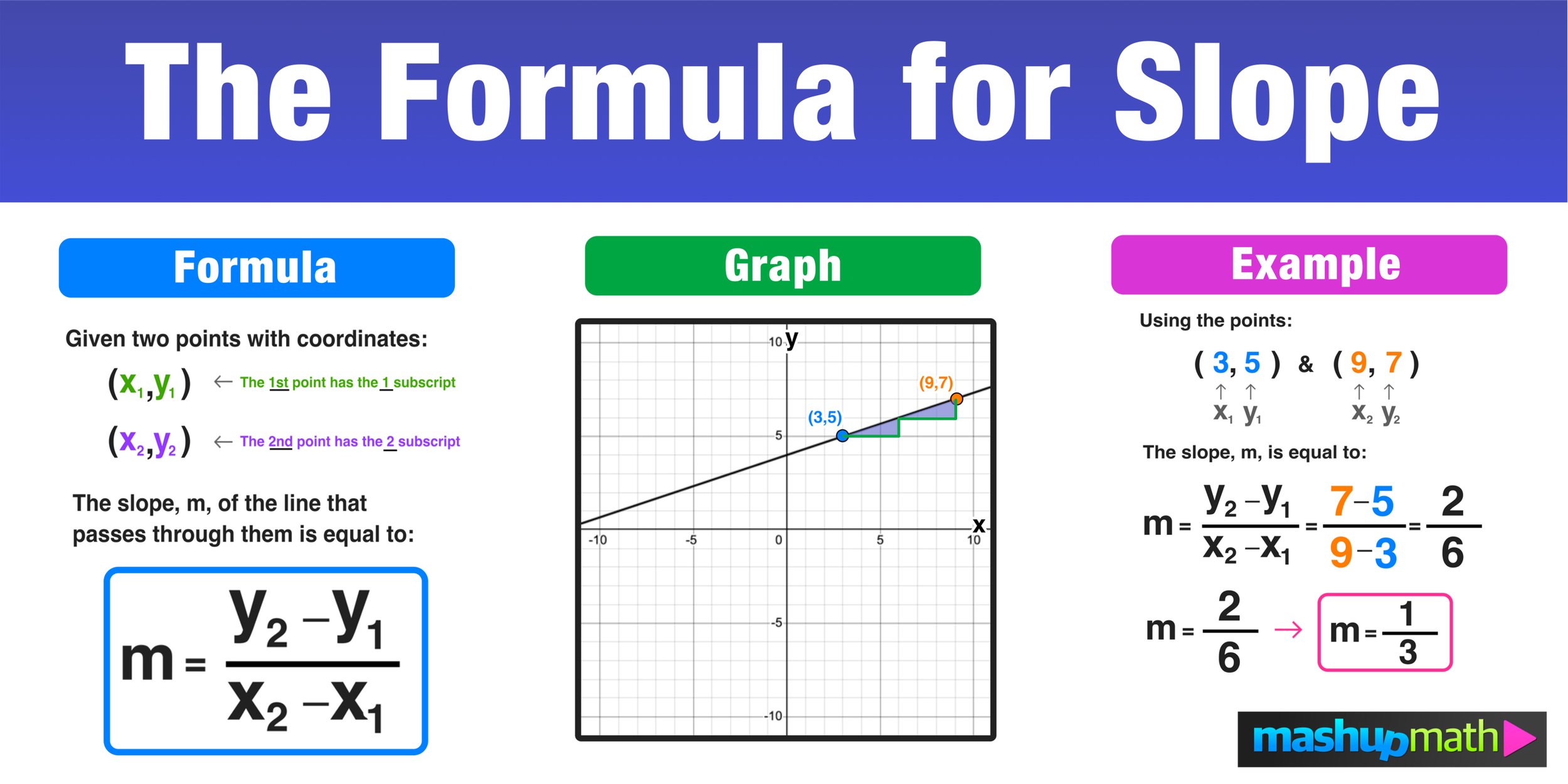
Given the equation (2x + 3y = 12):
- Find the slope by converting to slope-intercept form.
Problem 3: Point-Slope Form

Given the equation (y - 3 = 5(x - 1)):
- Identify the slope directly or after conversion to slope-intercept form.
Tips for Success

Here are some tips to streamline your slope identification:
- Always start by identifying the form of the equation.
- Isolate y when working with standard form.
- Check the sign of the slope to determine if the line rises or falls.
In summary, understanding how to find the slope from different equation forms is an essential mathematical skill. This guide has walked you through the steps to identify and calculate slope from equations in various forms, ensuring you can approach any equation with confidence. With practice and these tips, you’ll be able to solve slope-related problems efficiently and accurately.
What is the difference between slope and y-intercept?

+
The slope (m) indicates how steep the line is or the rate of change. The y-intercept (b) is where the line intersects the y-axis, or the initial value of y when x equals zero.
Can the slope be negative?

+
Absolutely, a negative slope means the line descends as x increases, indicating a decline in y-values.
Why is the slope important in real-world applications?

+
Slope helps in analyzing trends, predicting future values, and understanding relationships like speed vs. time, cost vs. quantity, etc.
How can I convert any linear equation to the slope-intercept form?

+
To convert to slope-intercept form ((y = mx + b)), solve for y by isolating it on one side of the equation. Add or subtract to get y by itself, then divide by any term left with y.
What if there’s no x in the equation?
+
If there’s no x, the line is vertical, meaning the equation (x = k) has an undefined slope, which signifies a line with no incline, or infinite steepness.