8 Ways to Master Slope from Graphs: 8th Grade Worksheet

In mathematics, understanding slope is crucial for interpreting relationships in data and functions. Slope, often represented by the letter m , indicates the steepness of a line and its direction. For 8th graders, mastering the concept of slope through various graph-based activities not only enhances their mathematical skills but also prepares them for advanced algebraic concepts. Here are eight effective strategies to excel in interpreting slope from graphs.
1. Understanding Basic Slope Definition

Before delving into graphs, make sure your students understand what slope means:
- The rise over run - how much a line goes up (or down) for each unit moved along the x-axis.
- Positive slopes go up from left to right; negative slopes go down.
- A slope of zero indicates a horizontal line, while an undefined slope represents a vertical line.
📝 Note: Students should remember the formula: ( m = \frac{\Delta y}{\Delta x} ).
2. Visualizing Slope with Grid Lines

Start with grid paper or graph paper:
- Plot points and draw lines connecting them. Highlight how the slope affects the line’s direction and steepness.
- Use the grid to count the “rise” and “run” for various lines. This hands-on approach helps in visualizing the concept.

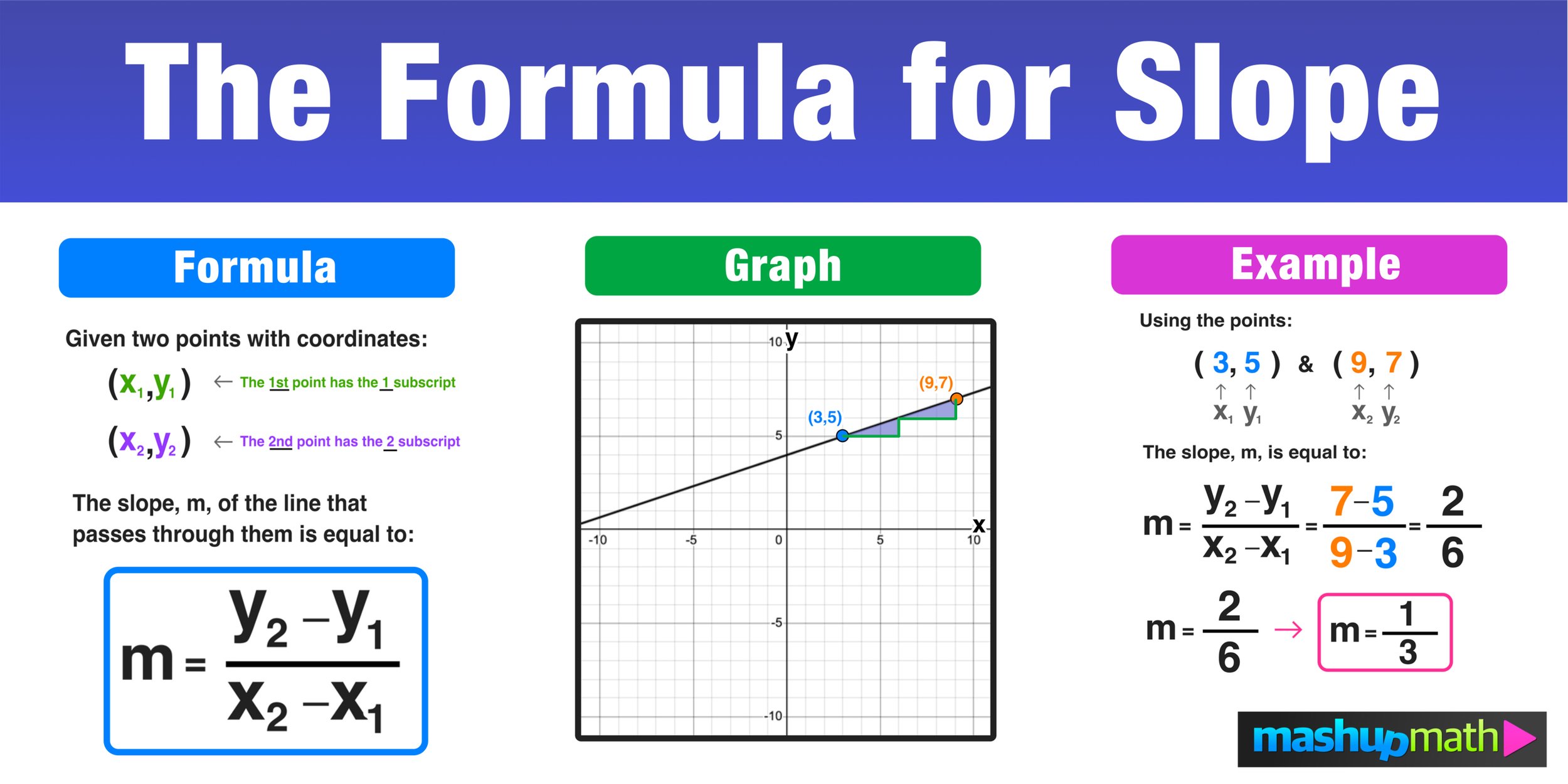
3. Slope from Two Points

Teach students to calculate slope between two points using the slope formula:
[ m = \frac{y_2 - y_1}{x_2 - x1} ]
🧮 Note: Encourage students to always start with the same point (top or bottom) to avoid confusion in calculation.
4. Recognizing Horizontal and Vertical Lines
Explain that:
- Horizontal lines have a slope of 0.
- Vertical lines have an undefined slope.
5. Graphing Lines of Different Slopes

Ask students to graph lines with the following slopes:
| Graph | Slope |
|---|---|
| Line 1 | 1 |
| Line 2 | -1 |
| Line 3 | 2 |
| Line 4 | -2 |

Discuss how each line looks different and the implications of these slopes in real-world scenarios.
6. Slope-Intercept Form Exploration

Introduce the slope-intercept form of a line:
[ y = mx + b ]
where ( m ) is the slope and ( b ) is the y-intercept. Have students:
- Identify the slope and y-intercept from a given equation.
- Sketch the line on a graph paper.
7. Comparing Slopes in Real-Life Contexts

Relate slopes to everyday scenarios:
- Discuss how a steep slope might represent a steep hill or a rapidly increasing rate of change.
- Contrast it with a gentle slope representing a gradual change.
8. Interactive Slope Activities
Engage students with dynamic learning tools:
- Use interactive graph software where students can manipulate the slope and observe the effects immediately.
- Incorporate real-world data sets or experiments where students can calculate slopes to make predictions or analyze trends.

By employing these eight techniques, students can develop a thorough understanding of slope. From visualizing the steepness through grid lines to applying slopes to real-life scenarios, each method reinforces the concept in a unique way. This well-rounded approach ensures students not only grasp the mathematical formulas but also appreciate the practical applications of slope, setting a solid foundation for higher-level mathematics.
What does the slope of a horizontal line indicate?

+
A horizontal line has a slope of zero, indicating no change in the y-coordinate as the x-coordinate increases.
Can the slope of a line be negative?

+
Yes, a negative slope indicates that the line slopes downward from left to right. It means that for every unit increase in (x), (y) decreases.
How can understanding slope help in real life?

+
Understanding slope can help in numerous scenarios like analyzing the growth rate of populations, determining the incline of ramps for accessibility, predicting weather patterns, or evaluating financial investments for gains or losses over time.