5 Ways to Solve Missing Angles Easily

Geometry is one of those subjects where accuracy and precision in calculations are non-negotiable. Whether you're a student struggling with geometry homework, a professional designer, or simply someone trying to figure out the right angles for a DIY project, knowing how to solve missing angles is crucial. This guide will explore 5 effective methods to tackle this common geometric puzzle, ensuring that you can find the right angle every time.
1. Using Geometry Theorems
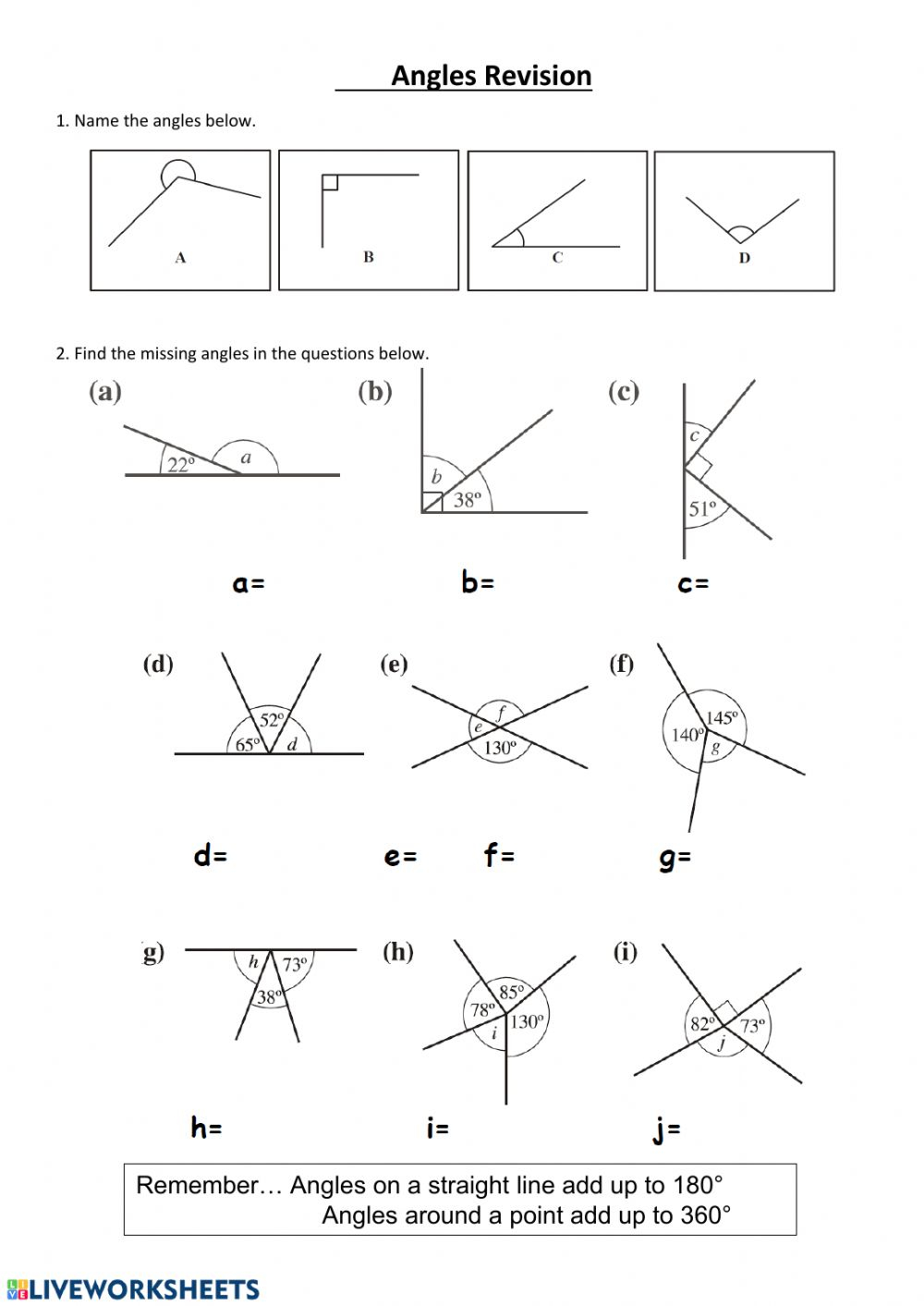
Before diving into any calculations, understanding the basic geometry theorems can simplify your task significantly:
- Sum of Angles in a Triangle: The total sum of internal angles in any triangle always equals 180 degrees. If you know two angles, subtract their sum from 180 to find the third angle.
- Complementary Angles: Two angles are complementary if their sum equals 90 degrees.
- Supplementary Angles: These angles sum to 180 degrees.
- Vertical Angles: When two lines intersect, the angles opposite each other are equal.
🎯 Note: Before applying these theorems, ensure you identify the correct types of angles involved in your problem to choose the right theorem.
2. The Right Triangle Approach

For right triangles (where one angle is 90 degrees), you can use:
- Pythagorean Theorem: If you know two sides, you can find the third using a^2 + b^2 = c^2.
- Trigonometric Functions: Use sin, cos, or tan to find unknown angles when sides are known. For example:
- Sin(θ) = Opposite/Hypotenuse
- Cos(θ) = Adjacent/Hypotenuse
- Tan(θ) = Opposite/Adjacent
✅ Note: Ensure to use the correct trigonometric function based on which sides you know relative to the unknown angle.
3. Using Parallel Lines
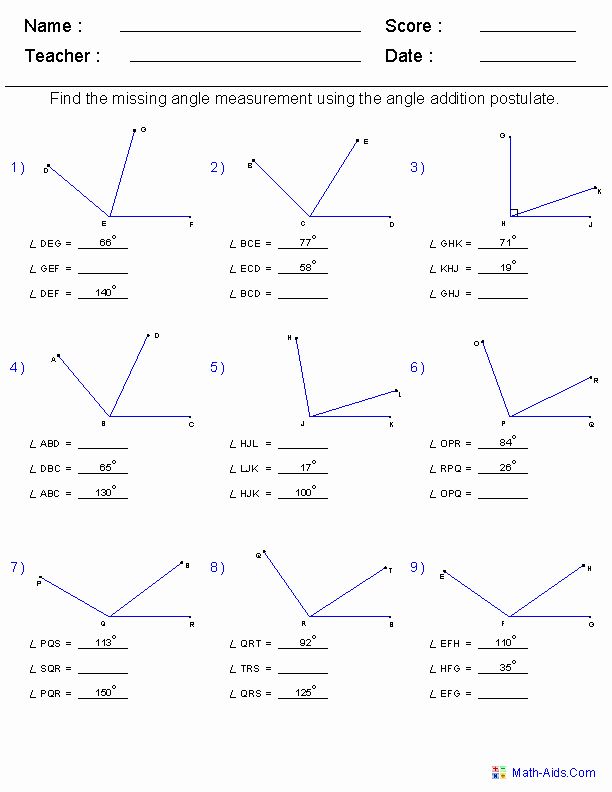
When you have parallel lines cut by a transversal:
- Alternate Interior Angles: These angles are equal.
- Corresponding Angles: Angles in matching corners are equal.
- Consecutive Interior Angles: These angles sum to 180 degrees.
🌱 Note: Practice identifying these angles as recognizing them can simplify solving for missing angles.
4. Similar Triangles

If you identify triangles as similar:
- The corresponding sides are proportional, allowing you to set up ratios and solve for unknown sides or angles.
- AA (Angle-Angle) Similarity Postulate: If two triangles have two pairs of corresponding angles equal, they are similar.
| Angle 1 | Angle 2 | Angle 3 |
|---|---|---|
| 70° | 60° | 50° |
| 45° | 90° | 45° |

📈 Note: This method is particularly useful when you have multiple angles to calculate.
5. Sum Method

When multiple polygons meet or intersect:
- Sum of Angles in Polygons: You can use the formula (n-2) * 180 where n is the number of sides of the polygon.
- Subtract known angles from this sum to find the missing angles.
- External Angles: In any polygon, each external angle plus its adjacent internal angle equals 180 degrees.
💡 Note: This method is versatile and can be applied to any polygon, not just triangles.
The key to mastering geometry is not just memorizing formulas but understanding the relationships between angles and shapes. Each of these methods has its strengths, and by combining them, you can solve almost any problem involving missing angles. Remember, accuracy in initial measurements and calculations will significantly impact your results.
What are the simplest ways to check if I’ve calculated angles correctly?

+
Use the sum method for triangles or polygons. If the sum of the angles equals 180 degrees (for triangles) or follows the polygon formula, your calculation is likely correct.
Can I use a protractor instead of these methods?

+
Yes, but these methods are more precise for complex problems and can help verify protractor measurements.
How do I find an angle in a quadrilateral when only one angle is given?

+
Use the fact that the sum of the interior angles in a quadrilateral is 360 degrees to solve for unknown angles.