5 Ways to Find Missing Angles in Triangles Easily

Understanding Angles in Triangles

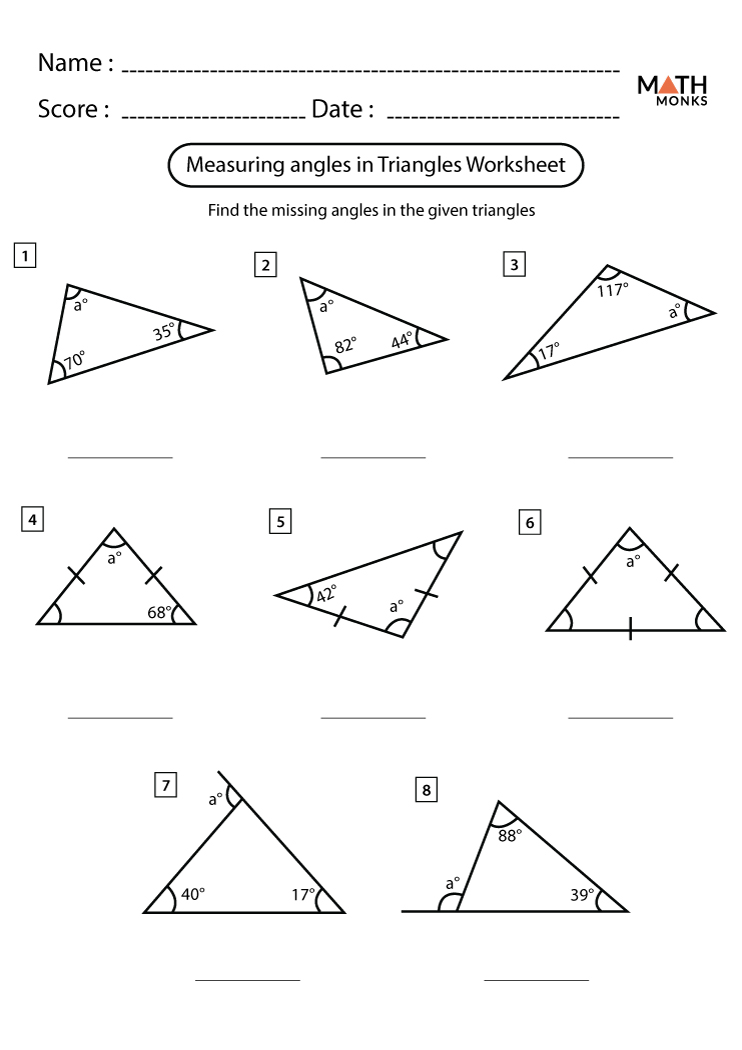
Triangles are one of the most basic shapes in geometry, consisting of three sides and three angles. The sum of the interior angles of a triangle is always 180 degrees. This fundamental property makes it easy to find missing angles in triangles, as long as you know the measurements of the other angles. In this article, we will explore five methods to find missing angles in triangles easily.
Method 1: Using the Sum of Interior Angles Property

The most straightforward way to find a missing angle in a triangle is to use the sum of interior angles property. This property states that the sum of the three interior angles of a triangle is always 180 degrees. To use this method, simply add up the measurements of the two known angles and subtract the result from 180 degrees.
🤔 Note: This method assumes that you know the measurements of two angles in the triangle.
For example, let’s say we have a triangle with angles A, B, and C. We know that angle A is 60 degrees and angle B is 80 degrees. To find the measurement of angle C, we can use the following equation:
A + B + C = 180
Substituting the values of A and B, we get:
60 + 80 + C = 180
Simplifying the equation, we get:
140 + C = 180
Subtracting 140 from both sides, we get:
C = 40
Therefore, the measurement of angle C is 40 degrees.
Method 2: Using the Exterior Angle Theorem

The exterior angle theorem states that the exterior angle of a triangle is equal to the sum of the two opposite interior angles. This theorem can be used to find missing angles in triangles.
For example, let’s say we have a triangle with angles A, B, and C. We know that angle A is 60 degrees and the exterior angle opposite to angle A is 120 degrees. To find the measurement of angle B, we can use the following equation:
Exterior angle = A + B
Substituting the values, we get:
120 = 60 + B
Simplifying the equation, we get:
60 = B
Therefore, the measurement of angle B is 60 degrees.
Method 3: Using the Alternate Interior Angles Theorem
The alternate interior angles theorem states that if two lines intersect a third line, then the alternate interior angles are equal. This theorem can be used to find missing angles in triangles.
For example, let’s say we have a triangle with angles A, B, and C. We know that angle A is 60 degrees and angle B is 80 degrees. We also know that the two lines intersecting the third line form an angle of 60 degrees. To find the measurement of angle C, we can use the following equation:
A = Alternate interior angle
Substituting the values, we get:
60 = Alternate interior angle
Since the alternate interior angle is equal to angle C, we can conclude that angle C is also 60 degrees.
Method 4: Using the Corresponding Angles Theorem

The corresponding angles theorem states that if two lines intersect a third line, then the corresponding angles are equal. This theorem can be used to find missing angles in triangles.
For example, let’s say we have a triangle with angles A, B, and C. We know that angle A is 60 degrees and the corresponding angle is 80 degrees. To find the measurement of angle B, we can use the following equation:
A = Corresponding angle
Substituting the values, we get:
60 = 80
Since the corresponding angle is equal to angle B, we can conclude that angle B is also 80 degrees.
Method 5: Using the Angle Sum Property of Quadrilaterals

This method involves extending one side of the triangle to form a quadrilateral. The angle sum property of quadrilaterals states that the sum of the interior angles of a quadrilateral is 360 degrees. This property can be used to find missing angles in triangles.
For example, let’s say we have a triangle with angles A, B, and C. We know that angle A is 60 degrees and angle B is 80 degrees. To find the measurement of angle C, we can extend side AB to form a quadrilateral. Let’s call the new angle formed angle D. We can use the following equation:
A + B + C + D = 360
Substituting the values, we get:
60 + 80 + C + D = 360
Simplifying the equation, we get:
140 + C + D = 360
Subtracting 140 from both sides, we get:
C + D = 220
Since angle D is an exterior angle of the triangle, it is equal to the sum of the two opposite interior angles. Therefore, we can write:
D = A + B
Substituting the values, we get:
D = 60 + 80
D = 140
Substituting the value of D into the previous equation, we get:
C + 140 = 220
Subtracting 140 from both sides, we get:
C = 80
Therefore, the measurement of angle C is 80 degrees.
In conclusion, finding missing angles in triangles can be easy and straightforward using one of the five methods described above. Whether you use the sum of interior angles property, the exterior angle theorem, the alternate interior angles theorem, the corresponding angles theorem, or the angle sum property of quadrilaterals, you can be confident in your ability to find missing angles in triangles.
What is the sum of interior angles in a triangle?

+
The sum of interior angles in a triangle is always 180 degrees.
What is the exterior angle theorem?

+
The exterior angle theorem states that the exterior angle of a triangle is equal to the sum of the two opposite interior angles.
What is the alternate interior angles theorem?

+
The alternate interior angles theorem states that if two lines intersect a third line, then the alternate interior angles are equal.
Related Terms:
- interior exterior angles triangles worksheet
- missing angles in triangles printable
- triangle exterior angle theorem worksheet
- triangle angles worksheet grade 6
- finding exterior angle triangle worksheet
- calculating angles in triangles worksheet