Area of Shapes Worksheet: Fun Geometry Practice
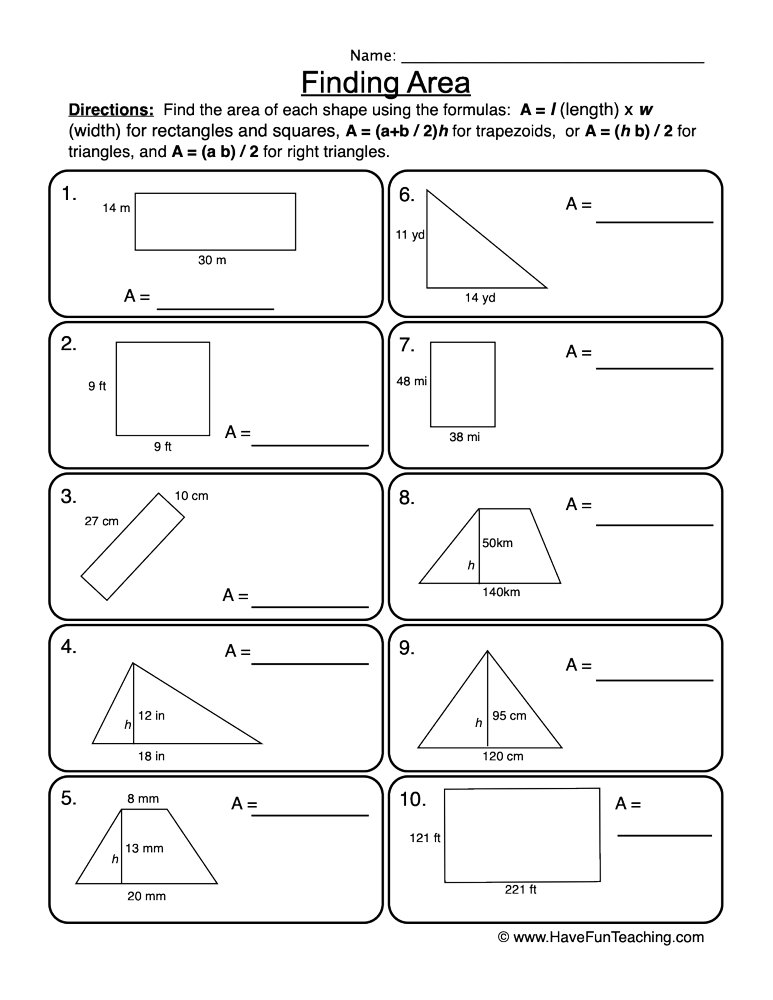
In the world of geometry, understanding the formulas for calculating areas of different shapes is not only fundamental but also quite fascinating. This comprehensive guide dives into various geometric shapes, providing a playful yet educational journey through the world of shapes, their formulas, and practical exercises designed to enhance your knowledge.
Introduction to Basic Shapes

The study of geometry begins with the simplest forms: the square, rectangle, triangle, and circle. Here, we explore their basic properties:
- Square: A square has all sides of equal length and all angles are 90 degrees. The area of a square can be calculated by
A = side². - Rectangle: Like a square but with different lengths for its adjacent sides. Its area formula is
A = length × width. - Triangle: With its three sides, a triangle's area is given by
A = (base × height) / 2. - Circle: Known for its circular symmetry, its area formula is
A = πr², whereris the radius.
📐 Note: Remember, π (pi) is approximately 3.14159 for practical calculations.
Area Calculation: Practice Worksheets

Let's jump into some hands-on practice with these shapes:
Worksheet 1: Squares and Rectangles

Here's a table for quick area calculation of squares and rectangles:
| Shape | Dimensions | Area Formula |
|---|---|---|
| Square | Side = 5 cm | A = 5² = 25 cm² |
| Rectangle | Length = 7 cm, Width = 3 cm | A = 7 × 3 = 21 cm² |

🔍 Note: Practice calculating these areas to strengthen your understanding of basic shape dimensions.
Worksheet 2: Triangles

Calculate the area for these triangles:
- A triangle with base = 8 cm and height = 5 cm. (
A = (8 × 5) / 2 = 20 cm²) - Another triangle with base = 12 cm and height = 3 cm. (
A = (12 × 3) / 2 = 18 cm²)
Worksheet 3: Circles

Find the area of circles with the following radii:
- Radius = 4 cm. (
A = π × 4² ≈ 50.27 cm²) - Radius = 3 cm. (
A = π × 3² ≈ 28.27 cm²)
Advanced Shapes and Their Areas
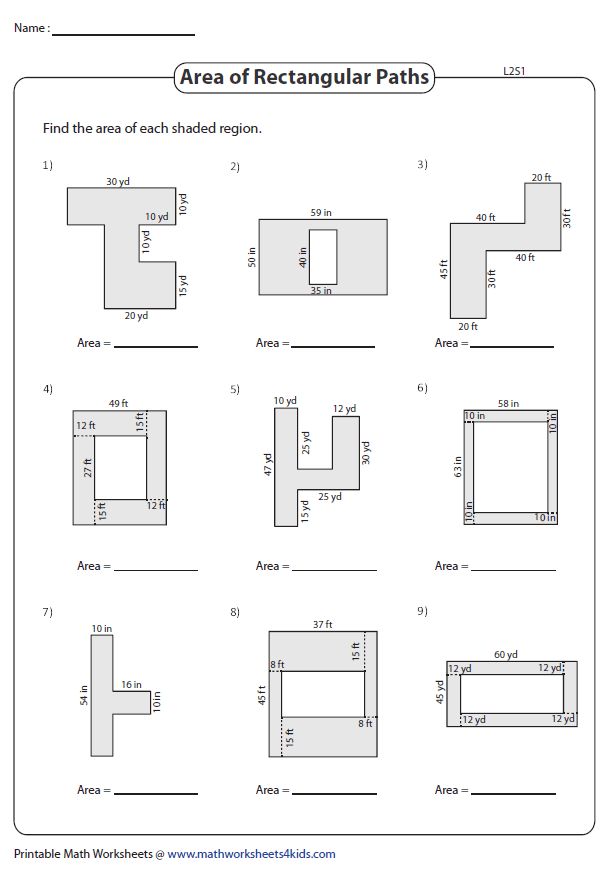
Now, let's explore a few more complex shapes:
Parallelogram

A parallelogram has opposite sides that are equal in length and parallel, with area given by A = base × height.
Trapezium

A trapezium or trapezoid has one pair of parallel sides. Its area is calculated using A = (sum of parallel sides) / 2 × height.
Rhombus

A rhombus is a special case of a parallelogram where all sides are equal. The area can be found in two ways: A = (d₁ × d₂) / 2, where d₁ and d₂ are the lengths of the diagonals.
Final Thoughts

Geometry isn't just about shapes; it's about how these shapes relate to our world, from the design of buildings to the engineering of bridges, from the pattern of a leaf to the stars in the sky. By mastering the basics of area calculation, you've equipped yourself with a tool that extends far beyond the classroom into everyday applications. Whether you're pursuing a career in design, architecture, or just enjoying math for the sake of curiosity, the knowledge of shape areas is invaluable.
What are some real-world applications of area calculation?

+
From urban planning, where land area calculations are crucial for zoning, to home improvement projects where calculating room area helps in estimating flooring or painting needs, area calculation plays a pivotal role. Even in gardening, knowing the area helps in determining how much soil or seeds you’ll need for a garden bed.
How can I remember all these formulas?

+
One effective way is through mnemonics, associating each shape with something memorable or visualizing the shapes and their components. Regular practice, integrating the formulas into real-life scenarios, and teaching others can also reinforce memory.
Is there a quick way to estimate the area of an irregular shape?

+
Yes, one common method is the “dot grid” technique where you overlay a grid of dots onto the shape and count how many dots are inside it. Estimating the area then becomes a matter of simple counting and division, although it might not be as accurate as formal calculations for precise needs.