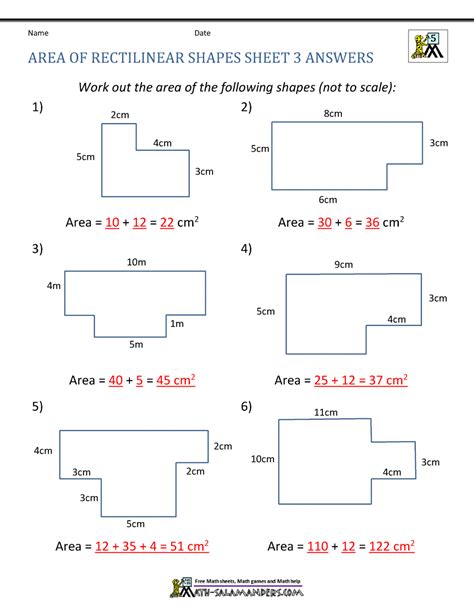
Irregular Shapes Area Worksheet With Answers and Solutions
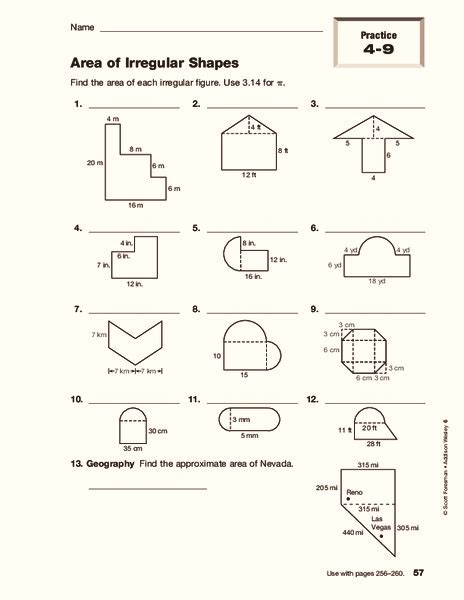
Understanding Irregular Shapes and Calculating Their Areas

When dealing with shapes that don’t fit into the standard categories of squares, rectangles, triangles, and circles, we enter the realm of irregular shapes. These shapes can be a combination of various regular shapes or completely random, making calculations such as area and perimeter a bit more complex. In this worksheet, we’ll explore how to calculate the areas of irregular shapes using different strategies and provide solutions to exercises.
What are Irregular Shapes?

Irregular shapes are polygons or figures that do not have equal sides or angles. Unlike regular shapes, where we can easily calculate the area using specific formulas (e.g., Area = side^2 for squares), irregular shapes require breaking down into recognizable parts or using more general approaches.
Methods for Calculating the Area of Irregular Shapes
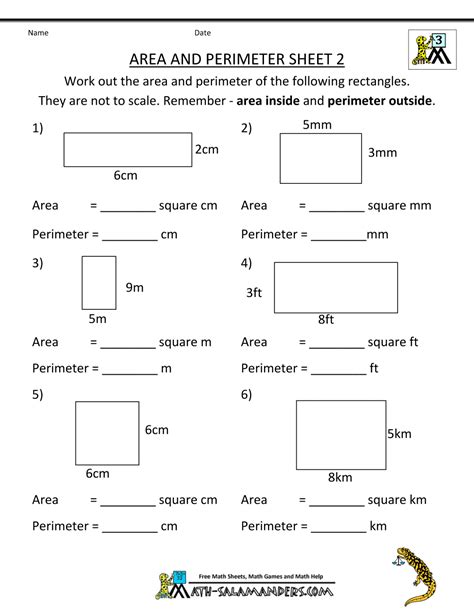
1. Divide into Recognizable Shapes
One of the simplest methods to calculate the area of an irregular shape is to divide it into recognizable shapes such as squares, triangles, or rectangles, and then sum the areas of these shapes.
2. Use of Grids

Another method is to superimpose a grid over the shape and count the number of squares or triangles formed by the grid that are either fully or partially inside the shape. The total area is then calculated by adding up the areas of these grid squares or triangles.
3. Apply Formulas for Regular Shapes

If the irregular shape can be dissected into regular shapes for which we have area formulas, we can apply these formulas to find the total area.
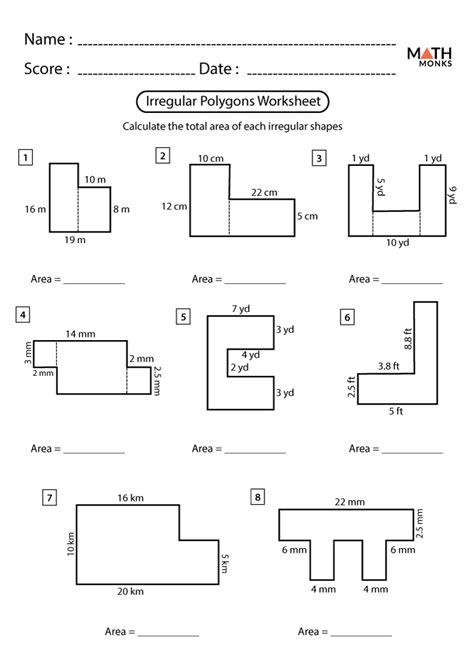
4. Polygon Decomposition

For complex shapes, decomposing them into simpler polygons like triangles and rectangles can make the calculation easier.
Examples and Solutions

Example 1: Irregular Shape Decomposition into Rectangles and Triangles

| Shape Part | Length (cm) | Width (cm) | Area (cm^2) |
|---|---|---|---|
| Rectangle 1 | 4 | 3 | 12 |
| Rectangle 2 | 2 | 5 | 10 |
| Triangle | Base: 3, Height: 4 | - | 6 |
| Total Area | - | - | 28 |
Solution: The total area of the irregular shape is the sum of the areas of the two rectangles and the triangle, which equals 28 cm^2.
📝 Note: Always ensure the units are consistent when adding areas.
Example 2: Using a Grid to Approximate Area
Suppose we have an irregular shape superimposed on a 1 cm by 1 cm grid. After counting, we find that the shape covers 15 full squares, 6 half-squares, and 2 quarter-squares.
Solution: The area covered by full squares is 15 cm^2, by half-squares is 3 cm^2 (since 6 halves equal 3 wholes), and by quarter-squares is 0.5 cm^2 (since 2 quarters equal 0.5 wholes). Therefore, the total area is approximately 18.5 cm^2.
Practice Exercises
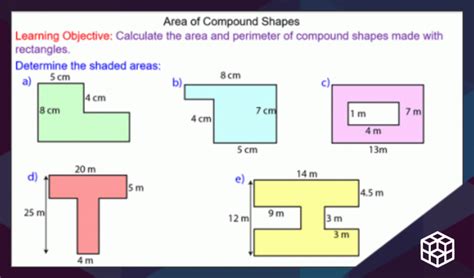
Dissected Shape: A shape is divided into a 4 cm by 5 cm rectangle and a right-angled triangle with a base of 3 cm and a height of 4 cm. Calculate the total area.
Grid Overlay: An irregular shape covers 20 full squares, 4 half-squares, and 1 quarter-square on a 1 cm by 1 cm grid. Calculate the approximate area.
Polygon Breakdown: Break down the complex shape shown below into simpler shapes and calculate its total area.
How do I calculate the area of an irregular shape if it can't be broken down into simpler shapes?
+For complex shapes that cannot be easily divided into simpler shapes, using a grid overlay can provide a reasonable approximation of the area.
What if the shape has curves? Can I still use these methods?
+For shapes with curves, approximations can be made by breaking the shape into parts that can be more easily calculated, or using calculus for more precise calculations.
How accurate are these methods for calculating the area of irregular shapes?
+The accuracy depends on the method used. Breaking down into simpler shapes provides exact areas, while using grids offers approximations that can be as accurate as needed by increasing the grid's precision.
Understanding and calculating the areas of irregular shapes can be challenging but also rewarding. By applying the strategies outlined here, you’ll be able to tackle a wide range of problems involving these shapes, from basic exercises to real-world applications. Remember, the key is to understand the shape’s components and apply the appropriate method to calculate its area accurately.



