Unlock Parallelogram Answers: Measure and Master Your Skills
Unlocking the mysteries of parallelograms can be a rewarding journey into the realm of geometry, whether you're a student learning new shapes or a professional looking to hone your drafting skills. The unique properties and characteristics of parallelograms make them fascinating subjects for mathematical exploration and practical application. This comprehensive guide will help you master everything there's to know about measuring and understanding parallelograms, turning you into a true expert in this geometric figure.
Understanding the Basics of Parallelograms

A parallelogram is a quadrilateral with two pairs of parallel sides. Here's what you need to know to grasp its fundamental nature:
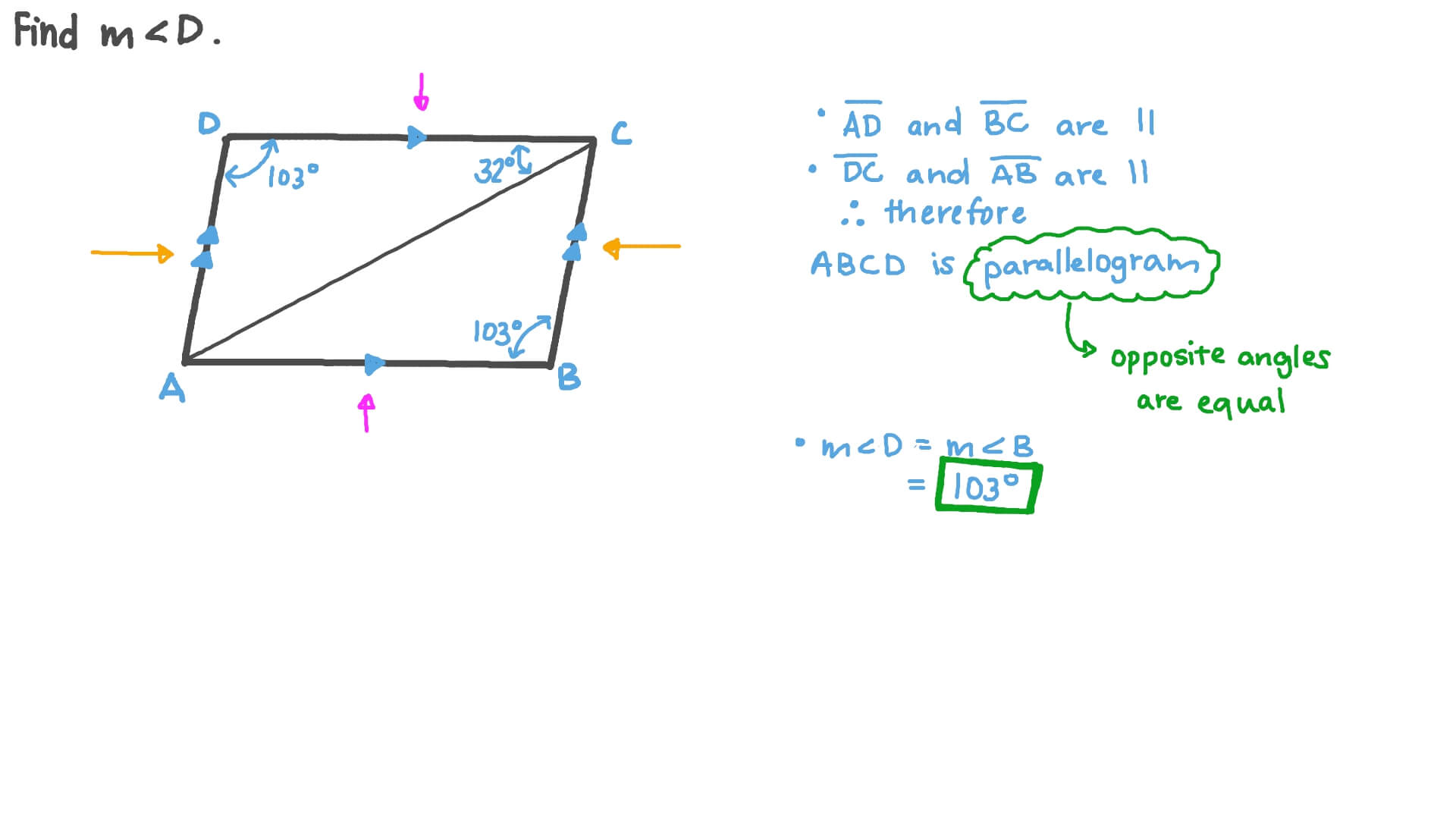
- Opposite Sides: They are equal in length and parallel to each other.
- Opposite Angles: They are equal, and adjacent angles sum up to 180 degrees.
- Diagonals: They bisect each other.
How to Measure a Parallelogram

Here’s a step-by-step guide on how to accurately measure a parallelogram:
Step 1: Identify the Dimensions

Find the length of one side and one height or base, which are typically perpendicular to each other.
Step 2: Calculate the Area

The formula for the area of a parallelogram is:
A = b * h
where b is the base, and h is the height.
Step 3: Compute the Perimeter

To calculate the perimeter, use:
P = 2(b + s)
where s is the length of one side (not the base).
Step 4: Understanding Diagonals

Each diagonal of a parallelogram divides it into two congruent triangles, and the length of the diagonals can be calculated using the law of cosines or Pythagorean theorem if the base and height are known.
⚠️ Note: When measuring for angles, ensure your protractor is properly aligned with the base or side to get an accurate angle measurement.
Applying Parallelogram Knowledge

Let’s delve into some practical applications of parallelograms:
- Architecture: Parallelograms can be found in floor plans, roof structures, and window designs.
- Design and Art: They are used in tiling patterns, textile design, and optical illusions.
- Engineering: Parallelograms can represent force diagrams or help in calculating cross-sections of beams.
Common Mistakes to Avoid

When dealing with parallelograms, here are some common pitfalls to watch out for:
- Confusing parallelograms with rectangles or squares by not recognizing the distinct properties.
- Neglecting to verify that opposite sides are parallel.
- Not correctly identifying the height perpendicular to the base.
What's the difference between a rectangle and a parallelogram?

+
A rectangle has all right angles, whereas a parallelogram has two pairs of parallel sides, but the angles are not necessarily right angles.
How can you tell if a shape is a parallelogram?

+
You can identify a parallelogram by checking that both pairs of opposite sides are parallel and equal in length, and opposite angles are equal.
Can the area of a parallelogram change if its angles change?

+
No, the area of a parallelogram is determined by the base and height, not by its angles. As long as base and height remain constant, the area stays the same.
Understanding parallelograms is a vital part of geometric education, and the ability to measure, calculate, and apply their properties can greatly enhance one’s understanding of space, form, and design. From the simple act of finding their area to recognizing them in everyday objects, mastering parallelograms opens up a world of mathematical beauty and practical applications. The key points to remember include: their unique properties, how to accurately measure them, common mistakes to avoid, and practical applications in various fields. By deepening your knowledge, you empower yourself to approach geometric problems with confidence and precision, making complex calculations more manageable and intriguing. Let’s continue exploring this fascinating geometric figure and keep our minds open to the elegance it brings to the study of shapes.