5 Steps to Master Slope Calculation with Two Points

In mathematics, understanding the slope of a line is crucial not only in geometry but also in physics, economics, and a plethora of other disciplines where changes in relationships are analyzed. The slope essentially tells us how steep a line is or the rate of change between two points. Whether you're preparing for an exam or looking to enhance your analytical skills, mastering how to calculate the slope using two points is foundational. Here, we'll walk through the five steps to calculate slope accurately and efficiently.
Step 1: Identify the Coordinates of the Two Points

The first step in finding the slope is to have two points on a line. These points are generally presented as coordinates in the form ((x_1, y_1)) and ((x_2, y_2)). For example, if you have the points (3, 4) and (6, 8), then:
- (x_1 = 3)
- (y_1 = 4)
- (x_2 = 6)
- (y_2 = 8)
📌 Note: Always ensure that the coordinates are distinct; otherwise, the slope is undefined for vertical lines.
Step 2: Understand the Slope Formula
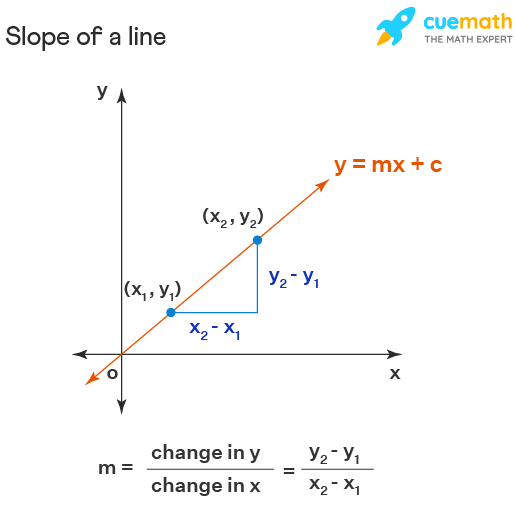
The formula to find the slope (m) between two points is given by:
[ m = \frac{y_2 - y_1}{x_2 - x_1} ]This formula represents the ratio of the vertical change (rise) to the horizontal change (run) between the two points.
Step 3: Plug in the Values
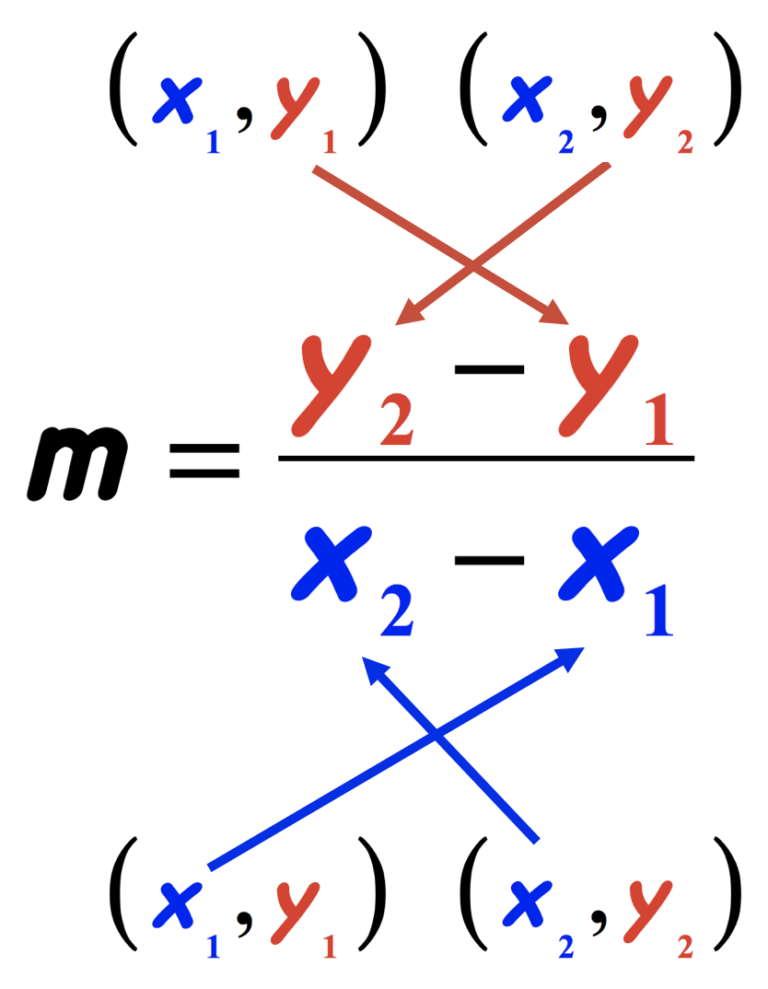
Using the example from Step 1:
[ m = \frac{8 - 4}{6 - 3} ]Step 4: Calculate the Slope
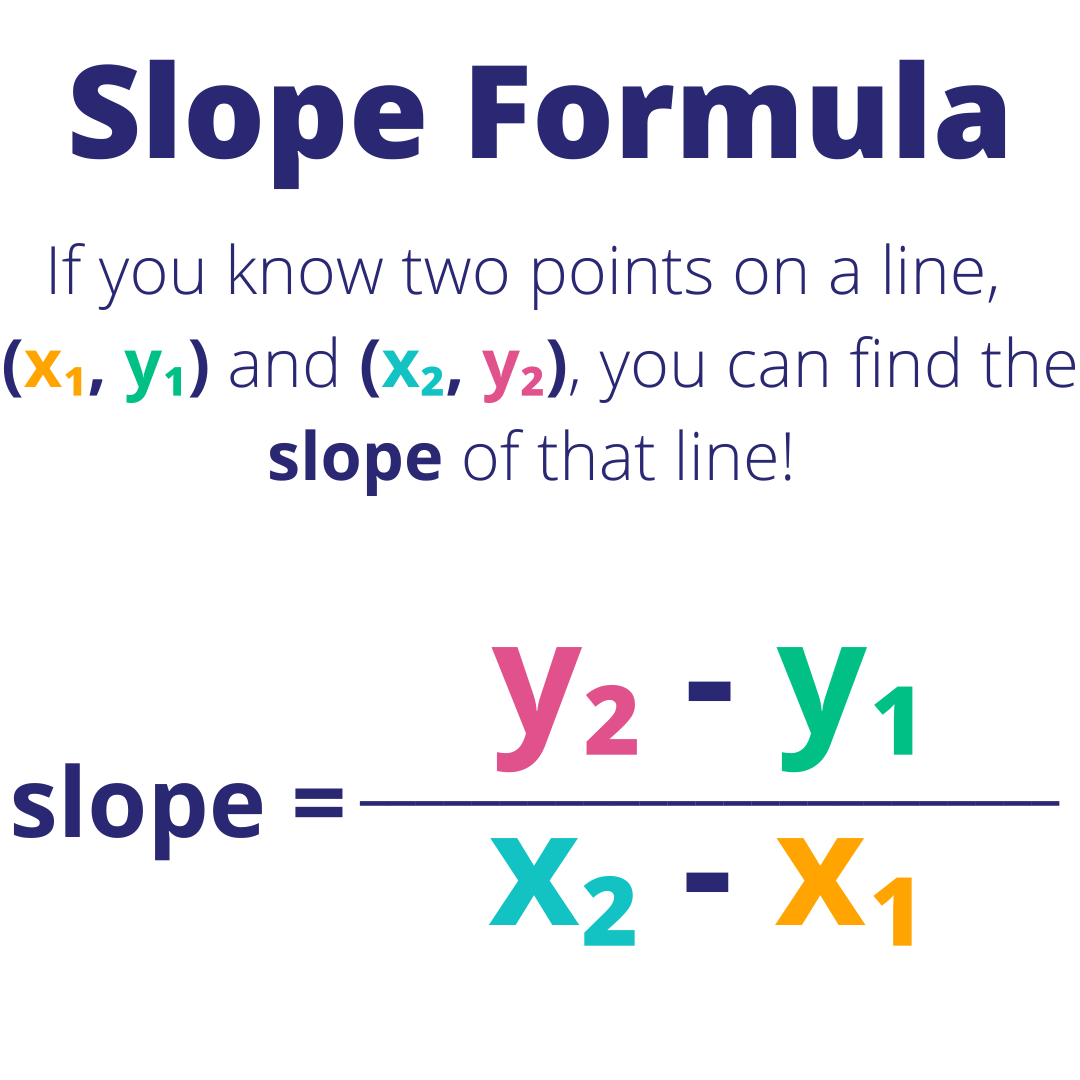
Perform the arithmetic operations:
[ m = \frac{4}{3} = 1.33 ]This calculation yields a positive slope, indicating an upward trend from left to right on the Cartesian plane.
Step 5: Interpret the Result

Interpreting the slope:
- A positive slope means the line ascends from left to right.
- A negative slope indicates a downward trend.
- Zero slope signifies a horizontal line.
- An undefined slope refers to a vertical line.
The ability to calculate slope gives you insight into the nature of the relationship between two variables. For instance, in economics, a positive slope might represent an increase in demand with price, while a negative slope could indicate the inverse relationship in the law of demand. It's a skill that transcends basic math and finds application in real-world scenarios.
While the formula seems straightforward, mastering slope calculation involves understanding the implications of the result. Slope doesn't just tell you how steep a line is; it can help predict trends, analyze data, and even forecast future outcomes. This foundational knowledge in algebra prepares you for more advanced topics like linear regression, calculus, and beyond.
Whether you're graphing lines, analyzing trends, or solving real-world problems, knowing how to calculate the slope effectively opens up numerous avenues in both academic and practical settings. Remember, practice is key. The more you work with different pairs of points, the more intuitive this process will become. So, next time you encounter two points on a plane, remember these five steps, apply them, and sharpen your analytical prowess!
What does a zero slope indicate?
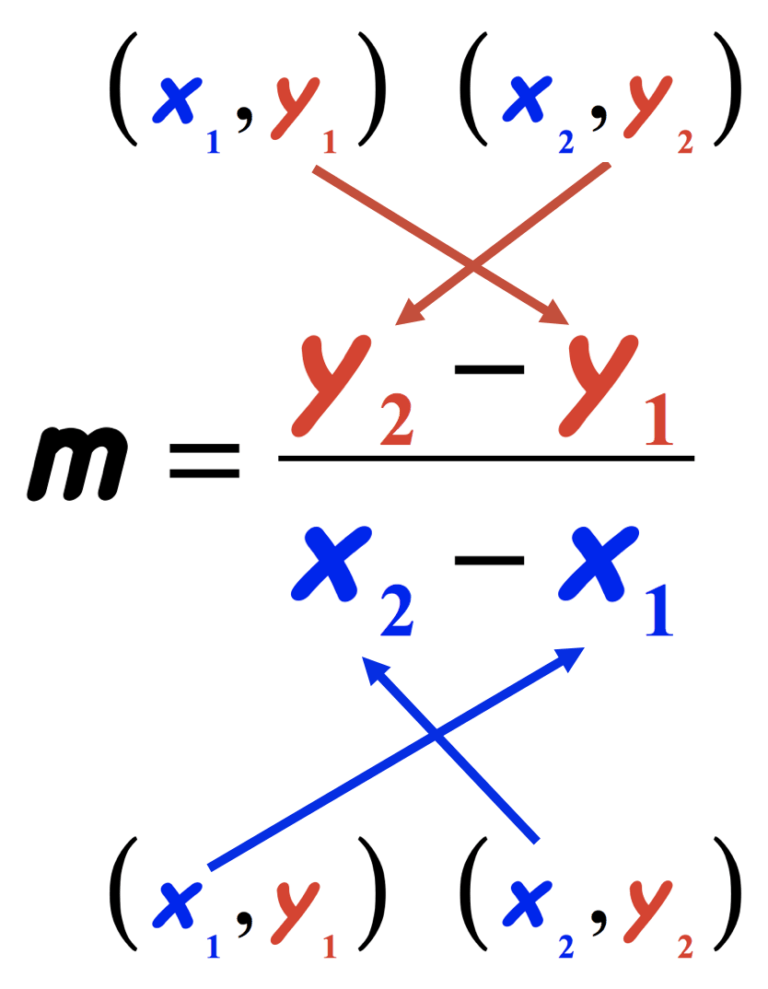
+
A zero slope indicates that the line is horizontal, and there’s no change in (y) as (x) changes.
How do I know if my slope calculation is correct?
+
Verify your calculation by plotting the points on graph paper and ensuring the line matches the calculated slope.
Can the slope be undefined?
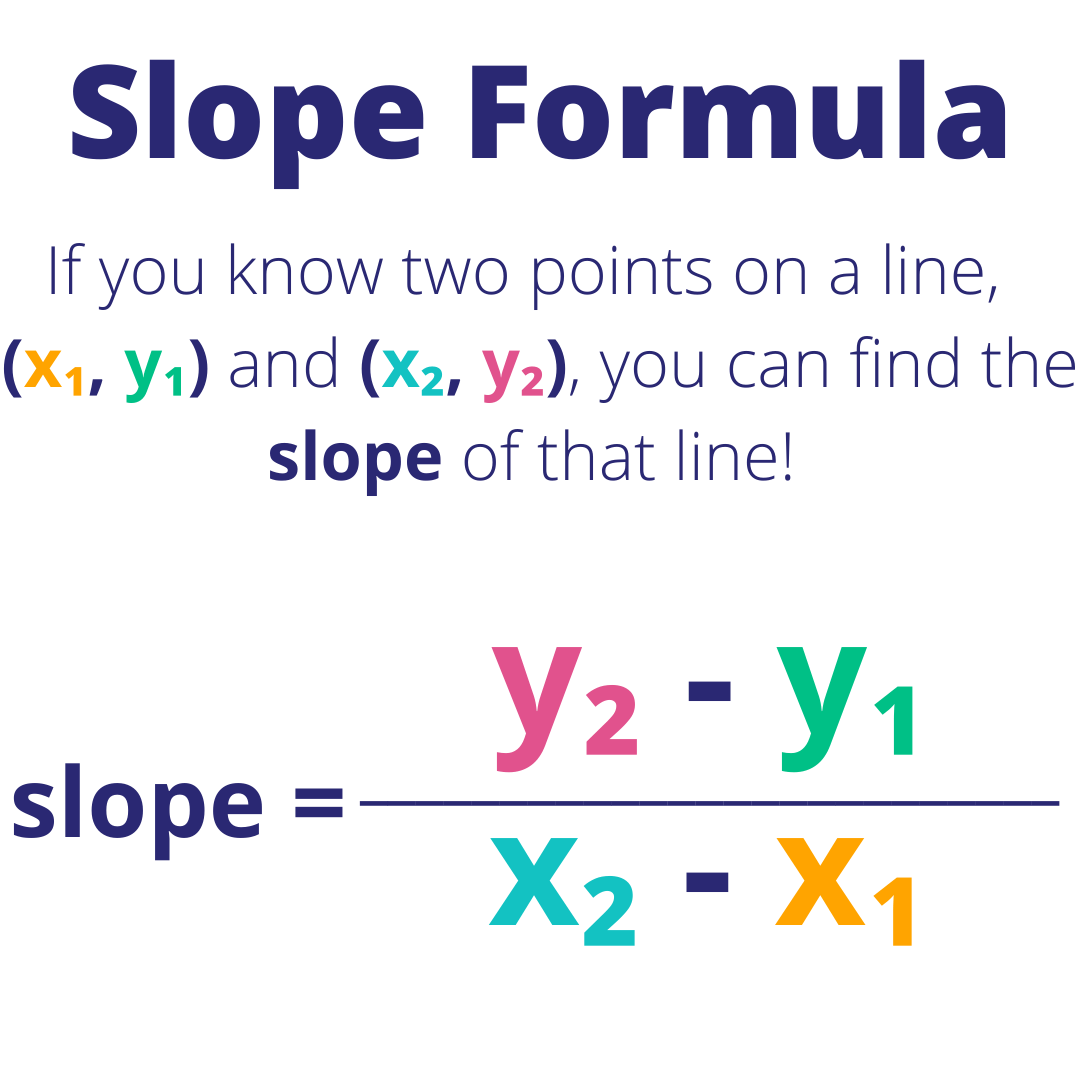
+
Yes, the slope is undefined for vertical lines because the denominator in the slope formula becomes zero, which makes the slope infinite.