5 Easy Ways to Find Slope From Graphs

When you are presented with a graph of a line, understanding its slope is essential for many mathematical and real-world applications. Slope is essentially the measure of how steep a line is. It indicates the rate at which the line rises or falls as you move from left to right on the graph. Here are five straightforward methods to determine the slope of a line from its graph:
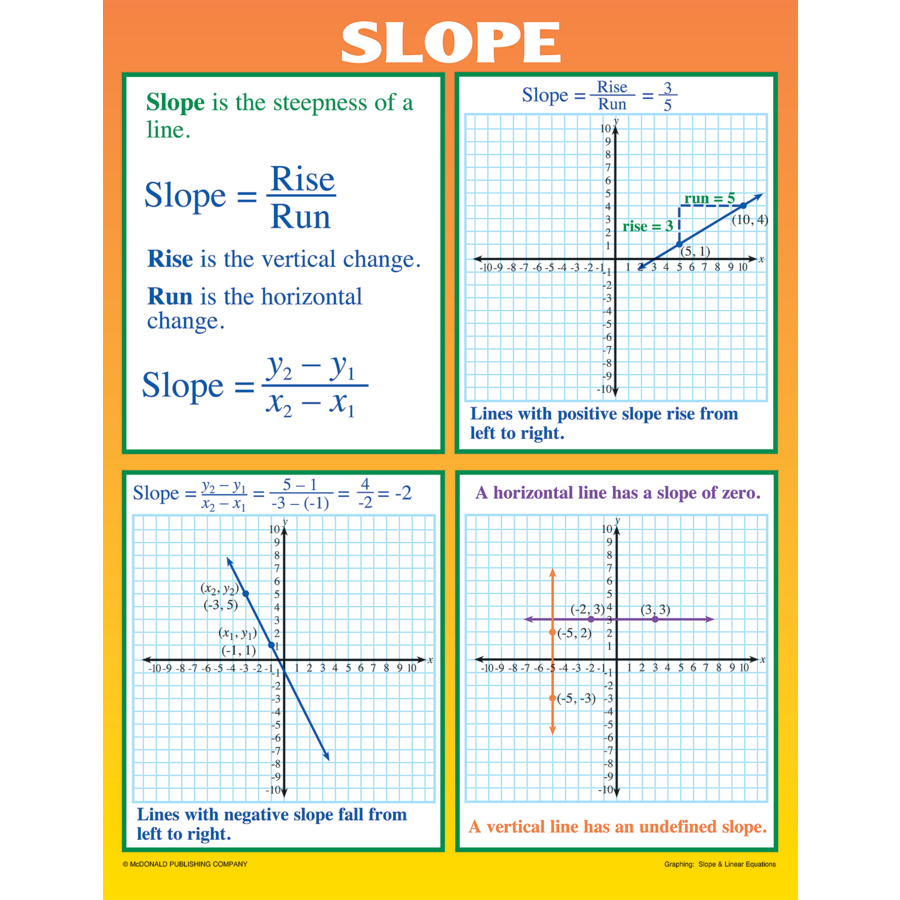
1. Using the Rise Over Run Formula

The most fundamental and well-known method for finding the slope of a line is by using the “rise over run” formula. Here’s how you can do it:
- Identify two points: Choose two distinct points on the line where you can easily see both the vertical and horizontal distances.
- Calculate the rise: Count the units the line moves vertically from the first point to the second. If the line goes up, this value is positive; if it goes down, it’s negative.
- Calculate the run: Count the units the line moves horizontally from the first point to the second.
- Apply the formula: Slope (m) = Rise / Run
📌 Note: Always remember to measure from left to right for the run and top to bottom for the rise to ensure correct calculations.
2. Utilizing the Incline Angle

If you have a protractor or know trigonometry, you can use the angle the line makes with the horizontal:
- Measure the angle between the line and the x-axis with a protractor.
- Calculate the tangent of this angle, which directly gives you the slope: m = tan(θ).
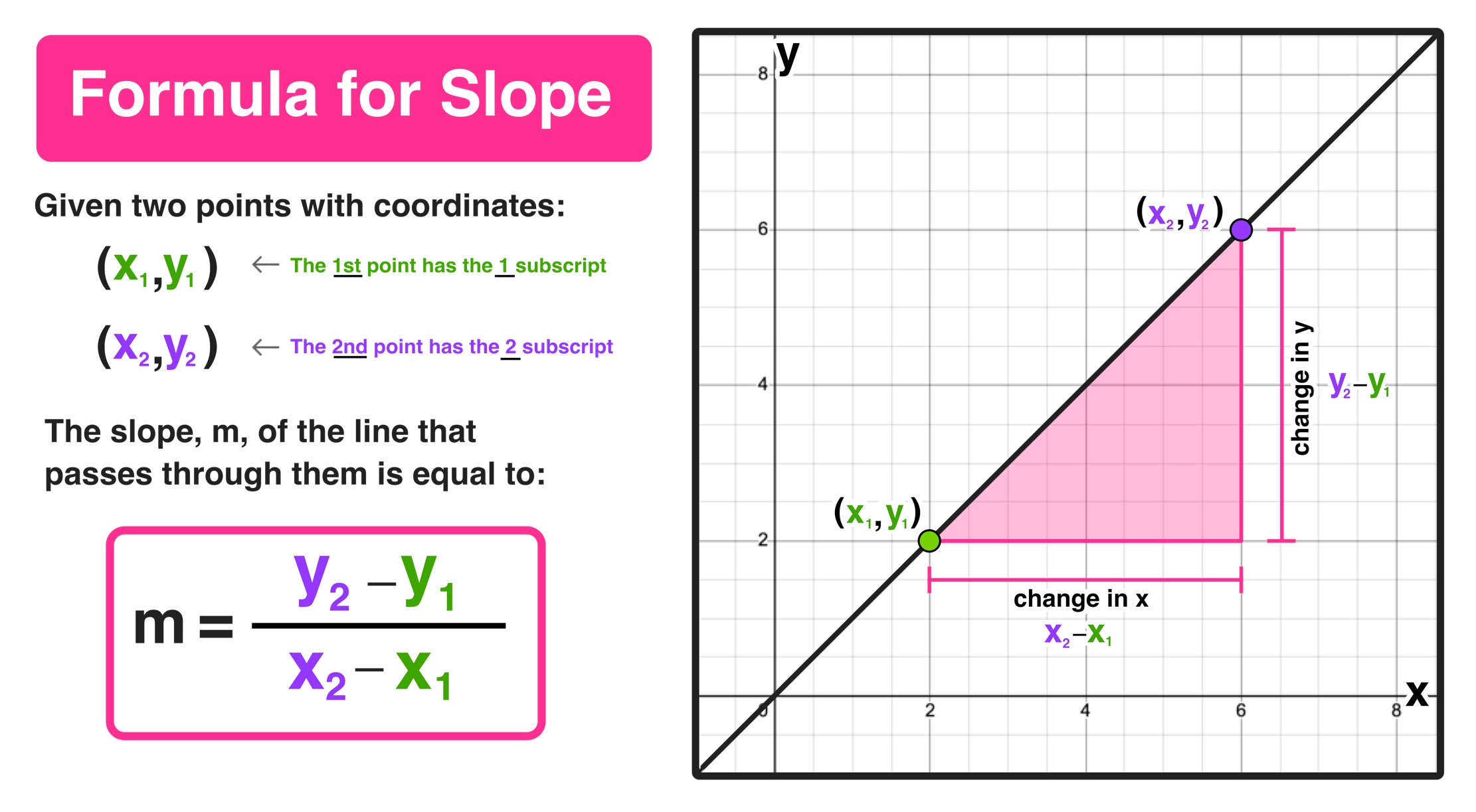
3. Applying the Slope Formula Directly

The mathematical representation for slope, given two points (x1, y1) and (x2, y2), is:
m = (y2 - y1) / (x2 - x1)
- Choose two points on the line.
- Substitute these values into the formula.
- Compute the slope.
4. Using a Slope Calculator
While not the traditional method of manual calculation, online tools can be incredibly useful:
- Enter the coordinates of any two points on the line into an online slope calculator.
- The calculator will instantly compute the slope for you.
💡 Note: Slope calculators are beneficial for quick checks or when dealing with large numbers.
5. Slope-Intercept Form

If you can recognize or derive the equation of the line in slope-intercept form, y = mx + b, the slope is the coefficient ’m’:
- Identify the y-intercept (b) where the line crosses the y-axis.
- Use the coordinates of any point on the line to solve for m in the equation.
The journey of finding the slope of a line from its graph is fundamental in understanding how lines behave in different contexts, from finance to physics. Whether you are an engineer designing a ramp, a physicist analyzing motion, or a student tackling algebra, knowing how to derive slope from a graph can be immensely practical. Each method provides a different perspective on what slope represents, from the physical interpretation of incline to the abstract mathematical approach through equations.
Why is slope important in real life?
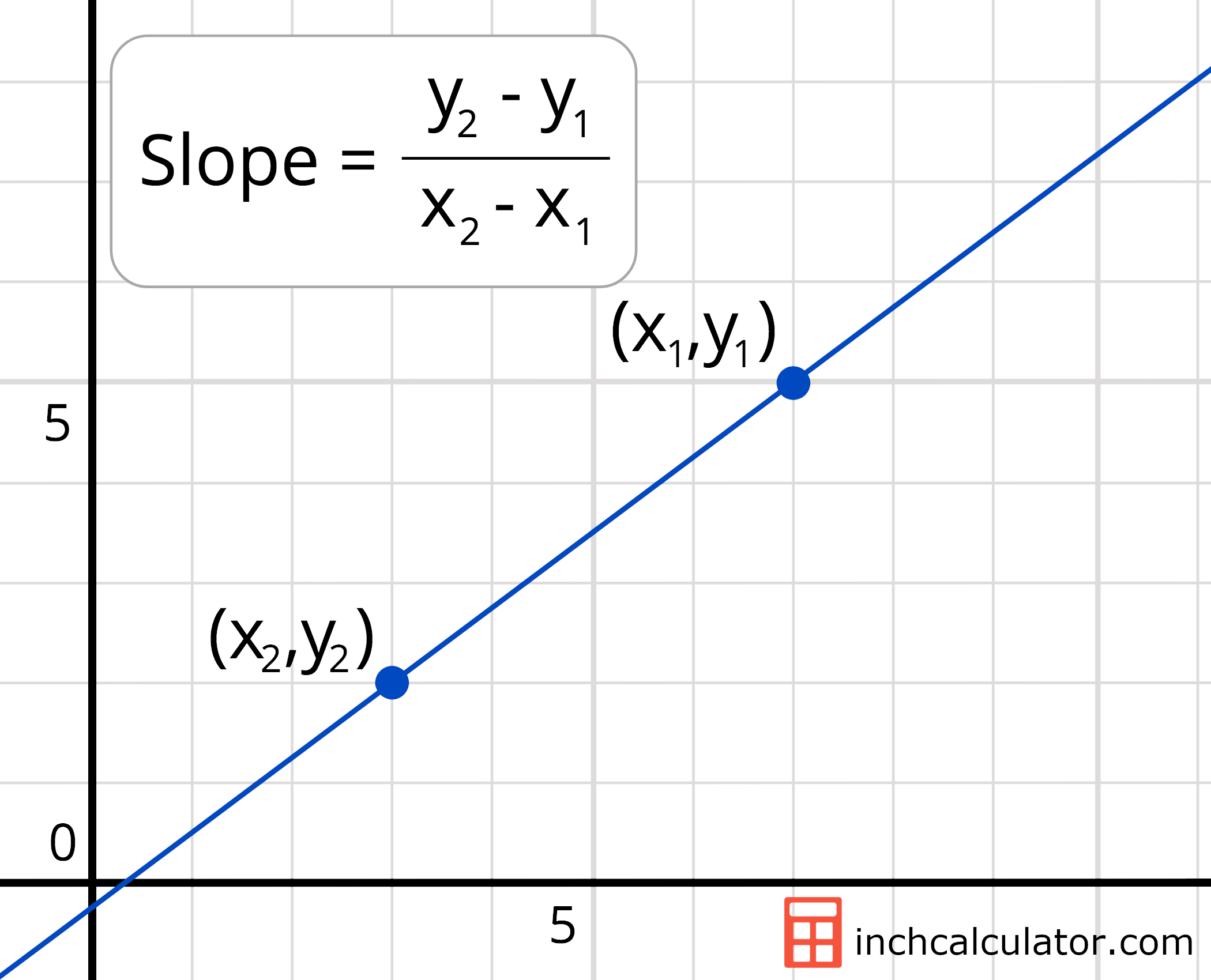
+
Slope is crucial in various fields. For instance, in construction, it determines the pitch of roofs or ramps, ensuring safety and functionality. In finance, it represents growth rates or returns over time. In physics, it’s used to calculate velocity or acceleration when graphing motion.
Can I find the slope if I only have one point on the line?
+
No, to find the slope, you need at least two points. However, if you know one point and the y-intercept, you can derive the equation of the line and find the slope.
What does a negative slope signify?

+
A negative slope signifies that as the x-value increases, the y-value decreases. This typically indicates a line that’s descending from left to right, or a downward trend in data representation.
How do you interpret a slope of 0?
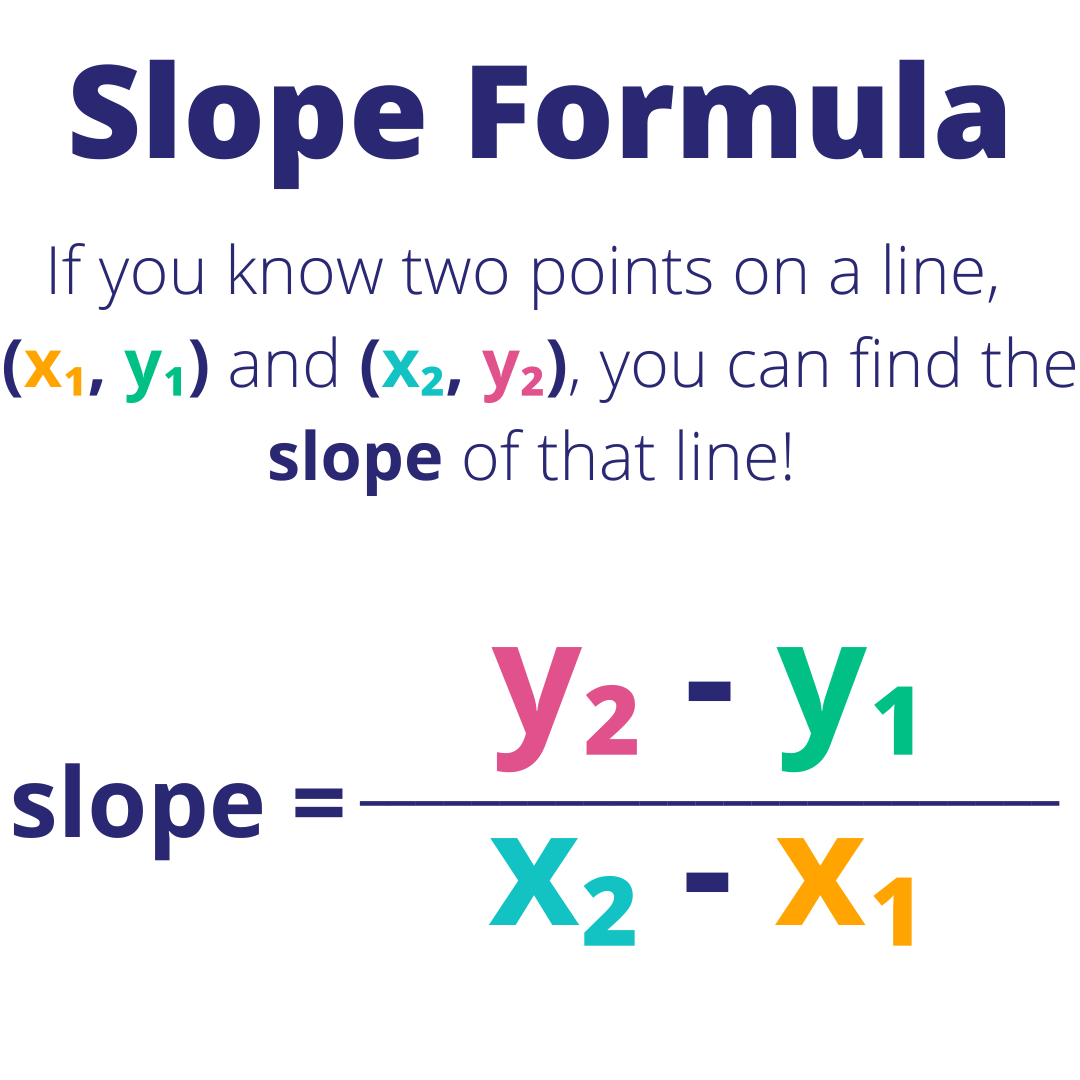
+
A slope of zero means that there is no change in y as x increases. This results in a horizontal line, indicating that the variable being measured remains constant over time or change in x.


