Master the Missing Angles in Triangle Worksheet!
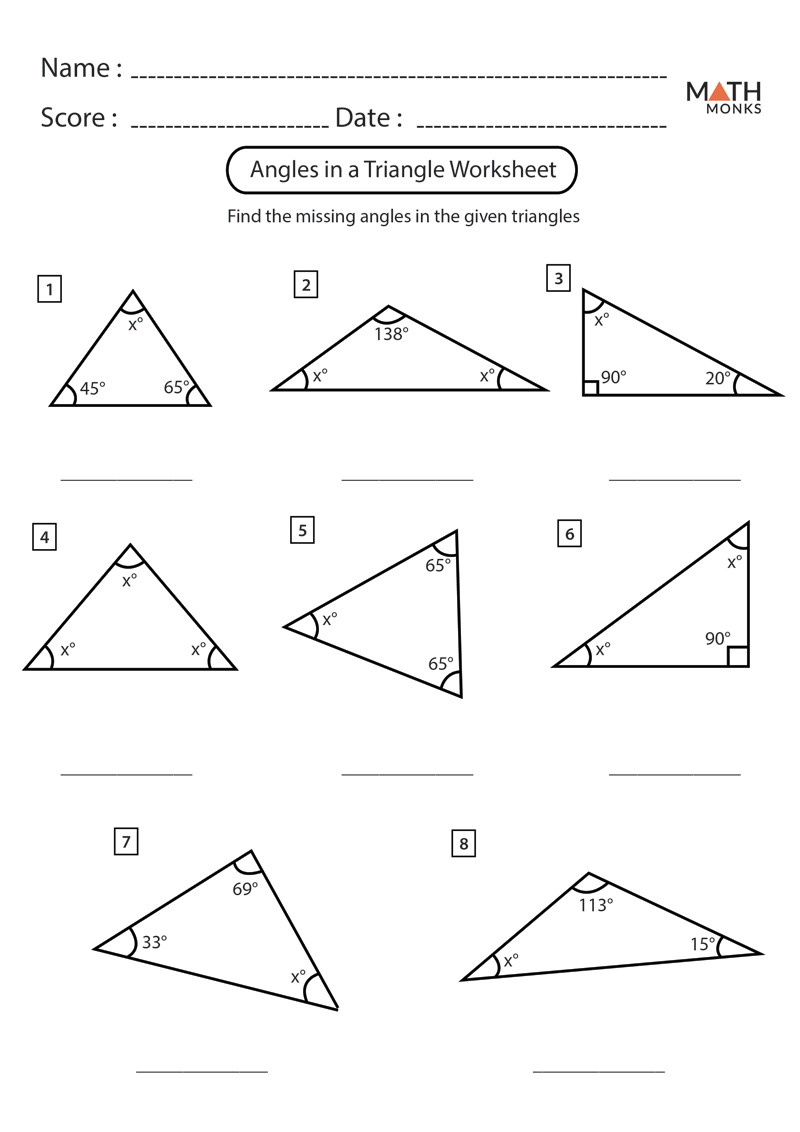
In this comprehensive guide, we'll explore the fascinating world of triangles, focusing on how to solve for missing angles in triangles using a worksheet. Triangles are one of the fundamental shapes in geometry, and understanding how to calculate their angles is crucial for both academic and practical purposes. Whether you're a student looking to master this topic for your exams or an enthusiast exploring the intricacies of shapes, this article will provide you with the knowledge to confidently tackle any triangle angle problem.
The Basics of Triangles
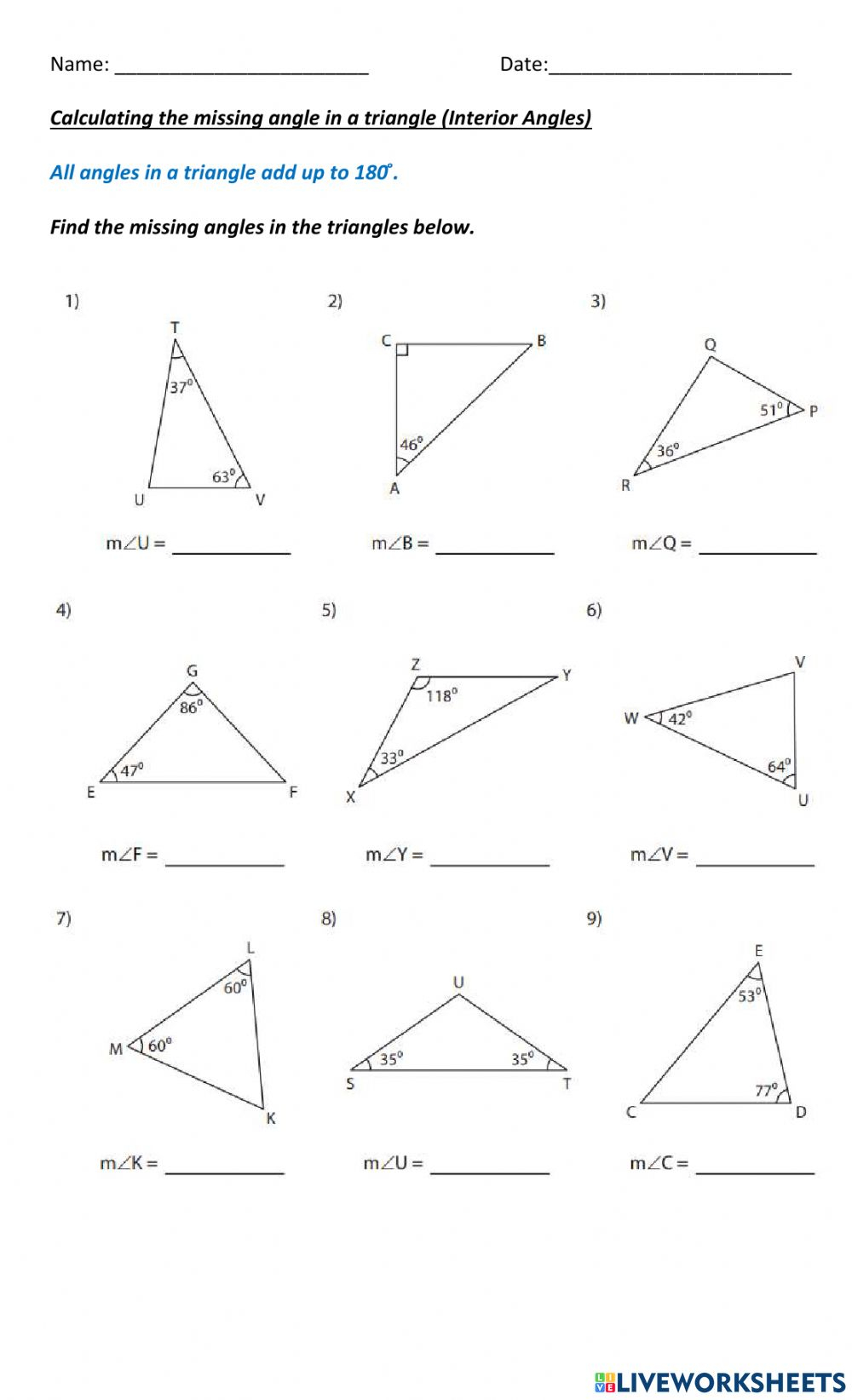
Before diving into solving for missing angles, let's understand the basics:
- Types of Triangles: There are several types of triangles based on their sides and angles:
- Equilateral: All sides and angles are equal (60°).
- Isosceles: Two sides and angles are equal.
- Scalene: All sides and angles are different.
- Right: One angle is 90°.
- Obtuse: One angle is greater than 90° but less than 180°.
- Acute: All angles are less than 90°.
- Sum of Angles in a Triangle: The sum of the internal angles in any triangle is always 180°.
- Exterior Angles: The exterior angle of a triangle is equal to the sum of the opposite interior angles.
Why Angles in Triangles Matter

Understanding the angles of triangles is not just for geometry class; it has real-world applications:
- Architecture and Engineering: To ensure stability and balance in structures, understanding angles is essential.
- Navigation and Surveying: Triangulation methods use angles to determine distances and map locations.
- Astronomy: Calculations involving stars' positions often rely on triangles and their angles.
Approaching Missing Angles
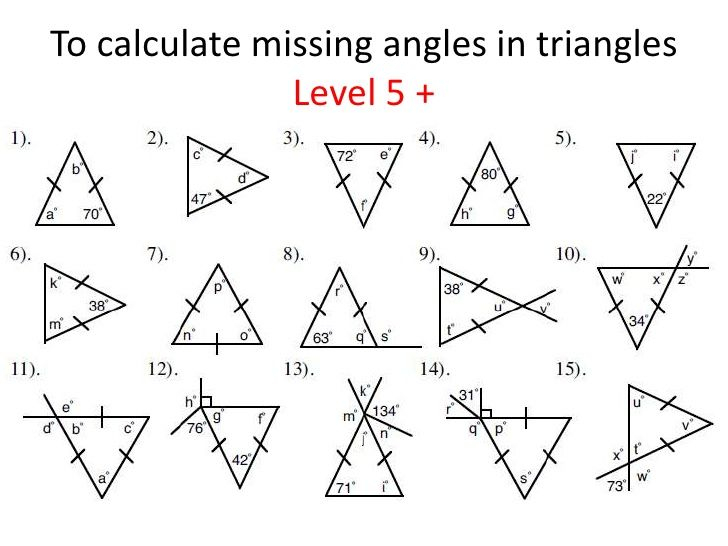
To solve for missing angles in a triangle, you can follow these steps:
- Identify the known angles.
- Use the Triangle Sum Theorem (sum of interior angles equals 180°).
- If applicable, use properties of specific triangle types (e.g., isosceles).
The Triangle Worksheet: A Step-by-Step Guide


Let's delve into a typical missing angles in triangles worksheet to see how to apply these principles:
- Problem 1: In a triangle, two angles are 50° and 70°. Find the third angle.
📝 Note: This is a straightforward example using the Triangle Sum Theorem.
Solution: 1. Sum of angles in a triangle = 180°. 2. Known angles = 50° + 70° = 120°. 3. Missing angle = 180° - 120° = 60°.
- Problem 2: In an isosceles triangle, one angle is 40°. Find the other angles.
📝 Note: Use the properties of an isosceles triangle.
Solution: 1. Two angles are equal in an isosceles triangle. 2. Let the equal angles be x. 3. x + x + 40° = 180° 4. 2x = 140° 5. x = 70° So, the other two angles are 70° each.
Advanced Techniques for Solving Triangle Angles

When dealing with complex triangles, additional geometric laws might be necessary:
- Law of Sines: For non-right triangles, this law relates the sides of a triangle to the sines of its angles.
- Law of Cosines: Useful for finding angles or sides when two sides and an angle or three sides are known.
- Exterior Angle Theorem: The exterior angle of a triangle is equal to the sum of the opposite interior angles.
Common Pitfalls and How to Avoid Them

Here are some common errors to watch out for:
- Miscalculation of the sum of angles (remember it’s 180°, not 360°).
- Forgetting to account for the angle opposite the longest side in obtuse triangles.
- Not recognizing triangle types, which can simplify the solving process.
- Using the wrong formula for the wrong type of problem.
In this extensive exploration of triangle angles, we’ve covered the basics of triangles, their real-world significance, how to approach missing angles, and worked through some problems from a worksheet. The ability to master these calculations not only ensures success in math and geometry courses but also enhances your understanding of spatial relationships. The principles learned here are not only foundational for geometry but are also crucial for understanding more advanced concepts in mathematics and engineering.
The journey to mastering angles in triangles is about more than just solving equations. It’s about developing a keen eye for patterns, understanding how shapes interact, and leveraging these insights to solve problems both on paper and in the physical world.
To solidify your understanding, try to find more examples or worksheets online or create your own scenarios where you calculate missing angles. Engaging with different problem sets will deepen your skills and make you proficient in solving triangle puzzles.
What is the sum of angles in any triangle?

+
The sum of the interior angles of any triangle is always 180°.
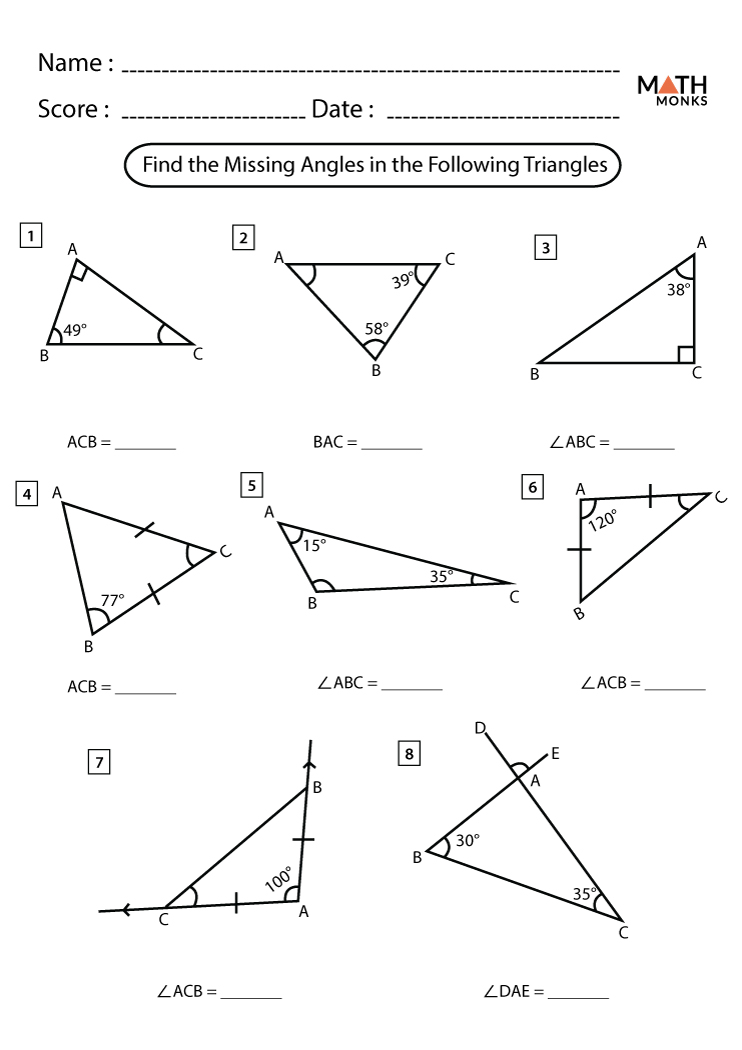
How do you find the missing angle in a triangle?
+
To find the missing angle in a triangle, subtract the sum of the known angles from 180°.
What are some advanced techniques for solving triangles?

+
Advanced techniques include using the Law of Sines for non-right triangles, the Law of Cosines when you have two sides and the included angle, or three sides, and understanding the Exterior Angle Theorem for complex problems involving exterior angles.