5 Simple Steps to Master Algebra Factorization

Algebra factorization is a fundamental skill that opens the door to more advanced mathematics and problem-solving techniques. It involves expressing a polynomial as a product of simpler expressions, making calculations and understanding complex equations much easier. Whether you are a student struggling to grasp the basics or someone keen on refreshing their algebra skills, mastering factorization is critical. Here, we will explore five simple steps to help you master this important mathematical technique.
Understanding the Concept of Factorization

Before diving into the methods, let’s clarify what factorization entails:
- Factorization is the process of breaking down an expression into its multiplicative factors.
- The goal is to simplify complex expressions and to solve equations more efficiently.
Let’s consider the polynomial x^2 + 5x + 6. Here, it can be factored into (x + 3)(x + 2), which is much easier to work with than the original expression.
Step 1: Identify the Common Factors

The first step in factorization is to find if there are any common factors among all the terms of the polynomial. This means:
- Looking for numbers or variables that divide each term.
- Factoring out these common terms.
Example: 2x^2 + 4x. Both terms have 2x as a common factor, so you can factor out 2x:
2x^2 + 4x = 2x(x + 2)
Step 2: Grouping

If common factoring does not work or only simplifies a part of the polynomial, the next step is grouping. Here’s how to do it:
- Group the terms in pairs.
- Factor out the common factor from each group.
- Look for common binomial factors or apply distributive property in reverse.
Example: ax + ay + bx + by. Grouping this, we get:
(ax + ay) + (bx + by) = a(x + y) + b(x + y)
Now, factor out the common binomial (x + y):
(a + b)(x + y)
Step 3: Applying Known Formulas
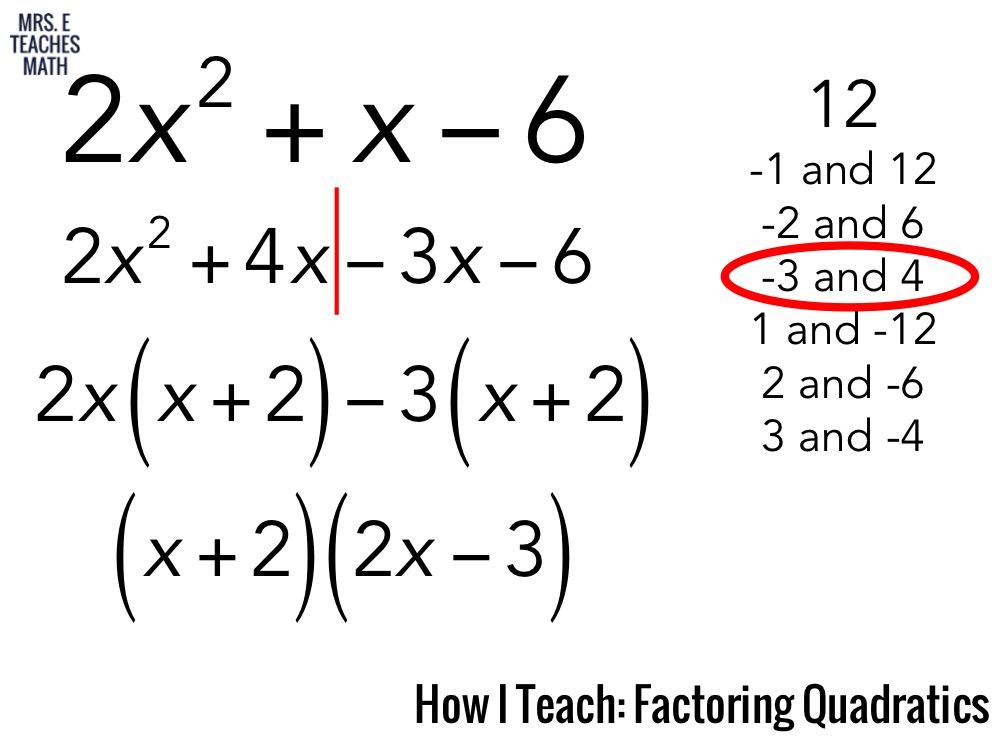
There are several well-known formulas that make factorization easier:
| Formula | Example |
|---|---|
Difference of Squares: a^2 - b^2 = (a - b)(a + b) |
x^2 - 9 = (x - 3)(x + 3) |
Perfect Square Trinomial: a^2 + 2ab + b^2 = (a + b)^2 |
x^2 + 10x + 25 = (x + 5)^2 |
Step 4: Trial and Error

When none of the above methods directly apply, use the trial and error approach:
- Find two numbers whose product equals the constant term and whose sum equals the coefficient of the middle term.
- Express the polynomial as the product of binomials.
Example: x^2 + 7x + 12. The constant is 12, and the coefficient of x is 7. The numbers that fit are 3 and 4:
x^2 + 7x + 12 = (x + 3)(x + 4)
Step 5: Factoring Trinomials with Higher Powers

When dealing with trinomials of higher powers (like a^3 + b^3), use the sum or difference of cubes:
- Sum of Cubes:
a^3 + b^3 = (a + b)(a^2 - ab + b^2) - Difference of Cubes:
a^3 - b^3 = (a - b)(a^2 + ab + b^2)
Example: 8x^3 - 27:
8x^3 - 27 = (2x)^3 - 3^3 = (2x - 3)((2x)^2 + (2x)(3) + 3^2)
🔖 Note: Always check your factorization by expanding the result to ensure it matches the original polynomial.
Ensuring Proficiency

Mastering these steps requires:
- Practice with various polynomials to become proficient in recognizing which method to apply.
- Patience, as factorization can sometimes require trial and error.
These steps provide a framework for algebra factorization, allowing you to tackle polynomials of various degrees and complexities. Understanding these techniques will not only aid in problem-solving but also enhance your ability to understand and manipulate mathematical expressions effectively.
The journey towards mastering factorization is rewarding and opens up numerous pathways in mathematics. Whether you're solving equations, simplifying algebraic expressions, or preparing for higher-level math courses, these steps form a solid foundation. Keep practicing, and soon, you'll find yourself tackling even the most challenging factorization problems with confidence.
What if my polynomial can’t be factored using these steps?

+
Some polynomials are not factorable over the integers. These are known as irreducible polynomials.
How can I make factorization faster?

+
Practice is key. Additionally, recognizing common factorable forms quickly can speed up the process.
Can factorization help with real-world problems?

+
Yes, factorization is used in areas like coding, cryptography, engineering, and even financial modeling to simplify complex formulas.



