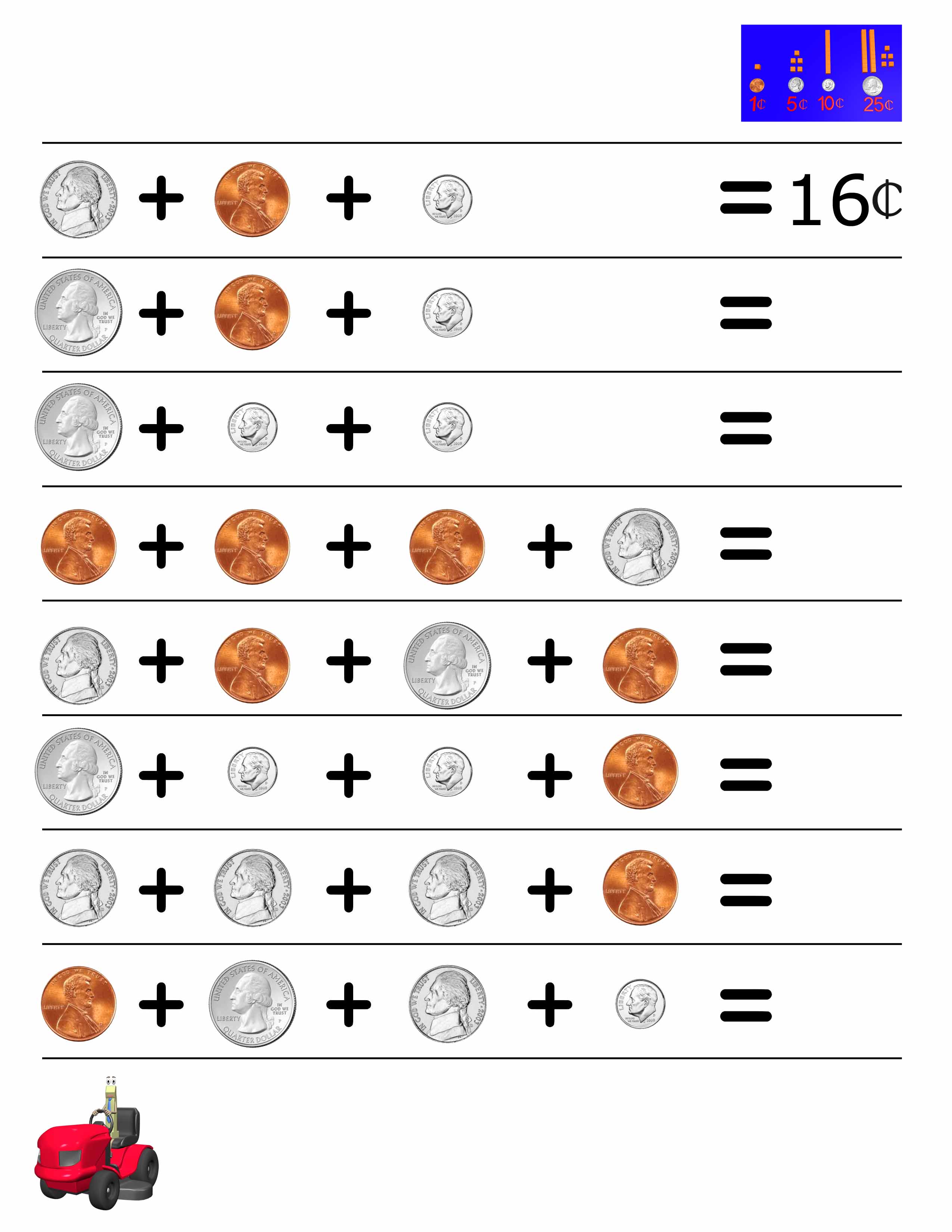
5 Quick Tips for GCF Factoring Worksheet Answers

In mathematics, finding the Greatest Common Factor (GCF) is fundamental for simplifying expressions, solving equations, and factoring polynomials. Whether you are a student learning these skills for the first time or a seasoned teacher looking for new ways to explain GCF factoring, these quick tips will help you navigate GCF factoring worksheet answers with ease and precision.
Understanding the Concept of GCF

The GCF, or greatest common factor, is the largest number or term that divides evenly into two or more numbers or terms without leaving a remainder. Before diving into the worksheet, it’s crucial to ensure you or your students have a firm grasp of this concept:
- Prime factorization: Break down numbers into their prime factors. For example, the GCF of 12 and 18 is found by seeing that they share the factors 2 and 3, thus the GCF is 6.
- Identify common factors: After factoring, look for common factors in the list.
Visualizing Factors with a Number Tree
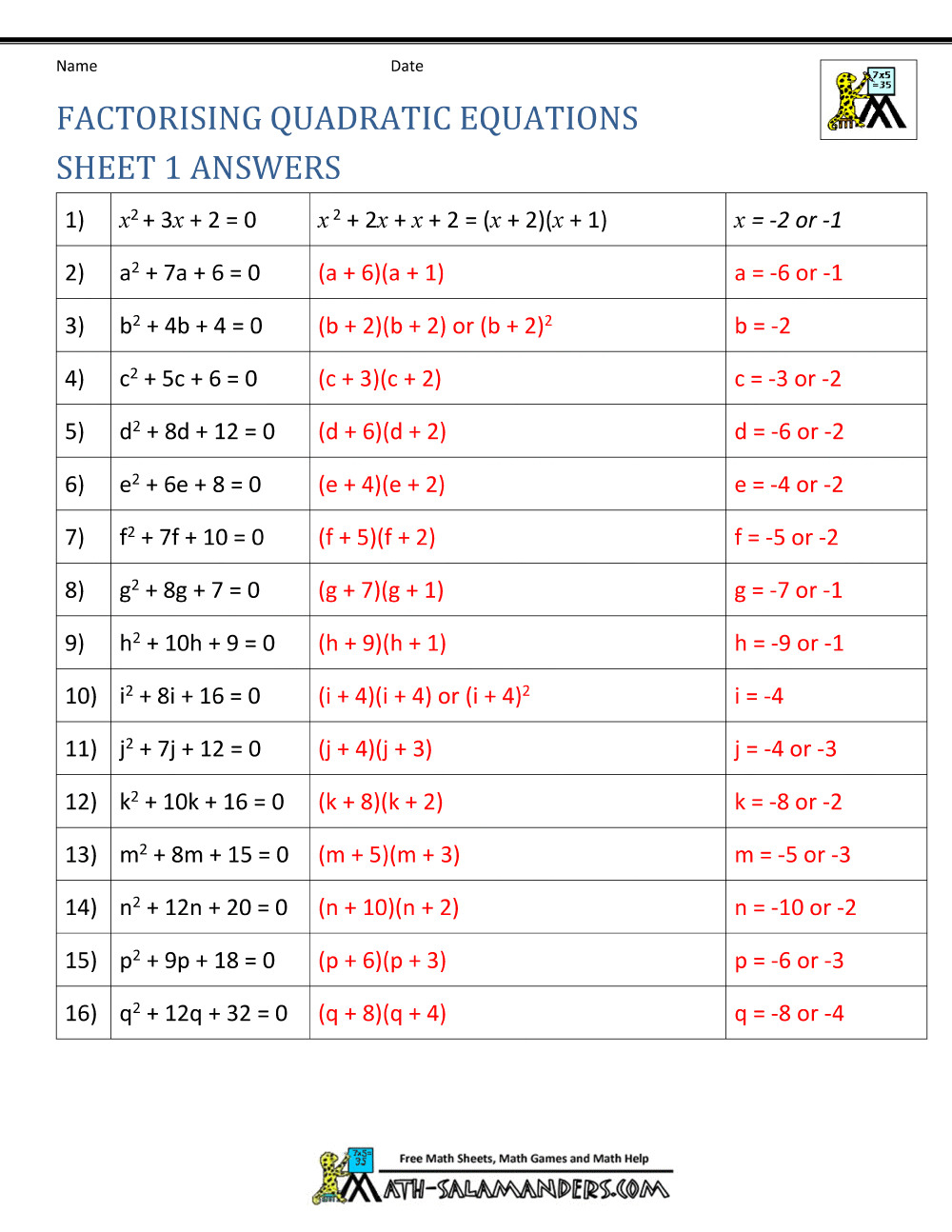
To make the process more visual:
- Create a tree diagram showing the prime factors of each number or term.
- Use colors to distinguish between common and non-common factors. Common factors can be highlighted in one color, making the GCF visually obvious.
- Label each branch with its prime factors, helping to identify shared numbers or terms.
Simplify the Problem

Sometimes, problems on GCF worksheets can be overly complicated:
- Use smaller numbers: If dealing with large numbers, reduce them by dividing by a common factor before finding the GCF.
- Polynomials: Simplify each polynomial term by factoring out common terms first.
Create a GCF Cheat Sheet
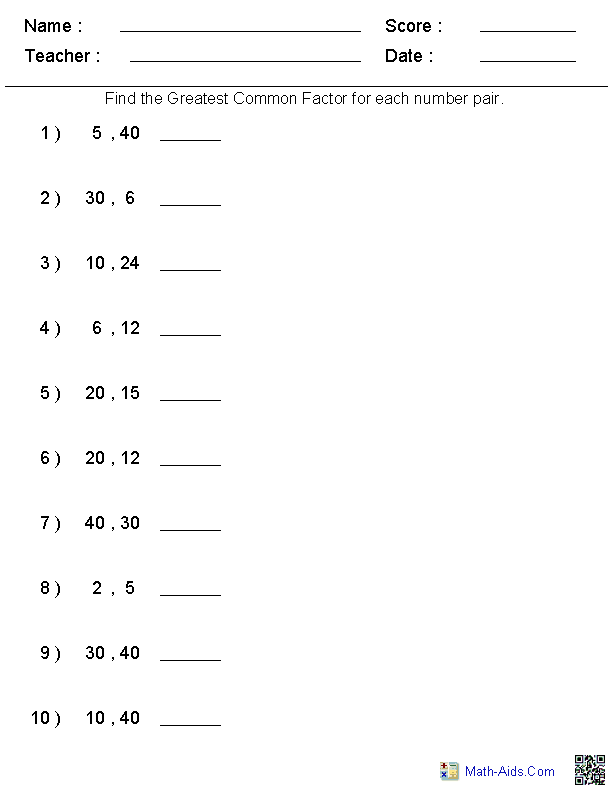
A handy reference can be a lifesaver:
- List the prime numbers up to 20 or 30.
- Develop a table for common GCFs for numbers up to 100 or specific common denominators.
| Number 1 | Number 2 | GCF |
|---|---|---|
| 18 | 24 | 6 |
| 35 | 45 | 5 |

Practice with Varied Examples

Engaging with various types of problems helps reinforce the concept:
- Include different scenarios where GCF needs to be applied, such as simplifying fractions, factoring polynomials, and solving word problems.
- Encourage students to solve the same problem in different ways to deepen understanding.
🌟 Note: While GCF is fundamental for simplifying, remember to teach students how to apply this knowledge beyond worksheets.
From understanding the basics to advanced applications, GCF factoring is not just about finding the largest common factor but about developing a thought process that simplifies complex mathematics. Students equipped with these quick tips will find GCF worksheets more approachable, enhancing their mathematical proficiency.
Why is GCF important in factoring?

+
Finding the GCF allows for the simplification of algebraic expressions and equations, making problem-solving more manageable.
Can I use these tips for factoring polynomials as well?

+
Yes, these tips, especially those on visual aids and simplification, can be adapted to factoring polynomials.
How can I make GCF factoring more fun for students?

+
Games, puzzles, and incorporating real-world examples where GCF solving is necessary can make the learning process more engaging.