8th Grade Exponents Mastery: Free Worksheets
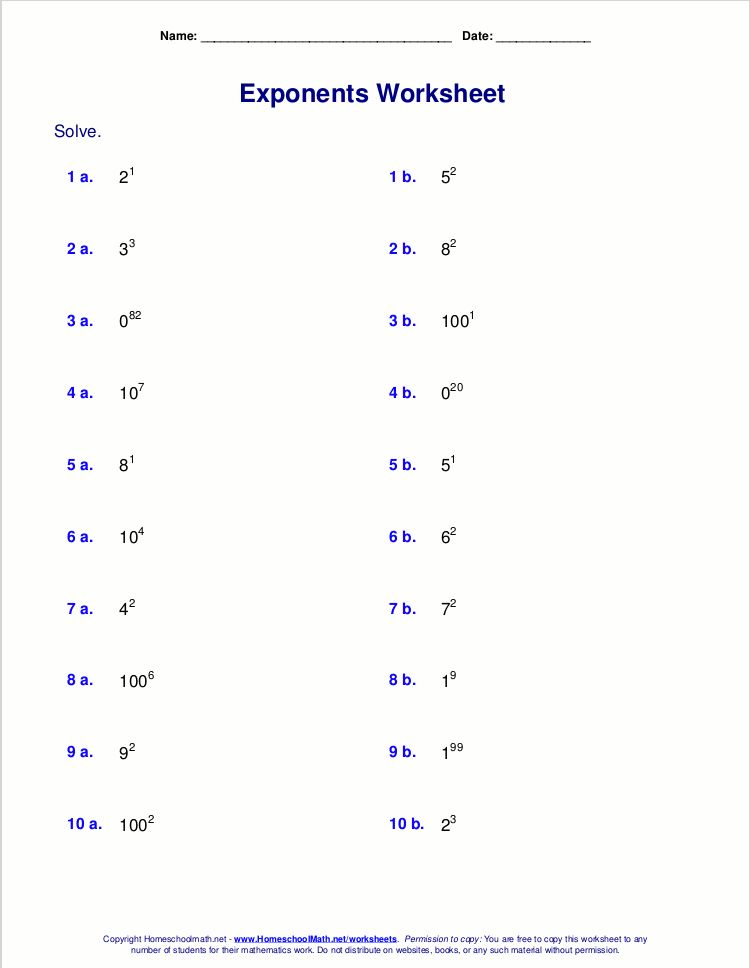
The mastery of exponents is a pivotal part of an 8th grader's journey in mathematics. Exponents, often introduced in middle school, lay the groundwork for algebraic concepts like exponential functions and logarithms that students will encounter in higher grades. Understanding exponents not only simplifies mathematical calculations but also makes many equations more manageable. In this blog post, we will dive deep into how to master exponents, providing free worksheets for practice to help 8th graders enhance their skills effectively.
The Basics of Exponents
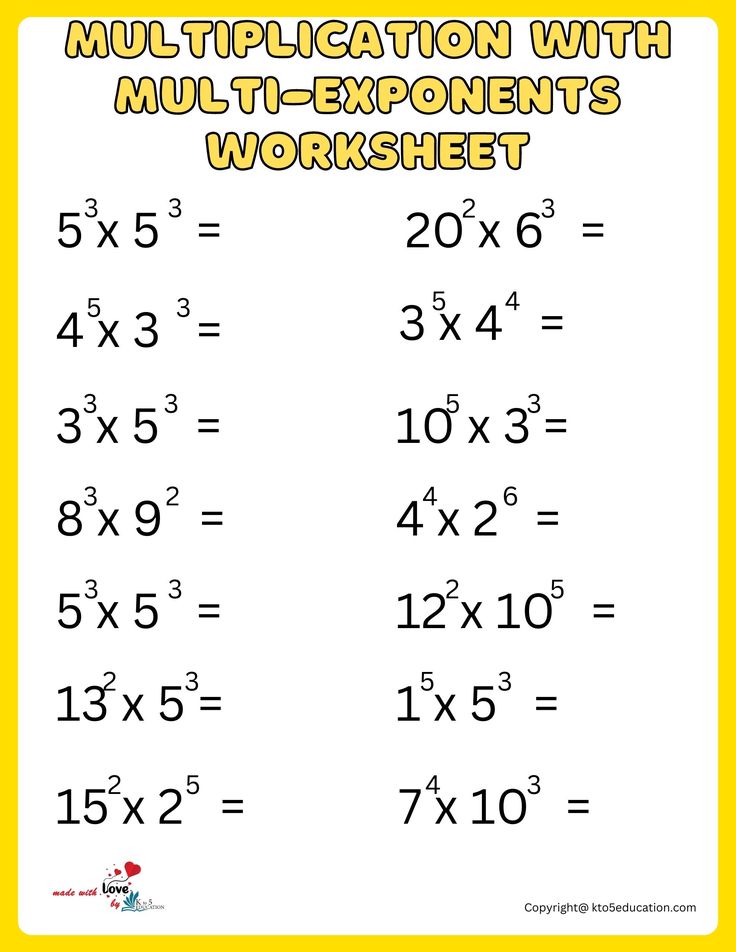
Exponents are a shorthand way of expressing repeated multiplication of the same number:
- a^n where a is the base and n is the exponent. Here are some basic rules:
- a^m * a^n = a^(m+n) - When multiplying numbers with the same base, add the exponents.
- a^m / a^n = a^(m-n) - When dividing, subtract the exponents.
- (a^m)^n = a^(m*n) - To raise a power to a power, multiply the exponents.
- a^0 = 1 - Any nonzero number raised to the power of 0 is 1.
- a^1 = a - Any number raised to the power of 1 is itself.
- (ab)^n = a^n * b^n - When a product is raised to an exponent, raise each factor to that power.
💡 Note: Remember that exponents can also be negative or fractional, but for 8th graders, the focus is usually on positive integer exponents.
Worksheets to Enhance Exponents Skills

To become proficient in exponents, practice is essential. Here are some worksheet activities designed to improve understanding:
- Basic Exponent Rules: Worksheets where students need to combine exponents using the rules above.
- Simplifying Expressions: Practice sheets for simplifying expressions with multiple exponents.
- Applying Exponents in Problems: Problems where students must use exponents to solve real-life scenarios, like compound interest calculations.
| Worksheet Type | Description |
|---|---|
| Rule Application | Students apply basic exponent rules to combine or simplify expressions. |
| Simplification | Tasks involve simplifying exponential expressions with multiple operations. |
| Problem Solving | Application of exponents in real-world problems, enhancing conceptual understanding. |

Strategies for Learning Exponents
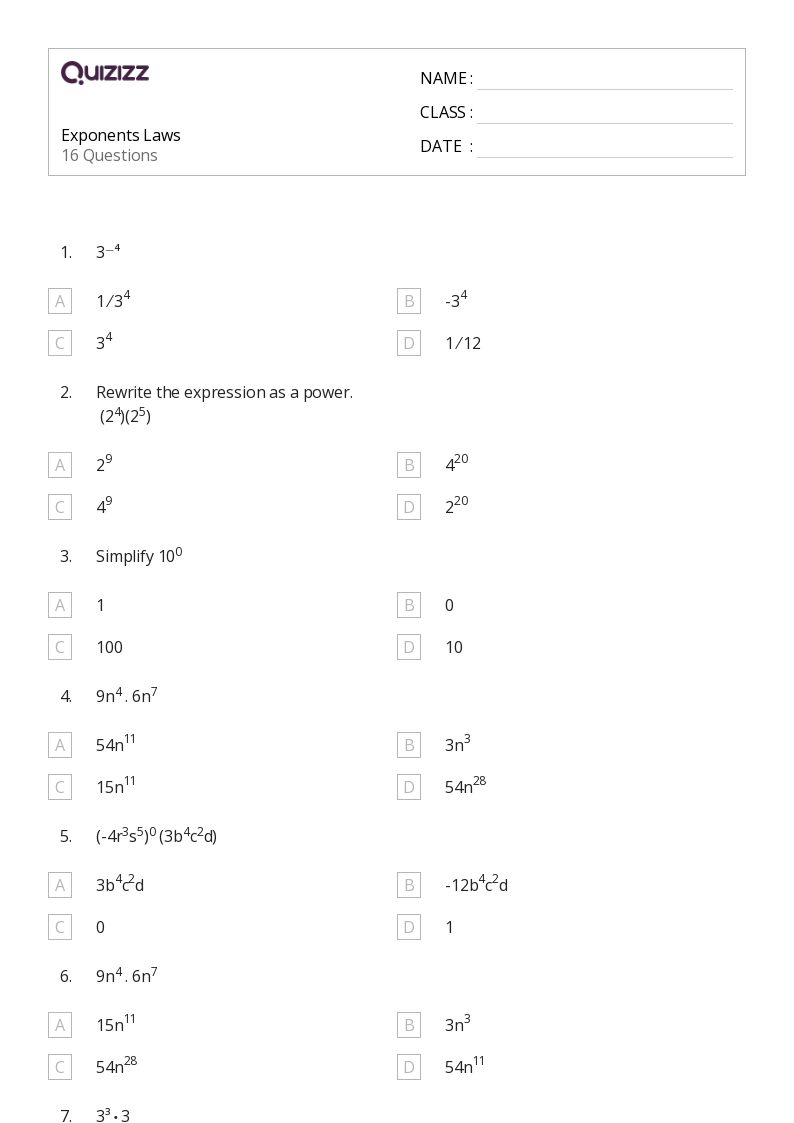
Learning exponents can be approached in several effective ways:
- Visualization: Use diagrams or tools like exponential towers to visualize how exponents work.
- Practice: Regularly work on problems to internalize the rules.
- Understanding the Base: Ensure students understand what a base means before moving to exponents.
- Using Technology: Graphing calculators or educational apps can help visualize and solve exponential problems.
Integrating Exponents into Other Subjects

Exponents are not just mathematical tools; they have applications across various subjects:
- Science: Exponential growth or decay, like in population dynamics or radioactive decay.
- Finance: Compound interest calculations.
- Computer Science: Big O notation for algorithm analysis.
Integrating these into lessons can make exponents more relevant and interesting.
🔎 Note: Linking exponents to real-world applications can boost student interest and retention.
Common Mistakes and How to Avoid Them

Here are some common pitfalls in understanding exponents and how to avoid them:
- Multiplying Exponents Instead of Adding: Remember to add exponents when multiplying the same base, not multiply them.
- Confusing Negative Exponents: A negative exponent means the reciprocal of the positive exponent. Educate on this relationship.
- Order of Operations: Exponents must be calculated before addition and subtraction.
In wrapping up, mastering exponents for 8th graders is more than just learning rules; it's about understanding the power of numbers, their patterns, and how they grow. Practice with carefully crafted worksheets, along with exploring real-life applications, not only solidifies this understanding but also enriches the learning experience. Exponents are foundational for higher math, science, and even finance, making their mastery an essential skill for young learners to carry into their future studies.
What are the basic exponent rules?

+
The basic rules of exponents include: a^m * a^n = a^(m+n), a^m / a^n = a^(m-n), (a^m)^n = a^(m*n), a^0 = 1, a^1 = a, and (ab)^n = a^n * b^n.
How do I explain exponents to my child?

+
Start by explaining that exponents are shorthand for repeated multiplication of the same number. Use simple examples like 2^3 = 2 * 2 * 2, and relate it to real-life scenarios like growing bacteria or calculating interest rates to make it more engaging.
Why is practice with worksheets important for learning exponents?

+
Worksheets allow students to practice repeatedly, reinforcing the rules and methods of exponent manipulation. This repetitive practice helps in internalizing concepts, improving speed, and reducing errors in mathematical operations involving exponents.
Can you provide examples of real-life applications of exponents?

+
Exponents are used in population growth models, financial calculations like compound interest, in understanding radioactive decay, and even in computer science for algorithm analysis (Big O notation).