5 Essential Tips for Mastering Exponent Worksheet Answers

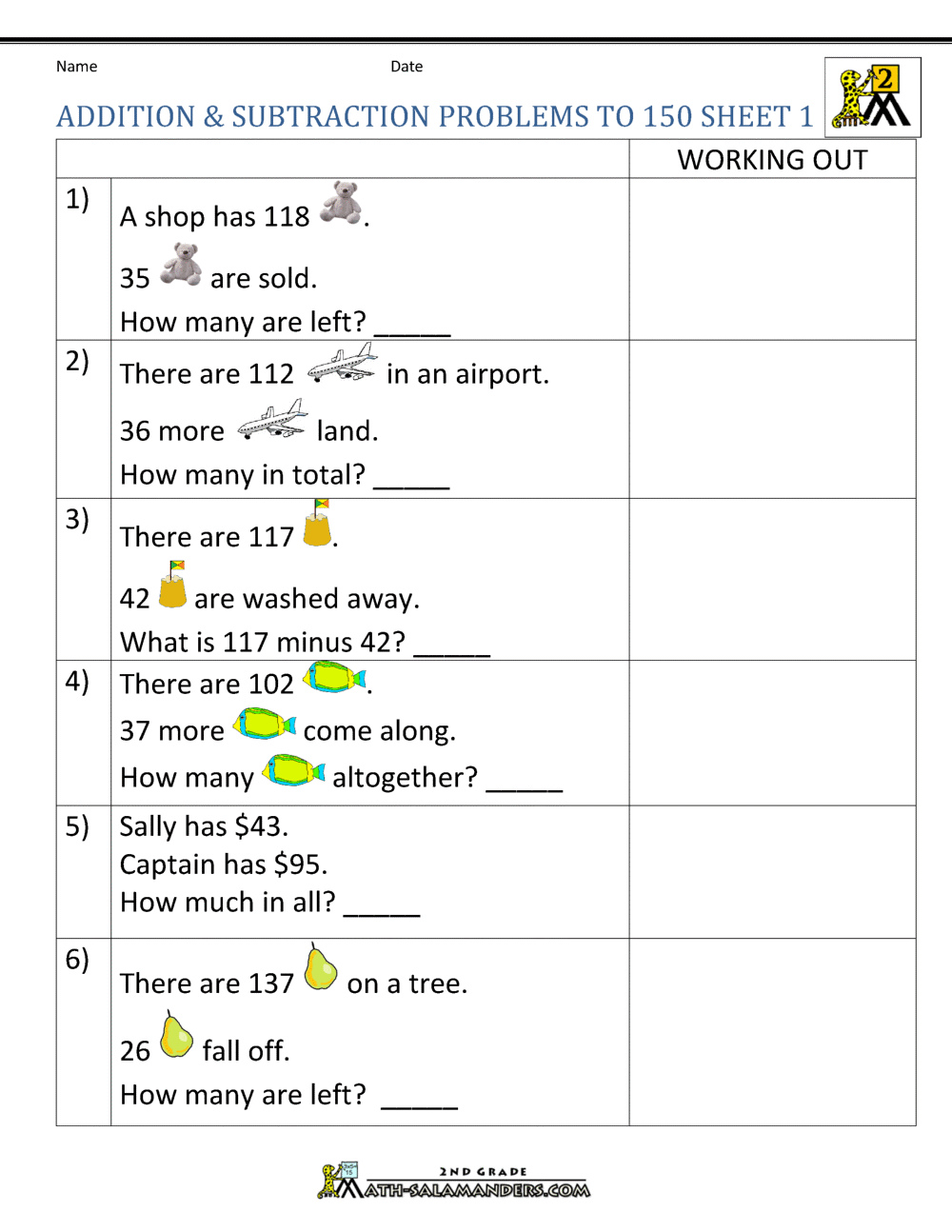
Mathematics, particularly the field of algebra, can be quite daunting for many students. One of the fundamental aspects of algebra is exponents, which often pose a unique challenge due to their abstract nature. This complexity increases when students are tasked with solving exponent worksheet answers. Whether you're a high school student striving to excel in algebra or an adult returning to studies, mastering exponent worksheet answers is crucial for mathematical proficiency. Here are five essential tips to help you conquer this mathematical beast and become adept at handling exponent problems.
Tip #1: Understand the Basics of Exponents

Before diving into complex exponent problems, it’s imperative to have a firm grasp of what exponents are and how they work. Here are some key points:
- Exponent Definition: An exponent denotes the number of times a number (the base) is multiplied by itself.
- Multiplication and Division: When multiplying or dividing powers with the same base, you add or subtract the exponents respectively. For example: (a^m \times a^n = a^{m+n}), and (a^m / a^n = a^{m-n}).
- Power to a Power: If an exponent is raised to another exponent, multiply the exponents. For instance, ((a^m)^n = a^{m*n}).
- Zero Exponents: Any non-zero number to the zero power is 1. For example, (5^0 = 1).

⚠️ Note: Remember that an exponent of 1 doesn't change the base value, e.g., x^1 = x.
Tip #2: Master the Properties of Exponents

Understanding exponent properties can significantly simplify calculations. Here’s a breakdown:
- Product of Powers: (a^m \cdot a^n = a^{m+n})
- Quotient of Powers: (a^m / a^n = a^{m-n})
- Power to a Power: ((a^m)^n = a^{m*n})
- Distributive Property: ((ab)^m = a^m \cdot b^m)
- Negative Exponents: (a^{-m} = \frac{1}{a^m})
| Property | Example | Result |
|---|---|---|
| Product of Powers | 2^3 \cdot 2^2 | 2^5 = 32 |
| Quotient of Powers | 5^6 / 5^3 | 5^3 = 125 |
| Power to a Power | (3^2)^4 | 3^8 = 6561 |


Tip #3: Practice Simplifying Exponent Expressions
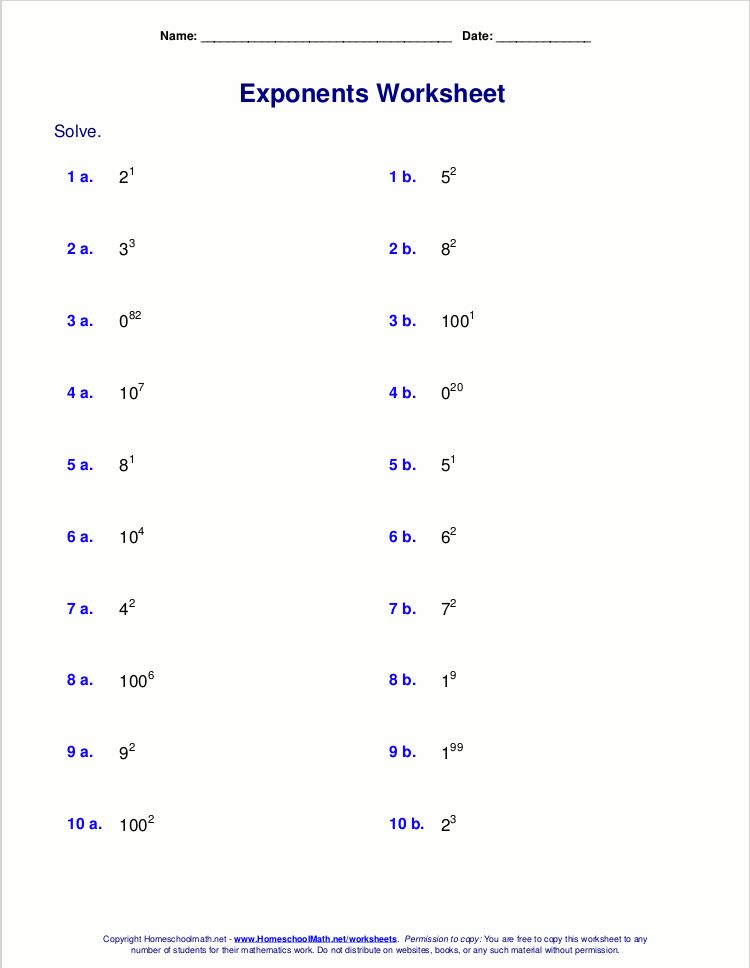
Simplifying expressions involving exponents is an exercise that requires practice. Here’s how to approach it:
- Step-by-Step: Simplify expressions one property at a time.
- Combine Like Terms: If possible, combine like terms before applying exponent rules.
- Reverse Operations: Often, exponent expressions can be manipulated by working backward to simplify.
Let’s take an example: Simplify ( (2^3 \times 2^2) / 2^4 ):
- Apply the product of powers: (2^{3+2} / 2^4 = 2^5 / 2^4)
- Apply the quotient of powers: (2^{5-4} = 2^1 = 2)
🎯 Note: Regular practice in simplifying expressions will not only improve your speed but also your understanding of how exponents interact.
Tip #4: Use Visual Aids and Diagrams

Visual aids can be incredibly useful in mastering exponent worksheet answers:
- Exponent Trees: Use trees to break down exponents, showing each multiplication.
- Number Line: Representing exponential growth or decay visually can help in understanding large or fractional exponents.
- Flowcharts: Visualize the order of operations when simplifying complex expressions.

Tip #5: Review and Learn from Mistakes

Learning from mistakes is fundamental for growth in any skill:
- Track Mistakes: Keep a record of the types of mistakes you make and why they happened.
- Worksheet Analysis: Analyze worksheets with incorrect answers, understand the concepts or steps missed.
- Seek Help: Don’t hesitate to ask for clarification or guidance from teachers or classmates.
🚨 Note: Often, mistakes are repeated because we rush through problems. Take your time to understand each step.
In summary, mastering exponent worksheet answers requires a combination of understanding the basics, knowing properties, practicing simplification, using visual aids, and learning from your mistakes. By applying these tips, you will not only become more proficient in handling exponents but also develop a deeper appreciation for their applications in mathematics. As you progress, remember that proficiency comes with consistent practice and a commitment to understanding the underlying principles of mathematics. Keep exploring, practicing, and you'll find exponents becoming less of a mystery and more of a tool you can wield confidently in your mathematical toolkit.
Why are exponents important in mathematics?

+
Exponents are used to represent repeated multiplication, which is fundamental for understanding exponential growth, scientific notation, and various mathematical models. They simplify large numbers and express complex calculations efficiently.
What is the fastest way to calculate large exponents?

+
Using a calculator is the fastest method, but for mental calculation or understanding, you can use exponent properties to break down the problem or apply logarithms to simplify multiplication.
How can I improve my performance on exponent worksheets?

+
Practice regularly, understand the underlying principles, use visual aids to better grasp the concepts, and analyze your mistakes to prevent them from recurring.