5 Essential Tips for Exponents Worksheet Mastery

In the quest for mathematical proficiency, understanding and mastering exponents is fundamental. Exponents, or powers, are shorthand notations for repeated multiplication, significantly reducing the complexity of certain calculations. As students progress through their mathematical journey, from basic arithmetic to more advanced algebra and beyond, the use of exponents becomes increasingly prevalent. However, many students struggle with these concepts, finding them abstract or difficult to grasp. Here are five essential tips to help with exponents worksheet mastery, ensuring that you or your students can confidently tackle any problem involving these mathematical giants.
Understand the Basics

Before diving into complex exponent problems, it's crucial to solidify the basics:
- What is an exponent? An exponent tells you how many times to multiply a base number by itself. For example, 32 means 3 x 3, which equals 9.
- Zero Exponents: Any non-zero number raised to the power of zero is 1.
- Negative Exponents: A negative exponent signifies that you should find the reciprocal of the base raised to the positive exponent. For example, 2-3 means 1 / (23), which equals 1/8.
- Fractional Exponents: These denote taking roots as well as powers. For example, 81/3 means the cube root of 8, which is 2.

💡 Note: Familiarity with these fundamental rules will make subsequent learning and practice much easier.
Master the Properties

The properties of exponents are the backbone of advanced calculations:
- Product Rule: When multiplying numbers with the same base, add the exponents. For example, am x an = am+n.
- Quotient Rule: When dividing numbers with the same base, subtract the exponents. For example, am / an = am-n.
- Power of a Power: To raise a power to another power, multiply the exponents. For instance, (am)n = amn.
- Distributive Property: You can distribute an exponent to each number within parentheses if they are raised to a power, or factorize an exponent if you have a common base. For example, (a x b)n = an x bn.
💡 Note: Knowing when and how to apply these rules can greatly simplify complex exponent expressions.
Practice Regularly

Mathematics, like any other skill, requires consistent practice:
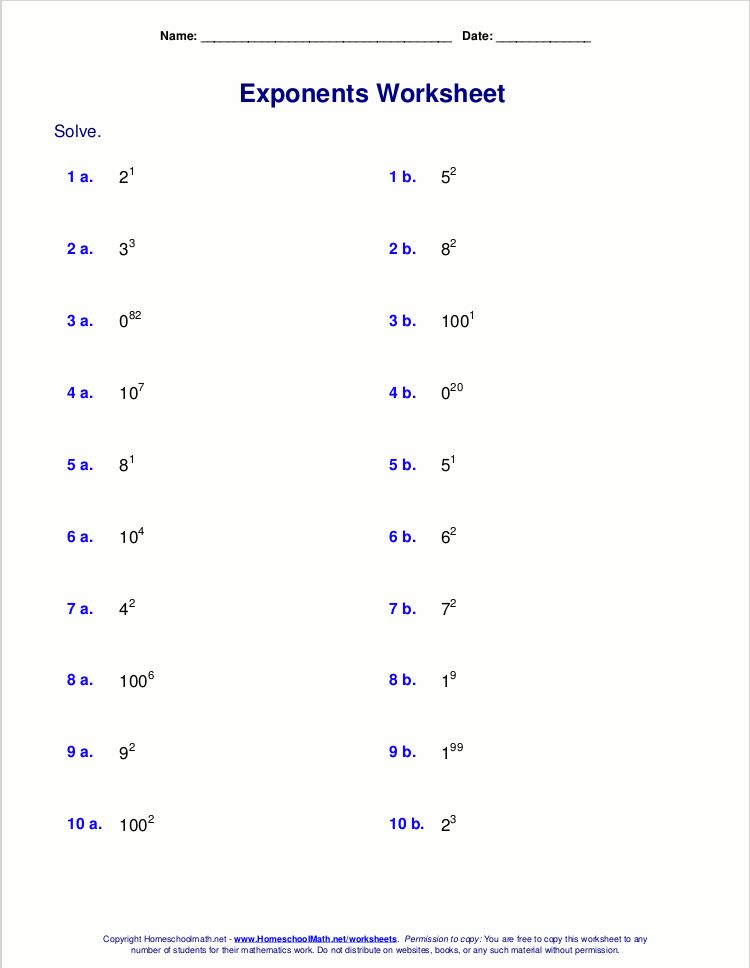
- Worksheets: Utilize exponents worksheets that cover a wide range of difficulty. Start with basic problems and progressively include more complex ones.
- Online Resources: Take advantage of online math practice tools and apps that offer interactive problems and instant feedback.
- Timed Tests: Time yourself to enhance speed and accuracy. It's not just about solving problems; it's about solving them efficiently.
- Real-World Applications: Understand how exponents are used in the real world, like in finance (interest rates), science (exponential decay or growth), or computing (binary systems).

Develop Problem-Solving Strategies

Here are some strategies to approach exponent problems systematically:
- Recognize Patterns: Exponents often follow predictable patterns. For instance, negative exponents involve reciprocals, zero exponents are always 1, and fractional exponents involve roots.
- Write Out Steps: If you're unsure, write down every step to see the problem unfold. This can help in understanding the process and catching mistakes.
- Use Known Theorems: Like De Moivre’s Theorem or Newton’s Binomial Theorem, which can be especially useful for higher-level math involving exponents.
- Substitute Numbers: When dealing with variables, substitute simple numbers to check if your logic is correct.
💡 Note: Developing a methodical approach to problem-solving reduces errors and enhances comprehension.
Connect Concepts with Visuals

Visual aids can help solidify the abstract nature of exponents:
- Exponent Trees: Create tree diagrams to visually represent the growth or repetition of multiplication as exponents increase.
- Number Lines: Plot powers of numbers on a number line to see how quickly they grow.
- Graphs: Use graphs to plot exponential functions and observe their behavior. This helps in understanding not just the concept of exponents but also their applications in real-world scenarios.
| Exponent Concept | Visual Representation |
|---|---|
| Multiplication of Exponents |  |
| Exponential Growth |  |

In summarizing these tips, mastering exponents involves understanding the foundational rules, applying properties, practicing regularly, developing strategic problem-solving skills, and connecting abstract concepts with visual aids. These steps not only help in understanding but also in retaining knowledge about exponents, making them an integral part of a student’s mathematical toolkit. With these strategies in place, anyone can confidently navigate exponents worksheets and apply their knowledge in broader mathematical contexts, making math not just a subject but a useful tool for understanding the world around us.
Why are exponents important?

+
Exponents are essential in mathematics because they simplify the notation for repeated multiplication, which is fundamental for understanding and solving problems involving large numbers, growth rates, and scientific notation.
How do I remember the rules of exponents?
+
Repetition and practice are key. Regularly working with exponents and associating the rules with their application in problems can help in memorization. Creating mnemonics or visual aids can also reinforce your memory.
Can you give a real-world example where understanding exponents is useful?

+
Exponential functions describe phenomena like population growth, radioactive decay, or the growth of investments. For instance, understanding the rule for calculating compound interest involves exponents.