5 Essential Exponent Rules Worksheets for Math Mastery
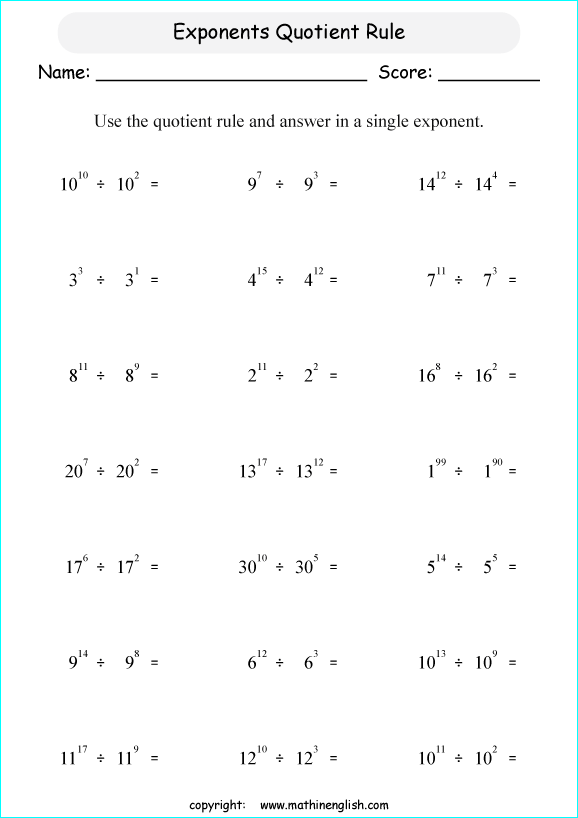
The mathematical journey to understanding and mastering exponents is a crucial step in arithmetic and algebra. Exponent rules, or the laws of exponents, provide a set of guidelines for simplifying expressions involving powers or exponents. These rules help us to work through complex equations with relative ease. This post will explore five essential exponent rules worksheets that are designed to enhance your proficiency in exponents, offering structured practice for various proficiency levels from basic to advanced.
Why Exponent Rules Matter

Exponents are not just about powering up numbers; they are fundamental in simplifying expressions, solving equations, and understanding growth rates in fields like economics, physics, and engineering. Here’s why mastering exponent rules is essential:
- Simplicity: They reduce complex mathematical operations to manageable calculations.
- Efficiency: You can solve problems much faster once you understand these rules.
- Deep Understanding: Exponents offer insights into how numbers interact with each other in multiplicative ways.
The Five Essential Exponent Rules Worksheets

1. The Product Rule Worksheet


The first worksheet focuses on the Product Rule, which states that when multiplying two exponents with the same base, you add their exponents:
am * an = a(m+n)
Here's a structured exercise to practice this rule:
| Problem | Answer |
|---|---|
| 43 * 45 | 48 |
| 22 * 21 | 23 |

📝 Note: Ensure to practice problems where the exponents involve different bases or mixed terms as well.
2. The Quotient Rule Worksheet


The Quotient Rule worksheet covers the rule for dividing exponents:
(am) / (an) = a(m-n)
This worksheet provides exercises to help you:
- Divide expressions with same bases
- Understand when you cannot apply this rule (bases must be the same)
- Handle fractional exponents
📝 Note: Pay attention to when the base numbers differ; the quotient rule does not apply here.
3. The Power Rule Worksheet


Power Rule is another core rule for exponents, where you raise an exponent to another power:
(am)n = a(mn)
Here are some exercises you might encounter:
- (52)3
- (x3)2
These exercises help solidify the understanding of exponential growth and how to distribute powers.
📝 Note: This rule can also be used in reverse to break down exponents into simpler forms.
4. Negative and Zero Exponent Rules Worksheet


The fourth worksheet deals with exponents that are negative or zero:
a-m = 1/am
a0 = 1, when a ≠ 0
Practice problems include:
- Simplify 3-4
- Evaluate 70 + 50
This worksheet helps clarify concepts often misunderstood by students, like what happens when an exponent is zero or negative.
5. Fractional Exponents Worksheet


The final worksheet introduces fractional exponents, a concept that ties in with roots:
a1/n = n√a
am/n = (n√a)m
Here, learners will:
- Convert between roots and exponents
- Practice simplifying expressions with both numerator and denominator
- Learn to apply the rules in mixed contexts
📝 Note: Fractional exponents can appear complex but mastering them simplifies many higher-level math concepts.
In summary, mastering these five exponent rules worksheets will greatly enhance your understanding and proficiency in manipulating exponents. These rules form the bedrock of algebraic simplification, providing a structured path to solve complex mathematical problems. By practicing with these worksheets, you'll not only boost your math skills but also develop a deeper appreciation for how mathematical concepts interconnect and build upon each other.
Why are exponent rules important?

+
Exponent rules provide a methodical way to simplify expressions, making it easier to solve equations and understand mathematical concepts in various fields.
Can I use exponent rules with different bases?

+
Yes, but only the quotient rule and product rule can be directly applied when the bases are the same. For different bases, you might need to use logarithms or change of base formula.
How do negative exponents work?

+
Negative exponents indicate the reciprocal of the base to the power of the positive exponent. For example, a-m equals 1/am.