5 Simple Strategies for Mastering Exponents Division Worksheet

Mastering the division of exponents is a cornerstone skill in algebra that can be quite challenging for many students. Whether you're a student trying to excel in your math class or someone revisiting foundational mathematical concepts, understanding how to handle exponents efficiently can significantly enhance your problem-solving capabilities. Here, we delve into five simple strategies that will make dividing exponents a breeze. Let's explore how you can become proficient in this area with ease.
Understanding Exponent Division

Before diving into the strategies, let's clarify what exponent division entails. When you divide two exponents with the same base, you subtract the exponent of the denominator from the exponent of the numerator:
- Base is the same: a^m / a^n = a^{(m-n)}
- Example: 2^5 / 2^2 = 2^{5-2} = 2^3 = 8
🚨 Note: This rule only applies when the bases are identical.
Strategy 1: Visualize the Concept

Visual aids can significantly enhance understanding:
- Use diagrams or charts to represent exponential growth or division.
- Create a table to show how bases and exponents interact:
| Numerator Exponent (m) | Denominator Exponent (n) | Resultant Exponent (m-n) |
|---|---|---|
| 5 | 2 | 3 |
| 4 | 1 | 3 |
| 7 | 3 | 4 |

💡 Note: Visualizing can help conceptualize the process rather than just memorizing formulas.
Strategy 2: Use Exponent Identities

Leveraging exponent properties can simplify division:
- Zero Power Rule: Any number to the power of zero equals 1.
- Negative Exponent Rule: a^{-m} = 1/a^m
- Power of a Quotient Rule: (a/b)^n = a^n / b^n
By recognizing these properties, you can easily handle more complex problems:
- Example: 5^0 / 5^3 = 1 / 125
Strategy 3: Simplify Before Dividing
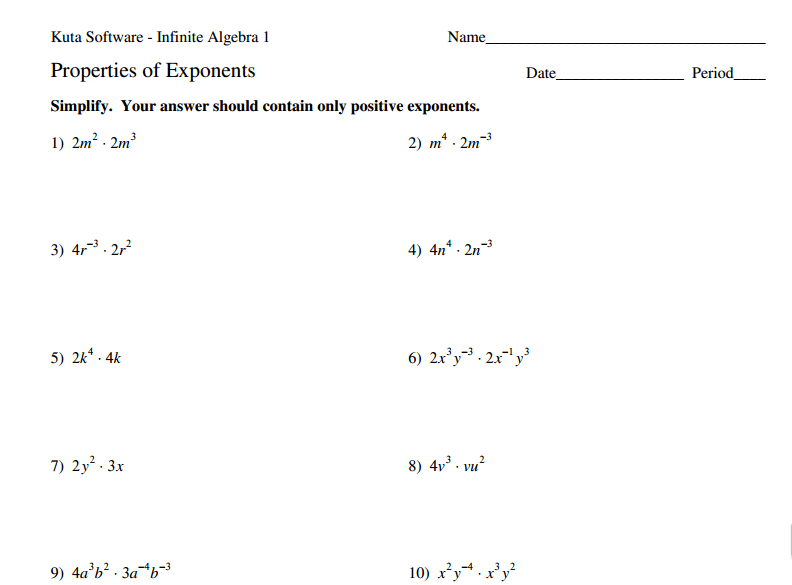
Simplification can make the division process easier:
- Break Down: Break large numbers into prime factors or easier terms.
- Example: (2^2 \cdot 3^3)^2 / 3^6 = 4 \cdot 27 / 729 = 108 / 729 = 4/27
🛠️ Note: Pre-simplification reduces the complexity of calculations.
Strategy 4: Practice with Worksheets

Consistent practice is key to mastery:
- Start with basic division worksheets and gradually increase the difficulty.
- Utilize online resources or create your own practice sheets.
Here are a few steps to practice:
- Begin with simple single-step problems.
- Move to multi-step problems involving simplification.
- Challenge yourself with real-world applications or word problems.
Strategy 5: Integrate Exponents into Problem-Solving
Apply exponent rules to real-life scenarios:
- Consider growth rates, depreciation, or geometric sequences.
- Example: Population Growth - P = P_0 \cdot e^{rt}
By solving practical problems, you're not only practicing but also understanding the significance of exponents in real-world contexts:
🌍 Note: Recognizing how exponents apply in various fields deepens your understanding and retention.
In summary, these five strategies provide a structured approach to mastering exponent division. By visualizing the process, understanding identities, simplifying calculations, practicing with worksheets, and integrating exponents into broader problem-solving, students can significantly enhance their algebraic proficiency. Remember, the key to success in math is consistent practice and application. Whether you're struggling or looking to refine your skills, these methods will guide you to excel in this essential mathematical concept.
What is the basic rule for dividing exponents with the same base?

+
The basic rule for dividing exponents with the same base is to subtract the exponent of the denominator from the exponent of the numerator. For instance, (a^m / a^n = a^{m-n}).
How can visual aids help in understanding exponent division?

+
Visual aids like diagrams or tables can help illustrate how exponents work, making abstract mathematical concepts more concrete and easier to understand.
Why should one simplify before dividing exponents?

+
Simplification can reduce the complexity of calculations, allowing for faster and more error-free solutions. It also helps in recognizing patterns or using exponent identities more effectively.