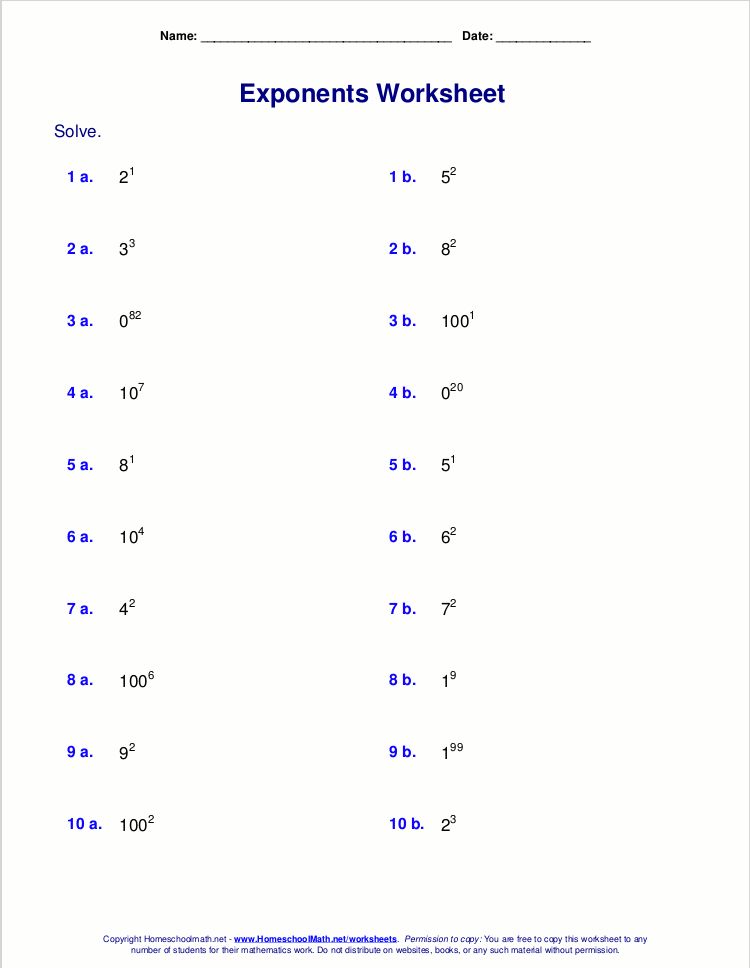
Master Exponential Word Problems with Our Fun Worksheet

Word problems can be a daunting task for many students, especially when they involve exponential growth or decay. However, understanding these problems is crucial, not only for acing math exams but also for real-world applications such as finance, biology, and physics. In this blog post, we'll explore how you can master exponential word problems through the use of a specially designed exponential word problem worksheet that makes learning both engaging and efficient.
The Importance of Exponential Growth and Decay

Exponential functions are everywhere around us. Whether it’s the growth of an investment, the decay of a substance, or the spread of diseases, exponential models help predict future behaviors. Here are some real-life applications:
- Finance: Compound interest and investment growth.
- Biology: Population growth, bacterial growth, or the spread of infectious diseases.
- Physics: Radioactive decay and cooling/heating of objects.
Why Word Problems?
Word problems challenge students to translate real-world scenarios into mathematical expressions. They require:
- Interpretation of the problem context.
- Setting up equations based on given information.
- Solving these equations to find meaningful results.
Understanding the Worksheet

Our worksheet designed for mastering exponential word problems includes:
- Diverse scenarios - each problem is set in a unique context to keep students engaged.
- Gradual difficulty increase - to cater to all skill levels.
- Visual aids - to help visualize the problem and solution.
Steps to Master Exponential Word Problems

Here’s a structured approach to solve these problems:
1. Identify the Key Information

- Determine what variable you are solving for.
- Identify if the problem involves exponential growth or decay.
- Look for constants like the initial amount, growth/decay rate, and time period.
🔍 Note: Always check for units of time to ensure consistency in your calculations.
2. Write Down the Basic Exponential Formula
The standard form for exponential growth/decay is:
[ A = A_0 \cdot e^{rt} ]- A - Final amount after time t .
- A_0 - Initial amount at time t = 0 .
- e - Euler's number (approximately 2.718).
- r - Rate of growth (positive) or decay (negative).
- t - Time passed.
3. Set Up the Equation

Translate the given information into this formula, substituting known values:
- If growth or decay rate is given as a percentage, convert it to decimal form.
- Identify if time is continuous or discrete and adjust the formula accordingly.
4. Solve for the Unknown

Often, you’ll need to:
- Isolate the unknown variable.
- Use logarithms or natural logarithms (ln) to solve for ( t ) or ( r ).
5. Interpret the Result

Remember to interpret your result back into the context of the problem:
- Verify the units of time.
- Check if the result makes sense in the real-world scenario.
To provide a practical example, let's work through a problem using our worksheet:
| Problem | Solution |
|---|---|
| A population of 10,000 rabbits grows at a rate of 10% per year. What will the population be in 5 years? |
|

Exponential word problems can be a powerful tool for understanding the world around us. By using the structured approach outlined in our worksheet, students not only improve their mathematical skills but also develop critical thinking and problem-solving abilities that are essential for future academic and professional success. This methodical process ensures that learners of all levels can approach these problems with confidence.
What is the difference between exponential growth and exponential decay?

+
Exponential growth involves an increasing rate where the quantity grows by a consistent percentage over a period. Exponential decay, on the other hand, sees the quantity decrease by a constant percentage over time.
Can the exponential formula be used for non-annual rates?

+
Yes, the formula can be adjusted for different time periods. For example, if you’re dealing with monthly growth, divide the annual rate by 12 or use ( \frac{r}{12} ) for monthly calculations.
What if I encounter a problem with natural logarithms?

+
Natural logarithms (ln) are used when solving exponential equations, particularly for time or rate. The formula ( t = \frac{\ln\left(\frac{A}{A_0}\right)}{r} ) helps solve for time when the final amount and initial amount are known.