Exponential Functions Worksheets: Practice and Master Now

In the realm of algebra, understanding and mastering exponential functions can be a gateway to deeper mathematical explorations and real-world applications. These functions, often presented in the form y = a \cdot b^x , where a is the initial value, b is the base, and x is the exponent, are fundamental in fields ranging from finance to physics, biology, and computer science. This blog post is dedicated to providing you with a comprehensive guide on how to practice and master exponential functions through specially designed worksheets.
Understanding Exponential Functions
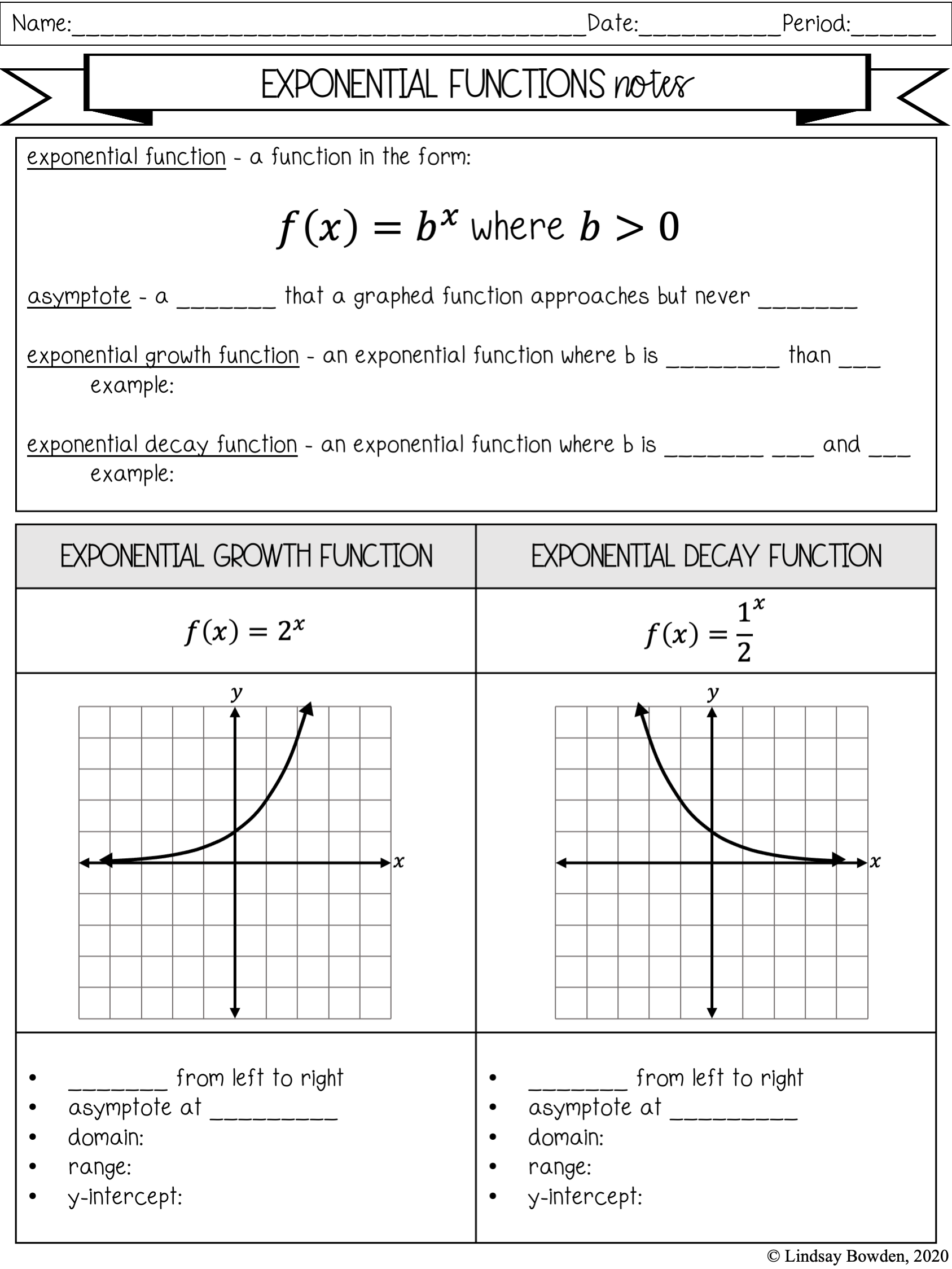
Before diving into the worksheets, let's first ensure you have a solid understanding of exponential functions:
- Definition: An exponential function is a mathematical expression where the variable appears in the exponent. The basic form is y = a \cdot b^x .
- Properties:
- The base b must be greater than 0 and not equal to 1 for the function to be defined for all real x .
- The graph of an exponential function will either grow (if b > 1 ) or decay (if 0 < b < 1 ) asymptotically towards the x-axis.
- The initial value a affects the y-intercept, while the base b determines the rate of growth or decay.

Exponential Functions Worksheets: Step-by-Step Guide

Here is a structured approach to help you practice and master exponential functions:
1. Basic Identification and Graphing

Begin with worksheets focused on identifying and graphing basic exponential functions:
- Identify the parameters ( a ), ( b ), and ( x ) in given functions.
- Plot points for the function and sketch its graph.
- Determine whether the function grows or decays based on the base ( b ).
2. Solving Exponential Equations

Move on to solving equations that involve exponential functions:
- Work with problems where you need to find ( x ) for a given ( y ) value.
- Practice natural logarithms for base ( e ) and common logarithms for other bases.
Example:
Solve for x in the equation 2^x = 32 . Using logarithms, we get:
\[ \log_2(32) = x \] \[ x = 5 \]📝 Note: Ensure you understand both logarithmic and algebraic methods to solve these equations for different bases.
3. Applications of Exponential Functions

Apply what you’ve learned to real-world scenarios:
- Compound Interest: Solve problems involving compound interest using the formula ( A = P \left(1 + \frac{r}{n}\right)^{nt} ).
- Population Growth: Calculate how populations or quantities grow or decay over time.
- Decay Models: Use exponential decay to model phenomena like radioactive decay or cooling.
4. Graph Transformations

Work with transformations to understand how changes in the parameters affect the graph:
- Horizontal and vertical shifts.
- Reflections over axes.
- Vertical and horizontal stretching or compression.
5. Advanced Practice

Once you’re comfortable with basic concepts, delve into:
- Logistic growth models.
- Combining exponential functions with other types of functions for more complex models.
| Concept | Example Problem | Worksheet Level |
|---|---|---|
| Basic Graphing | Graph y = 2^x | Beginner |
| Exponential Equations | Solve 3^x = 243 | Intermediate |
| Compound Interest | Calculate A for P = $1000 , r = 5\% , n = 4 , t = 2 | Advanced |
| Graph Transformations | Transform y = e^x by horizontal shift | Advanced |

By systematically going through these worksheet levels, you build a strong foundation in exponential functions, enabling you to tackle more complex mathematical problems or applications with ease.
In wrapping up this guide to mastering exponential functions through worksheets, remember that practice is key. Exponential functions appear in numerous real-world applications, making their mastery not only beneficial but essential for understanding growth, decay, and change over time in various fields. From finance to biology, the ability to work with these functions opens up a multitude of analytical opportunities. Continuously revisiting these worksheets, coupled with real-world problem-solving, will ensure a deep understanding and confident application of exponential functions in all your mathematical endeavors.
What is an exponential function?

+
An exponential function is of the form ( y = a \cdot b^x ), where ( a ) is a non-zero constant, ( b ) is a positive base different from 1, and ( x ) is a variable exponent. These functions model rapid growth or decay.
How do I solve an exponential equation?

+
One common approach is to take the logarithm of both sides to solve for ( x ). For example, to solve ( b^x = c ), you could use ( \log_b(b^x) = \log_b© ), leading to ( x = \frac{\log_b©}{\log_b(b)} ).
What real-world applications use exponential functions?

+
Exponential functions are used in finance (compound interest), biology (population growth), physics (radioactive decay), economics, epidemiology (spread of diseases), and many more fields.