5 Essential Exponent Rules Worksheet Tips
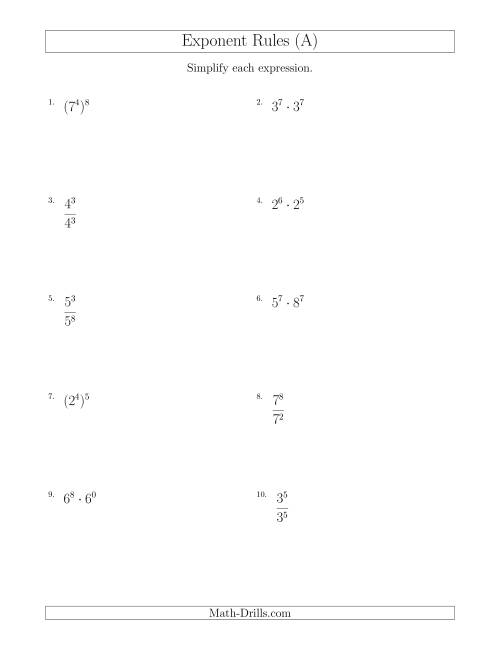
If you've ever found yourself grappling with math, particularly with the concept of exponents, you're not alone. Exponents, or powers, might seem straightforward at a glance, but they can get quite intricate when you dive deeper into their rules. In this post, we'll explore five essential tips for tackling exponent rules worksheets effectively. These tips are designed to not only help you understand the core concepts but also to make you adept at solving complex problems related to exponents.
1. Understand the Basics

Before jumping into advanced exponent rules, make sure you’re well-versed in the basic principles:
- The Zero Rule: Any non-zero number raised to the power of 0 equals 1. e.g., (3^0 = 1)
- The One Rule: Any number raised to the power of 1 is itself. e.g., (7^1 = 7)
- The Negative Rule: A negative exponent means the base is reciprocated, then raised to the positive exponent. e.g., (2^{-3} = \frac{1}{2^3} = \frac{1}{8})
- The Fraction Rule: When raising a fraction to an exponent, you raise both the numerator and the denominator to that exponent. e.g., ((\frac{2}{5})^2 = \frac{2^2}{5^2} = \frac{4}{25})
📝 Note: Always remember these fundamental rules, as they form the basis for more complex calculations.
2. Know Your Exponent Properties

Understanding the properties of exponents will help you simplify expressions quickly. Here are some key properties:
- Product of Powers: If you multiply two numbers with the same base, add their exponents. e.g., (5^3 \times 5^4 = 5^{3+4} = 5^7)
- Quotient of Powers: When dividing, subtract the exponents if the bases are the same. e.g., (\frac{3^6}{3^4} = 3^{6-4} = 3^2)
- Power of a Power: When you raise an exponent to another power, multiply the exponents. e.g., ((2^3)^2 = 2^{3 \times 2} = 2^6)
- Power of a Product: You can distribute the exponent to each factor. e.g., ((xy)^3 = x^3 y^3)
- Power of a Quotient: The exponent goes on both the numerator and the denominator. e.g., ((\frac{a}{b})^4 = \frac{a^4}{b^4})
🔍 Note: Practice these properties regularly to make your calculations seamless and efficient.
3. Learn to Identify Common Exponent Forms

Certain forms of exponents appear frequently in math problems. Recognizing these forms will speed up your problem-solving:
- Perfect Squares and Cubes: Knowing the squares and cubes of numbers from 1 to 15 can simplify many calculations. e.g., (3^2 = 9), (4^3 = 64)
- Roots as Powers: Roots can be written as exponents with fractional powers. e.g., (\sqrt[3]{8} = 8^{\frac{1}{3}} = 2)
- Negative Exponents: Understand how to simplify expressions involving negative exponents by moving the term with the negative exponent to the other side of the fraction. e.g., (2^{-3} = \frac{1}{2^3} = \frac{1}{8})
| Exponent Form | Equivalent |
|---|---|
| a^{1/n} | \sqrt[n]{a} |
| a^{m/n} | \sqrt[n]{a^m} |
📚 Note: Familiarity with common forms reduces the need for computation and enhances your speed.
4. Practice Simplifying Expressions

Real proficiency comes with practice. Here are some steps to help you simplify expressions:
- Rewrite the expression: Identify any bases and exponents you can simplify or combine.
- Apply properties: Use the properties of exponents to simplify your expression. This might involve multiplying, dividing, or distributing exponents.
- Watch for signs: Exponents can change signs, especially in negative exponent scenarios.
- Check your work: Double-check that you’ve applied the rules correctly.
💡 Note: Regular practice of these steps will reinforce your understanding and make complex problems less intimidating.
5. Use Mnemonics and Visualization

Memory aids like mnemonics can be incredibly helpful when working with exponents:
- Negative Exponents: Use “To the negative, up in the attic” to remember to move a term with a negative exponent to the top (or bottom) of a fraction.
- Product/Quotient Rules: “When multiplying powers, add the exponents; when dividing powers, subtract the exponents.”
🧠 Note: Mnemonics simplify learning and can help when you're under time pressure in exams.
In summary, mastering exponent rules isn’t just about memorizing formulas. It’s about understanding the logic behind these rules, practicing consistently, recognizing common forms, and using memory aids effectively. By applying these tips, you’ll not only excel in exponent-related worksheets but also develop a deeper appreciation for how exponents work in the broader context of mathematics. Let these tips guide your practice, and watch as your skills in exponent manipulation flourish.
Why do I need to know the rules of exponents?

+
Understanding exponent rules allows you to simplify expressions, solve equations more quickly, and work with logarithms, polynomial functions, and calculus. They are fundamental in advanced mathematics and science.
What’s the best way to practice exponent rules?
+
The best approach includes regular practice with worksheets, online quizzes, and problem sets. Try to work through problems without looking at the rules until you internalize them.
Can I use a calculator for exponent calculations?

+
Calculators can be used, but understanding how to manually calculate and simplify expressions with exponents is crucial for developing mathematical reasoning and for situations where calculators aren’t available.