5 Simple Tricks for Mastering Exponent Practice

If you're gearing up for an exam or just trying to master a specific mathematical topic, understanding exponents can be quite an empowering tool. Exponents, often called powers, are not just about mastering quick computation; they reveal patterns, facilitate simplification of algebraic expressions, and help understand the world of exponential growth and decay. Let's dive into five simple yet effective techniques to turn exponent practice into an art.
Understanding The Basics of Exponents

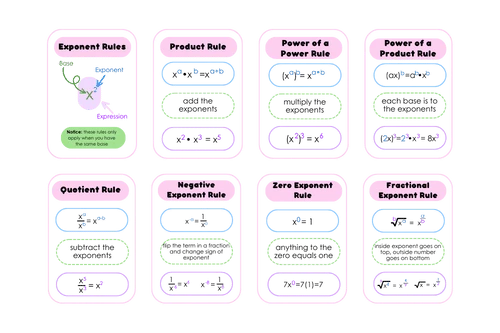
Before delving into the tricks, it's crucial to understand the basic rules of exponents:
- Multiplication of Powers: When you multiply powers with the same base, you add their exponents.
- Division of Powers: When dividing powers with the same base, subtract the exponent of the denominator from the numerator.
- Power to a Power: To raise a power to another power, multiply the exponents.
- Zero Power: Any non-zero number raised to the power of zero equals one.
- Negative Powers: A negative exponent means the reciprocal of that number with a positive exponent.
Trick 1: Use Visual Representation


One of the most engaging ways to understand exponents is through visual representation. Draw out an exponential tower or use manipulatives like blocks or dice to illustrate the physical representation of, say, 2^3 being equivalent to two stacked three times. This technique aids in grasping the concept:
- It helps in visualizing how numbers grow exponentially.
- It makes abstract math more concrete and easier to comprehend.
📝 Note: Drawing or using physical models not only aids in understanding but also acts as a memory hook for later recall.
Trick 2: Play with Patterns

Numbers follow patterns, and so do exponents. Here are some pattern-based tips:
- Pattern Recognition: Notice how each power of a number follows a predictable pattern. For instance, 2^0=1, 2^1=2, 2^2=4, 2^3=8, and so on. Recognize these patterns to speed up calculations.
- Exponent Table: Creating a small table can be extremely helpful:
| Number | Power of 2 | Power of 3 |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 2 | 3 |
| 2 | 4 | 9 |
| 3 | 8 | 27 |

📈 Note: Recognizing these patterns can significantly reduce the time needed for exponentiation by hand.
Trick 3: Flashcards and Speed Drills

Nothing beats practice. Use flashcards or an app:
- Create Flashcards: Write down base numbers on one side and their powers on the other. Test yourself or others with these.
- Speed Drills: Set a timer for 5-minute sessions where you practice various exponent problems, gradually increasing the difficulty.
Trick 4: Relate Exponents to Real-World Scenarios

Exponents are not just numbers; they have real-world applications:
- Population Growth: Model population growth with exponents to understand how quickly numbers can escalate.
- Compound Interest: Use exponents to calculate future value with compound interest.
By associating exponents with tangible outcomes, their practical importance becomes clearer, enhancing both comprehension and retention.
Trick 5: Reverse Engineer Problems

Start with the answer and work backward:
- Inverse Problems: Instead of finding 4^3, start with 64 and find the numbers that, when cubed, equal 64.
- Problem Solving: This technique helps in understanding how exponents interact with each other in equations.
When you engage with exponents from a different perspective, you uncover new insights and solidify your knowledge.
Remember, mastering exponents is a journey of understanding patterns, applying rules, and visualizing growth. With these tricks, you're not just memorizing; you're learning to think mathematically, which is a skill that extends far beyond any single topic in math.
Why do we need to learn exponents?
+
Exponents are fundamental in algebra, calculus, and other areas of mathematics. They help in simplifying expressions, solving complex equations, and understanding growth models in sciences like physics, biology, and finance.
Can visual methods really help in understanding exponents?

+
Visual aids provide a concrete understanding of abstract concepts. By physically seeing how exponents work, students can internalize these concepts more effectively.
Are there any other methods to practice exponents?

+
Yes, besides these tricks, practicing with real-world data, using educational software, and engaging in peer discussions are also very effective.