5 Tricks to Master Exponent Expressions Fast
The world of mathematics can often seem like an intricate puzzle, with various expressions and operations each serving unique purposes. Among these, exponent expressions stand as one of the fundamental pillars, widely used in algebra, calculus, and many other branches of mathematics and sciences. Yet, for many students and professionals, mastering exponent expressions remains a challenging task. In this blog post, we will delve into 5 Tricks to Master Exponent Expressions Fast, ensuring that you can handle these with confidence and accuracy.
Understanding the Basics

Before diving into the tricks, a solid understanding of what exponents represent is crucial:
- Exponentiation is the mathematical operation where a number, called the base, is raised to the power of another number, the exponent or power.
- The general form of an exponential expression is (a^n), where (a) is the base and (n) is the exponent.
📌 Note: Remember that the exponent tells you how many times the base is to be multiplied by itself.
Trick 1: The Power of Zero

One of the simplest yet often misunderstood exponent rules is:
- Any number raised to the power of zero equals one ((a^0 = 1))
This can be counterintuitive at first, but consider this logical progression:
| Expression | Result |
|---|---|
| (12^3 = 12 \times 12 \times 12) | 1728 |
| (12^2 = 12 \times 12) | 144 |
| (12^1 = 12) | 12 |
| (12^0 = ?) | 1 |
As you can see, the result gets smaller as the exponent decreases, reaching the identity element of multiplication (1) when the exponent is zero.
📌 Note: This rule holds for all non-zero numbers, even for fractions and negative numbers.
Trick 2: Negative Exponents

A negative exponent signifies a reciprocal operation:
- Any number raised to a negative power results in one over the number raised to the positive power of that exponent.
- Mathematically, (a^{-n} = \frac{1}{a^n})
Here’s how this works:
| Expression | Result |
|---|---|
| (3^{-1}) | (\frac{1}{3}) |
| (5^{-2}) | (\frac{1}{25}) |
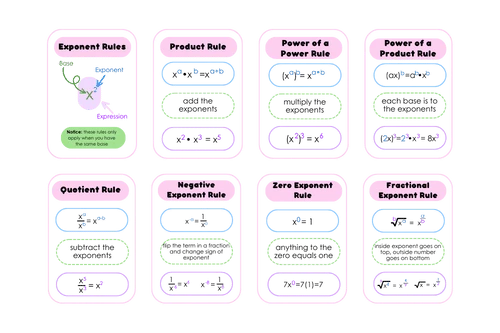
Trick 3: Exponent Products and Quotients

When dealing with exponents in multiplication or division, you can use these rules:
- Product of Powers: When multiplying exponents with the same base, add the exponents. (a^m \times a^n = a^{m+n})
- Quotient of Powers: When dividing exponents with the same base, subtract the exponents. (a^m \div a^n = a^{m-n})
Here are some examples:
| Operation | Expression | Result |
|---|---|---|
| Multiplication | (2^3 \times 2^4) | (2^{3+4} = 2^7 = 128) |
| Division | (3^6 \div 3^3) | (3^{6-3} = 3^3 = 27) |
Trick 4: Power to a Power

Exponents can be raised to another power:
- When an exponent is raised to another exponent, multiply the exponents. ((a^m)^n = a^{mn})
This is particularly useful when simplifying expressions:
| Expression | Simplification |
|---|---|
| ((3^2)^3) | (3^{2 \times 3} = 3^6 = 729) |
Keep in mind that these rules work for both positive and negative integers, but not for fractional exponents without additional rules.
📌 Note: Applying these rules correctly can significantly simplify complex expressions and calculations.
Trick 5: Fractional Exponents

Fractional or rational exponents introduce roots:
- A fractional exponent (a^{m/n}) is equivalent to taking the (n)-th root of (a) and then raising it to the (m)-th power.
- Mathematically, (a^{m/n} = (\sqrt[n]{a})^m)
Here’s an example:
| Expression | Equivalent Expression |
|---|---|
| (4^{1⁄2}) | (\sqrt{4} = 2) |
| (8^{2⁄3}) | ((\sqrt[3]{8})^2 = (2)^2 = 4) |
Fractional exponents provide a seamless way to integrate exponents with roots, making calculations involving these operations more straightforward.
In summary, mastering exponent expressions doesn’t need to be an overwhelming task. By understanding the basic rules, utilizing the power of zero, handling negative exponents, simplifying expressions through products and quotients, applying powers to powers, and incorporating fractional exponents, you can approach even the most complex expressions with confidence. These five tricks will not only save you time but also provide a clear pathway to tackling higher mathematics with precision and ease.
What is the significance of zero as an exponent?

+
Zero as an exponent always equals 1 for any non-zero number because it represents the multiplicative identity. It’s useful in various mathematical and scientific contexts, like calculus.
How do you simplify ((5^2 \times 5^3) / 5^4)?
+
Using the rules mentioned, ((5^{2+3}) / 5^4 = 5^5 / 5^4 = 5^{5-4} = 5)
What does a negative exponent mean?

+
A negative exponent implies taking the reciprocal of the base raised to the positive equivalent of that exponent, essentially a “flip” over the denominator.