5 Tips to Identify Even and Odd Functions Easily

Recognizing whether a mathematical function is even, odd, or neither can be a fundamental skill in algebra and calculus. This knowledge not only simplifies the analysis of functions but also has practical applications in various fields like signal processing, engineering, and physics. Here are five insightful tips to help you identify even and odd functions with ease:
Understanding Function Symmetry

One of the primary methods to determine if a function is even or odd is to understand its symmetry:
- Even Functions: These are symmetric about the y-axis. Visually, if you were to fold the graph along the y-axis, both halves would match up perfectly. Mathematically, a function f(x) is even if f(x) = f(-x).
- Odd Functions: These functions are symmetric about the origin. If you rotate the graph 180 degrees, the graph would still look the same. Mathematically, a function f(x) is odd if f(x) = -f(-x).

✏️ Note: Some functions might look symmetrical but are neither even nor odd because they might not fit the exact definitions perfectly.
Testing the Function

To practically identify if a function is even or odd, use these steps:
- Start with the function f(x).
- Calculate f(-x).
- Compare f(x) to f(-x) for even functions or -f(-x) for odd functions.
| Function Type | Condition |
|---|---|
| Even | f(x) = f(-x) |
| Odd | f(x) = -f(-x) |

Algebraic Properties

Understanding some algebraic properties can also be useful:
- Even functions: For example, if f(x) is a polynomial with only even powers, it's even.
- Odd functions: Polynomials with only odd powers are odd.
- The sum of two even functions is even, the sum of two odd functions is odd, but the sum of an even and an odd function is neither.
📚 Note: Remember, the composition or product of functions might change their even/odd characteristics.
Using Known Examples

Familiarize yourself with some common functions known to be even or odd:
Examples of Even Functions:

- f(x) = x²
- f(x) = cos(x)
- f(x) = e^|x|
Examples of Odd Functions:

- f(x) = x³
- f(x) = sin(x)
- f(x) = tan(x)
By understanding these examples, you can quickly recognize the properties of other functions by comparison.
Evaluating Specific Points

Another approach is to evaluate the function at specific points:
- For even functions, evaluating at f(2) and f(-2) should yield the same result.
- For odd functions, f(3) should be negative of f(-3).
This method can sometimes provide a quick insight when symmetry and testing are not straightforward.
By employing these five strategies, you'll be well-equipped to determine the evenness or oddness of any given function quickly and accurately. Understanding these principles not only helps in academic settings but also in practical applications where symmetry in functions plays a crucial role. Remember that recognizing these characteristics can greatly simplify complex mathematical operations and enhance your analytical skills in diverse areas of study and work.
Can a function be both even and odd?
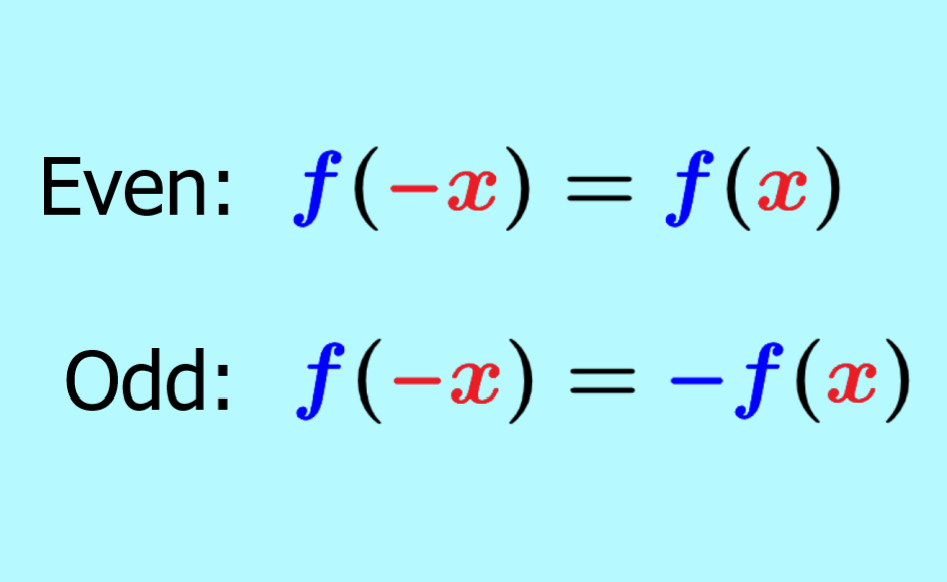
+
No, a function cannot be both even and odd at the same time because the definitions are mutually exclusive. An even function is symmetric about the y-axis, whereas an odd function is symmetric about the origin. If f(x) = f(-x), it cannot also be that f(x) = -f(-x), except for the case when the function is identically zero, which satisfies both conditions trivially.
How do I handle a function that is neither even nor odd?

+
If a function does not satisfy the conditions for being even or odd, you can still analyze its properties like continuity, limits, or perform transformations, but for symmetry-based analysis, it won’t be as straightforward. Sometimes, you can express the function as a sum of an even and an odd component for easier analysis.
Is it possible for a polynomial function to be neither even nor odd?

+
Yes, a polynomial can be neither even nor odd if it contains both even and odd powers of x, or if the degrees of terms do not allow for a clear symmetry, like f(x) = x^3 + x or f(x) = x^4 + x.