7 Ways to Master Equivalent Ratios in 6th Grade

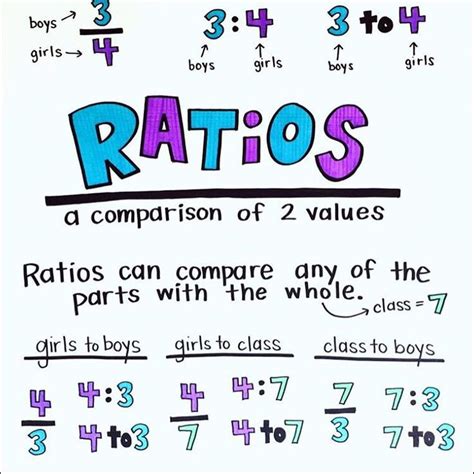
Unlocking the Secrets of Equivalent Ratios

Equivalent ratios are a fundamental concept in mathematics, and mastering them is crucial for 6th-grade students. In this article, we will explore seven ways to help you become proficient in equivalent ratios.
Understanding Equivalent Ratios

Before we dive into the seven ways, let’s start with the basics. Equivalent ratios are ratios that have the same value, but are expressed differently. For example, 2:3 and 4:6 are equivalent ratios because they represent the same relationship between two quantities.
1. Visualizing Equivalent Ratios with Diagrams

Using diagrams is an effective way to visualize equivalent ratios. By drawing diagrams, you can see the relationship between the different parts of the ratio. For example, if you have a ratio of 2:3, you can draw a diagram with 2 circles and 3 squares. This will help you understand that the ratio of circles to squares is 2:3.
Example:

| Ratio | Diagram |
|---|---|
| 2:3 | 2 circles, 3 squares |
| 4:6 | 4 circles, 6 squares |

2. Using Multiplication to Find Equivalent Ratios

Another way to find equivalent ratios is by using multiplication. If you multiply both numbers in a ratio by the same number, you will get an equivalent ratio. For example, if you multiply 2:3 by 2, you will get 4:6.
Example:

| Original Ratio | Multiplier | Equivalent Ratio |
|---|---|---|
| 2:3 | 2 | 4:6 |
| 3:4 | 3 | 9:12 |
3. Simplifying Ratios to Find Equivalent Ratios

Simplifying ratios is another way to find equivalent ratios. If you have a ratio with a common factor, you can simplify it by dividing both numbers by the common factor. For example, if you have a ratio of 6:8, you can simplify it by dividing both numbers by 2, resulting in a ratio of 3:4.
Example:
| Original Ratio | Simplified Ratio |
|---|---|
| 6:8 | 3:4 |
| 9:12 | 3:4 |
4. Identifying Equivalent Ratios in Real-Life Scenarios
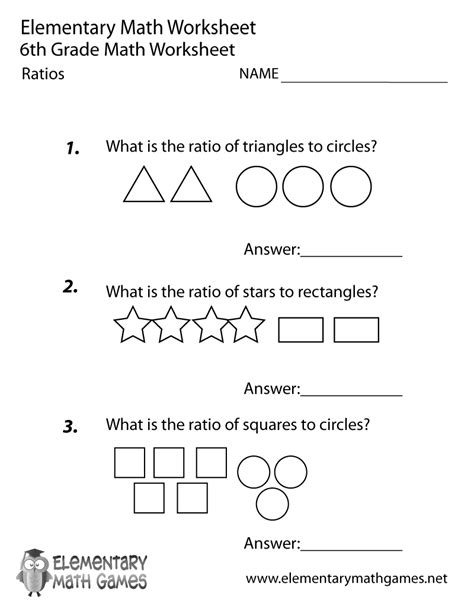
Equivalent ratios are not just limited to math problems. They appear in real-life scenarios, such as cooking, building, and science. Identifying equivalent ratios in these scenarios can help you understand the concept better.
Example:

- A recipe calls for a ratio of 2 cups of flour to 3 cups of sugar. If you want to make a larger batch, you can multiply the ratio by 2, resulting in 4 cups of flour to 6 cups of sugar.
- A building has a ratio of 3 windows to 4 doors. If you want to add more windows and doors, you can multiply the ratio by 2, resulting in 6 windows to 8 doors.
5. Practicing Equivalent Ratios with Word Problems
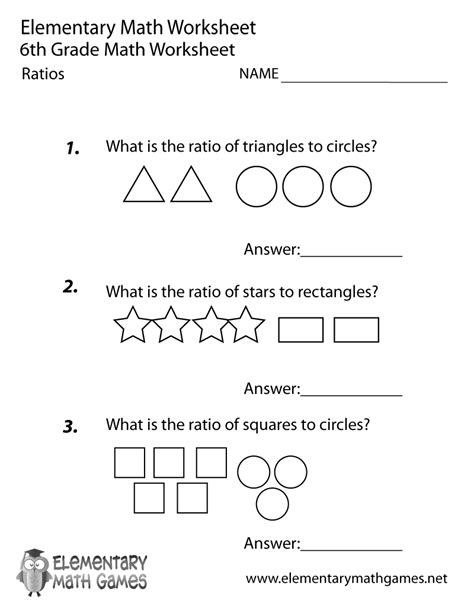
Practicing equivalent ratios with word problems can help you apply the concept to real-life scenarios. Word problems require you to read, understand, and solve problems that involve equivalent ratios.
Example:

- Tom has a bag of apples and bananas in a ratio of 2:3. If he adds 2 more apples and 3 more bananas, what is the new ratio of apples to bananas?
- A bakery sells a total of 240 muffins and cakes in a ratio of 3:5. How many muffins and cakes does the bakery sell?
6. Using Equivalent Ratios to Solve Problems

Equivalent ratios can be used to solve problems that involve proportions, scaling, and ratios. By applying the concept of equivalent ratios, you can solve problems that require you to find the missing value in a proportion.
Example:

- A map has a scale of 1:50,000. If a building is 2 cm tall on the map, how tall is it in real life?
- A recipe calls for a ratio of 2 cups of flour to 3 cups of sugar. If you want to make a batch that requires 4 cups of flour, how much sugar do you need?
7. Checking Your Work with Equivalent Ratios

Finally, checking your work with equivalent ratios can help you ensure that your answers are correct. By verifying that your answer is an equivalent ratio, you can be confident that your solution is accurate.
Example:

- If you solve a problem and get a ratio of 4:6, you can check your work by simplifying the ratio or multiplying it by a number to see if you get an equivalent ratio.
🤔 Note: Remember to always check your work by verifying that your answer is an equivalent ratio.
In conclusion, mastering equivalent ratios requires practice, patience, and persistence. By using these seven ways to master equivalent ratios, you can become proficient in this fundamental math concept and apply it to real-life scenarios.
What is an equivalent ratio?

+
An equivalent ratio is a ratio that has the same value, but is expressed differently.
How do I find equivalent ratios?

+
You can find equivalent ratios by multiplying both numbers in a ratio by the same number, simplifying a ratio with a common factor, or identifying equivalent ratios in real-life scenarios.
Why are equivalent ratios important?

+
Equivalent ratios are important because they help you understand proportions, scaling, and ratios, which are crucial concepts in mathematics and real-life scenarios.
Related Terms:
- Equivalent ratios Worksheet with Answers
- Equivalent ratios worksheet PDF
- 6th ratio problems with answers
- 6th grade ratios printable worksheets
- equivalent ratio worksheets grade 6
- ratios 6th grade worksheet pdf



