Equivalent Ratios Worksheet: Master Math Ratios Easily

In the realm of mathematics, understanding ratios is fundamental to solving various types of problems, from simple proportions to complex equations. Equivalent ratios are an essential part of this, allowing students to manipulate and comprehend ratios in different contexts. This blog post will guide you through what equivalent ratios are, why they are important, and how you can master them with ease using a worksheet method.
Understanding Equivalent Ratios

Equivalent ratios are simply different ways of expressing the same comparison of two numbers or quantities. For example, the ratio 2:3 is equivalent to 4:6, 8:12, or even 2⁄3 in fractional form. This equivalence means that each part of the whole is divided into the same relative parts:
- 2 out of 3 is the same as 4 out of 6, etc.
Understanding this concept allows you to compare quantities and sizes, whether you’re mixing ingredients in cooking or scaling down measurements for a blueprint.
Why Equivalent Ratios Matter

Ratios come into play in many real-world applications:
- Financial analysis: Companies use ratios to compare financial metrics over different periods or against competitors.
- Cooking: Recipes need to be adjusted for different numbers of servings or different ingredient quantities.
- Graphic Design: Scaling images or layouts proportionally is crucial.
- Science and Engineering: Ratios help in making scale models, determining concentration of solutions, or even understanding ratios in electrical circuits.
Being adept at finding equivalent ratios is not just about passing math tests; it’s about navigating life with better problem-solving skills.
Mastering Equivalent Ratios with a Worksheet

The best way to solidify your understanding of equivalent ratios is through practice. Here’s how to use a worksheet effectively:
Step 1: Choose a Worksheet
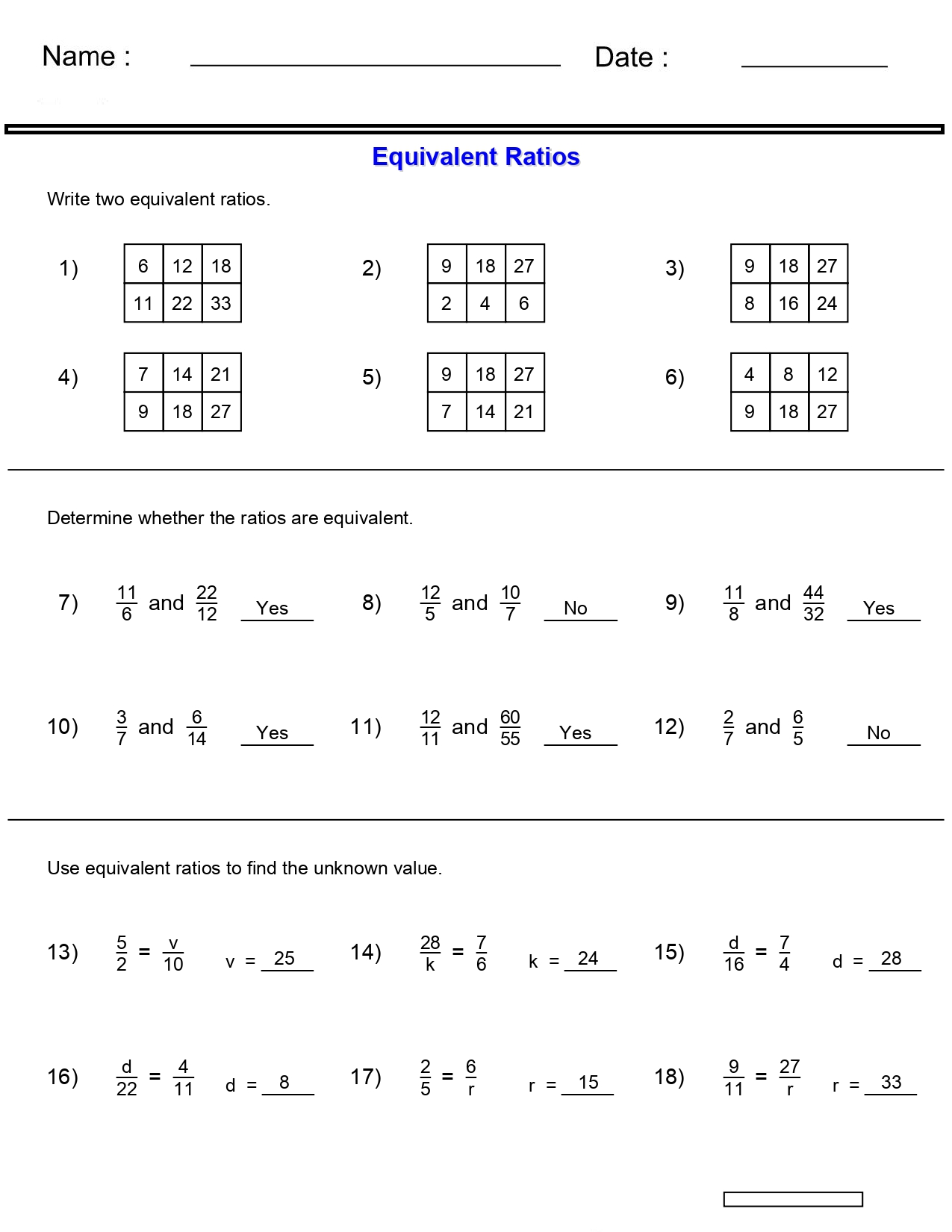
Select a worksheet that includes problems on finding equivalent ratios. Here are some types of problems you might encounter:
- Identifying equivalent ratios from a set of options.
- Converting one ratio into an equivalent one.
- Finding multiple equivalent ratios for a given ratio.
Step 2: Understand Each Problem

Before solving, read through the problem carefully to identify:
- The given ratio or the ratio you need to find an equivalent for.
- Whether there are constraints or specific instructions (like converting to simplest form).
Step 3: Solve the Problem

To find equivalent ratios:
- Multiply or divide both parts of the original ratio by the same number (to keep the ratio unchanged).
- If you need to simplify, find the greatest common divisor (GCD) of the two numbers in the ratio.
Here’s an example:
| Given Ratio | Process | Equivalent Ratios |
|---|---|---|
| 2:3 | Multiply by 2 | 4:6 |
| 2:3 | Divide by 2 | 1:1.5 (or 2:3 in simplest form) |
| 2:3 | Multiply by 3 | 6:9 |

Step 4: Check Your Work

After solving:
- Ensure your equivalent ratios retain the same proportion.
- Check for simplification if required by the problem.
💡 Note: Always double-check if the simplified version of a ratio matches the original to ensure you haven't altered the proportion.
Common Mistakes to Avoid

When working with equivalent ratios, common pitfalls include:
- Forgetting to multiply or divide both parts of the ratio by the same number.
- Not simplifying ratios when required.
- Not considering the context of the problem, which might change the interpretation of the ratios.
⚠️ Note: Remember that the order of the numbers in the ratio matters. Switching the order changes the ratio entirely.
In wrapping up this exploration of equivalent ratios, remember that practice is key. The more you work with ratios, the more intuitive the process becomes. Whether you’re scaling a recipe for a larger crowd or interpreting financial ratios for your company, understanding equivalent ratios equips you with the tools to make informed decisions. This knowledge isn’t just for math class; it’s a vital part of everyday life, enhancing your analytical skills and decision-making capabilities.
How do I know if two ratios are equivalent?

+
Two ratios are equivalent if one can be transformed into the other by multiplying or dividing both parts of the original ratio by the same number.
What’s the benefit of simplifying ratios?

+
Simplifying ratios makes them easier to compare and understand, especially in contexts where large numbers are involved.
Can equivalent ratios have decimals?

+
Yes, equivalent ratios can have decimals or fractions, as long as the proportion remains the same.
Why do I need to know about equivalent ratios?

+
Equivalent ratios are useful in numerous practical scenarios, from cooking to financial analysis, where scaling or understanding proportions is necessary.