5 Ways to Master Equivalent Fractions With Answers

Understanding the Concept of Equivalent Fractions

Equivalent fractions are essentially different expressions of the same portion or amount. For instance, think of 1⁄2, 2⁄4, and 3⁄6 as versions of the same idea - each representing half of a whole. Grasping the notion of equivalent fractions is key for numerous mathematical pursuits, from basic arithmetic to advanced algebra. Here’s a guide to mastering the art of working with equivalent fractions.

Method 1: Cross-Multiplying for Finding Equivalent Fractions
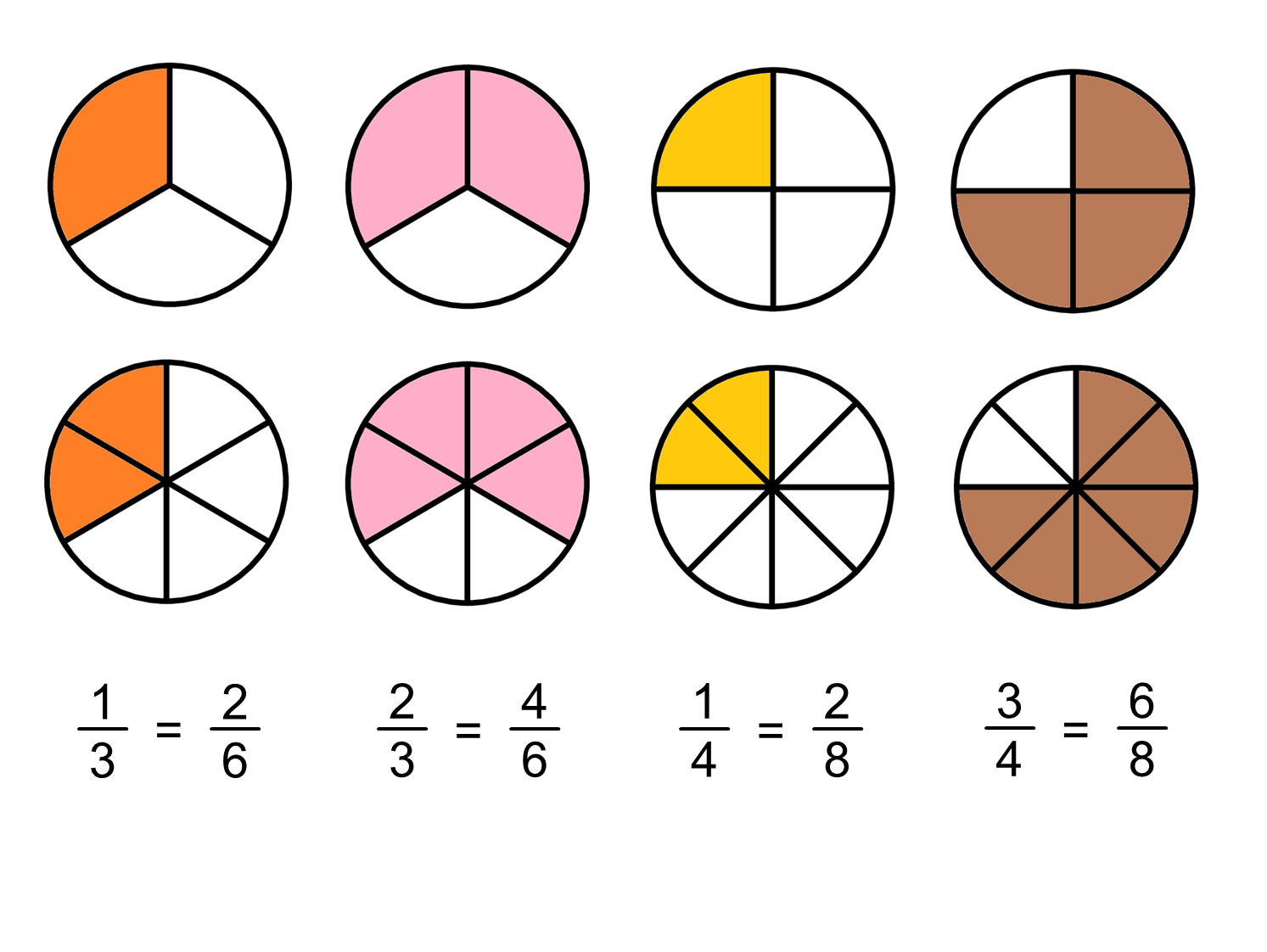
The cross-multiplication technique involves multiplying the numerator (top number) of one fraction with the denominator (bottom number) of the other. Here’s how:
- Take your starting fraction, let’s say 3⁄5.
- To find an equivalent fraction, select a multiplier. Suppose we want a multiple of 3, so we’ll multiply by 2.
- Multiply the numerator and denominator by this factor: (3 * 2) / (5 * 2) = 6⁄10.
This multiplication ensures that you preserve the value of the fraction.
Method 2: Reducing Fractions to Lowest Terms

Reducing fractions to their lowest terms involves dividing both the numerator and the denominator by a common factor until they can’t be divided any further:
- Suppose we have the fraction 12⁄16.
- Divide both numbers by 4 to obtain 3⁄4.
This simplification showcases how any fraction can be expressed in its most fundamental form.
Method 3: Using Fraction Strips or Visual Models

Visual aids like fraction strips or models can help in understanding equivalency:
- Imagine having a strip divided into 4 equal parts, each representing 1⁄4.
- If you color 3 of these 4 parts, you have 3⁄4 of the strip.
- Now, if you divide each of these 4 parts into 2, you have 8 smaller parts. 6 out of these 8 parts would still be equivalent to 3⁄4.
This visual approach aids in intuitive understanding of equivalence.
Method 4: Multiplication by a Common Denominator

To compare fractions, sometimes converting them to have a common denominator helps:
- Consider 3⁄5 and 4⁄7.
- Multiply both the numerator and denominator by 7 for 3⁄5: (3 * 7)/(5 * 7) = 21⁄35.
- Similarly, for 4⁄7, multiply both by 5: (4 * 5)/(7 * 5) = 20⁄35.
Now, you can easily see that 21⁄35 is greater than 20⁄35.
Method 5: Using Division to Find Equivalent Fractions

Sometimes, dividing the numerator and denominator by a common divisor simplifies the process:
- If we have 8⁄12, we can divide both by 4 to get 2⁄3.
- Or, we could also divide by 2 twice: (8⁄2)/(12⁄2) = 4⁄6, then (4⁄2)/(6⁄2) = 2⁄3.
This method shows the flexibility in manipulating fractions to achieve equivalence.
🧠 Note: Always verify your results by simplifying further if possible to maintain a reduced form of the fraction.
In this extensive exploration of equivalent fractions, you’ve been equipped with multiple approaches to mastering this fundamental math concept. From visual representations to algebraic techniques, you can now confidently manipulate fractions in various contexts, ensuring accuracy and understanding. Keep practicing with real-life examples, and soon, working with equivalent fractions will become second nature.
Why do we need to find equivalent fractions?

+
Understanding and finding equivalent fractions helps in comparing, adding, subtracting, and simplifying problems in mathematics. It provides a clear way to see that different fractions can represent the same value.
Is there an easier way to find equivalent fractions for large numbers?

+
For larger numbers, using prime factorization or the greatest common divisor (GCD) method can simplify the process significantly.
How do I know if two fractions are equivalent?

+
You can determine if two fractions are equivalent by:
- Cross-multiplying to check if the product of one fraction’s numerator and the other’s denominator equals the opposite.
- Reducing both fractions to their simplest forms and checking if they are the same.