Mastering Equivalent Fractions with Our Fun Worksheet

Equivalent fractions are fractions that represent the same value despite having different numerators and denominators. Understanding equivalent fractions is crucial as they are the foundation of many mathematical operations, including addition, subtraction, and comparison of fractions. In this comprehensive guide, we will explore how to master equivalent fractions with an engaging and educational worksheet. This post will take you through the process, provide practical examples, and offer insights into why this skill is essential for students and anyone interested in sharpening their math skills.
Understanding Equivalent Fractions
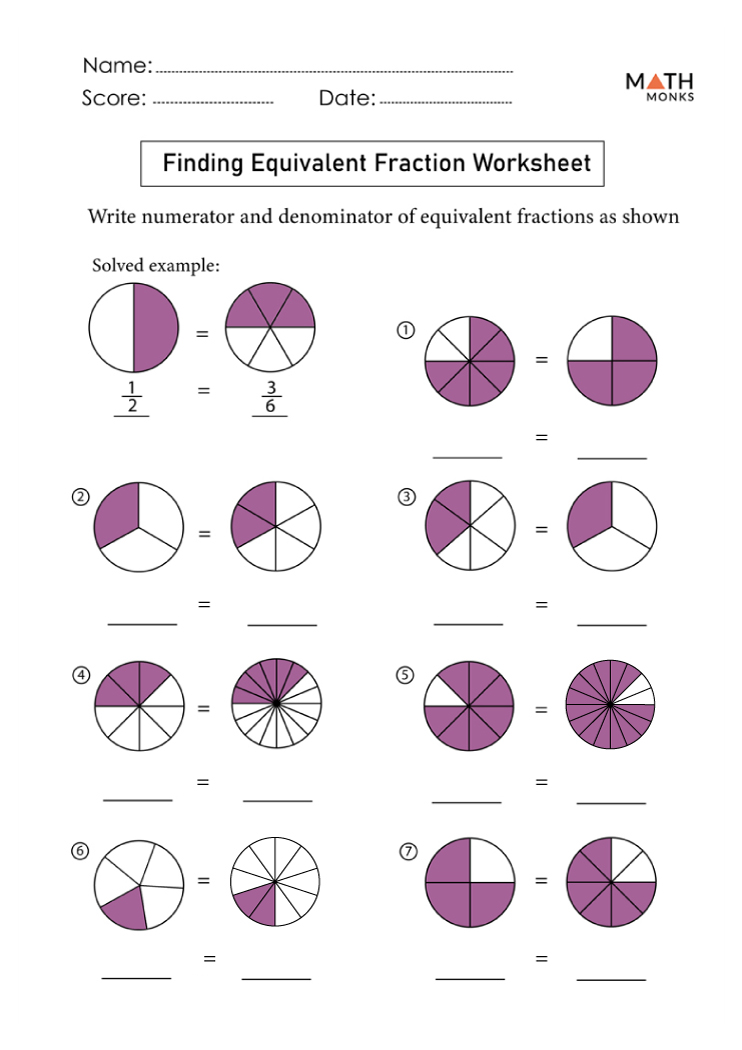
Before diving into the worksheet, it’s essential to understand what equivalent fractions are. By definition, two fractions are equivalent if they are on the same spot on the number line or have the same value when simplified. Here’s how you can find equivalent fractions:
- Multiply the numerator and the denominator by the same number: If you multiply or divide both the numerator and the denominator of a fraction by the same number (not zero), the value of the fraction does not change.
- Simplify or reduce to the simplest form: You can also find equivalent fractions by simplifying an existing fraction until you can't reduce any further.
💡 Note: Understanding the concept of equivalent fractions allows for easier manipulation of fractions in higher mathematics, algebraic expressions, and in daily life applications.
Creating a Fun Worksheet for Equivalent Fractions

A well-designed worksheet can make learning about equivalent fractions both fun and educational. Here are steps to create an effective worksheet:
1. Choose Age-Appropriate Content

Start by ensuring your worksheet aligns with the student’s skill level. For younger learners, use basic fractions like halves, quarters, and thirds. For older or more advanced students, incorporate more complex fractions.
2. Integrate Visual Aids
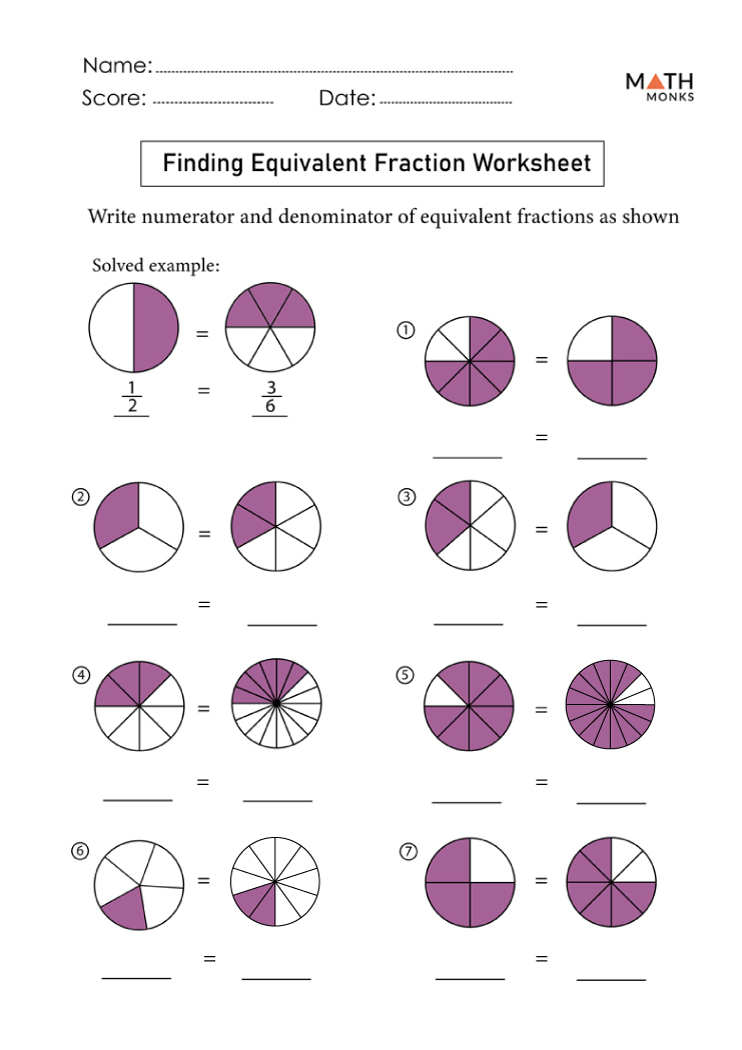
Visual aids like pie charts or bar models can help students grasp the concept of equivalence visually. Here’s an example:
| Fraction | Equivalent Fractions |
|---|---|
| 1⁄2 | 2⁄4, 3⁄6, 4⁄8 |
| 3⁄4 | 6⁄8, 9⁄12, 15⁄20 |

📌 Note: Visual aids not only make the worksheet appealing but also facilitate understanding through different learning styles.
3. Design Interactive Exercises

- Matching Games: Create cards with fractions on one side and their equivalents on the other for students to match.
- Fill-in-the-Blank: Provide students with fractions and ask them to fill in the blanks with equivalent fractions.
- Multiple Choice: Offer several options for equivalent fractions and ask students to choose the correct ones.
4. Include Real-Life Scenarios

Use real-world applications to make the concept more relatable:
- Ask students to calculate equivalent fractions when dividing a pizza into different slices.
- Use measurements like ingredients in recipes where fractions need to be adjusted to suit the number of servings.
Benefits of Mastering Equivalent Fractions

Mastering equivalent fractions has several advantages:
- Enhanced Problem-Solving Skills: Students become better at handling fractions, making them more adept at solving various mathematical problems.
- Improved Fraction Addition and Subtraction: Understanding equivalence is key when adding or subtracting unlike fractions.
- Critical Thinking Development: Recognizing and working with equivalent fractions develops logical and critical thinking.
Strategies for Teaching Equivalent Fractions
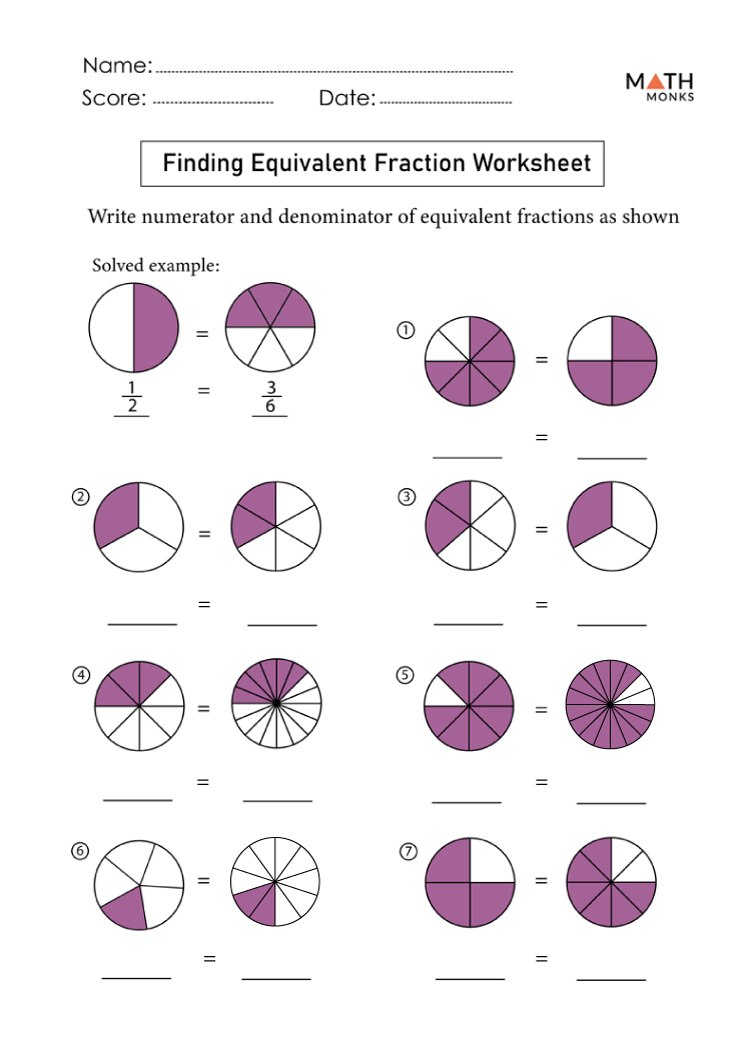
Here are some strategies educators can use to teach equivalent fractions effectively:
- Use Fraction Strips: Physical or digital fraction strips can show how different fractions are equivalent.
- Number Line: Plotting fractions on a number line helps visualize where equivalent fractions lie.
- Multiplication and Division: Explain how multiplying or dividing both parts of a fraction by the same number results in an equivalent fraction.
Incorporating these strategies into your teaching methods will reinforce the understanding of equivalent fractions, making the learning process both educational and enjoyable.
Key Takeaways from the Worksheet

After working through the worksheet, here are the essential points students should understand:
- The process of finding equivalent fractions through multiplication and division.
- The importance of equivalent fractions in performing arithmetic operations with fractions.
- Practical applications of equivalent fractions in everyday scenarios.
- How to visually represent and compare equivalent fractions.
🌟 Note: The mastery of equivalent fractions is not just about academics; it also has real-life implications in understanding proportions, recipes, measurements, and problem-solving skills in various disciplines.
To sum up, equivalent fractions are more than just a mathematical concept; they are a tool for understanding the world around us. By using a worksheet tailored to teach this topic in an engaging manner, students can quickly grasp the idea, apply it practically, and enhance their overall mathematical proficiency. This knowledge not only aids in academic success but also in everyday decision-making and problem-solving.
Why are equivalent fractions important?
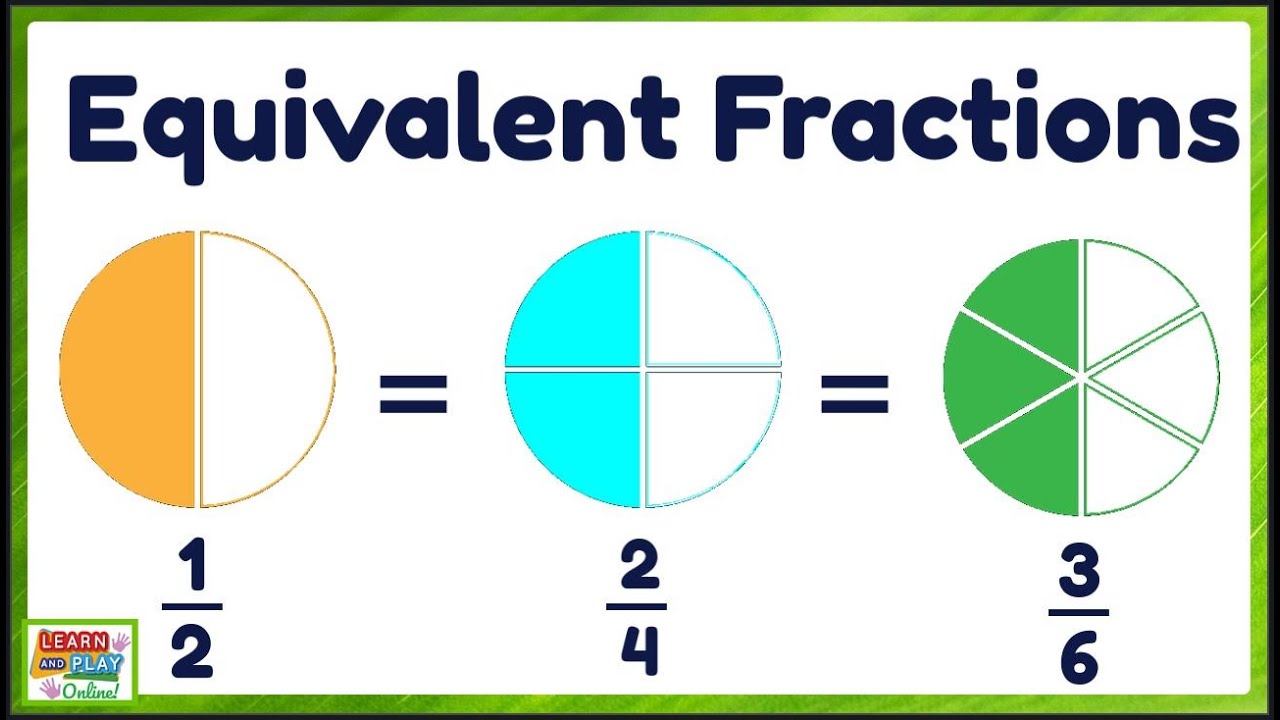
+
Equivalent fractions are essential for performing operations like addition, subtraction, and comparison of fractions. They help in simplifying calculations, understanding ratios, and dealing with proportions in real-life situations.
How do you know if two fractions are equivalent?

+
To check if two fractions are equivalent, multiply or divide both the numerator and the denominator of one fraction by the same number. If the resulting fraction is identical to the other fraction, they are equivalent. Alternatively, you can cross-multiply; if the cross-products are equal, the fractions are equivalent.
Can equivalent fractions be simplified?
+
Yes, equivalent fractions can often be simplified. Simplifying means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).