Simplify Math: Equivalent Expressions Worksheet Guide

A Beginner’s Guide to Simplifying Math with Equivalent Expressions

Mathematics can be daunting, but simplifying it through understanding equivalent expressions opens a door to making complex calculations much more manageable. Whether you're a student tackling algebra for the first time, or a math enthusiast seeking to solidify your foundational skills, this guide will walk you through the nuances of equivalent expressions in math. Let's dive into how you can work through these expressions with confidence.
What Are Equivalent Expressions?

Equivalent expressions in mathematics are different ways of writing the same value or function. They look different, but they represent the same mathematical idea when simplified or operated upon in the same context.
Examples of Equivalent Expressions

- Arithmetic: 5 * 2 and 10 are equivalent.
- Algebra: x + 1 and x - (-1) are equivalent.
- Fractions: \frac{3}{4} and 0.75 are equivalent.
Why Are Equivalent Expressions Important?

Understanding equivalent expressions helps in:
- Simplifying Calculations: By recognizing patterns or simplifying expressions, you can make problem-solving more efficient.
- Verifying Results: Expressing a solution in various forms can help verify its correctness through alternate methods.
- Enhancing Conceptual Understanding: Equivalent expressions allow for a deeper insight into how math works, beyond rote learning.
How to Identify Equivalent Expressions

Identifying equivalent expressions involves recognizing:
- Operations and Their Equivalents: Knowing how operations can be reordered or grouped in different ways (e.g., commutative and associative properties).
- Understanding Equality: Grasping that expressions that can be transformed into each other through algebraic manipulation are equivalent.
- Using Properties: Applying properties like the distributive property to expand or simplify expressions.
Steps to Identify Equivalence

- Expand or simplify each expression where possible.
- Apply algebraic properties to transform one expression into another.
- Check if both expressions yield the same result for a range of values.
Simplifying Expressions

Here's how you can simplify algebraic expressions to reveal their equivalence:
1. Combine Like Terms

This involves adding or subtracting terms with the same variables:
| Expression | Simplified Form |
|---|---|
| 5x + 3x | 8x |
| 9y^2 - 6y + 4 - y^2 | 8y^2 - 6y + 4 |

🔍 Note: Remember that like terms must have identical variable parts, e.g., all 'x' or 'y^2' terms.
2. Distributive Property

Use this property to distribute factors through expressions:
| Expression | Simplified Form |
|---|---|
| 2(3x + 5) | 6x + 10 |
| -1(7 - 2a) | -7 + 2a |
📌 Note: Distribution can be applied from left to right or right to left to achieve different but equivalent expressions.
3. Factoring Out Common Terms

The reverse of distributing, where you pull out common factors:
| Expression | Simplified Form |
|---|---|
| 2x + 4 | 2(x + 2) |
| 8x^2y + 4xy - 12y | 4y(2x^2 + x - 3) |
🔮 Note: Factoring out terms can reveal patterns or make an expression more manageable.
4. Reversing Operations

Operations can be reversed by applying their inverse:
| Expression | Simplified Form |
|---|---|
| (x + 3) - 3 | x |
| 2x/2 | x |
Using Equivalent Expressions in Problem Solving
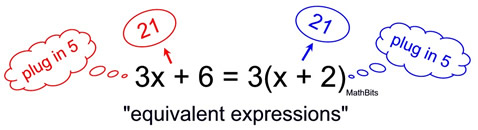
Here are some common scenarios where equivalent expressions are invaluable:
- Re-expressing Formulas: To solve for a different variable in an equation.
- Graphical Interpretations: Seeing different forms of an expression helps in graphing functions or understanding mathematical models.
- Comparisons: Comparing two expressions for equality can be simplified by converting them to equivalent forms.
In essence, equivalent expressions are not just about understanding algebra but also about seeing how math can be applied in various ways. They’re the building blocks for solving complex equations and interpreting data.
By now, you have learned about equivalent expressions, why they’re important, how to identify them, and simplify them for problem-solving. It’s a foundational skill that, once mastered, can lead to a greater appreciation and control over the language of numbers and variables.
Why do equivalent expressions matter in daily life?

+
Equivalent expressions help in everyday calculations, budgeting, understanding discounts, tax calculations, and even in programming, where different expressions can lead to the same outcome.
What if I can’t simplify an expression?

+
If an expression can’t be simplified further, it might already be in its simplest form, or there might be a restriction on the problem (like not using the distributive property). Check if there are any given constraints or if you’ve applied all applicable simplification rules.
Can equivalent expressions be used in trigonometry and calculus?

+
Absolutely. In calculus, equivalent expressions are crucial for techniques like integration by substitution or differentiation. In trigonometry, various identities are essentially equivalent expressions that make solving trigonometric equations much simpler.