Mastering Equations with Square Roots: Ultimate Guide

In the realm of mathematics, square roots stand as one of the most fascinating and essential concepts, providing us with tools to understand distances, solve quadratic equations, and much more. Understanding square roots is not just about solving puzzles; it's about applying a universal principle that applies across various mathematical disciplines. This ultimate guide will walk you through the intricacies of handling equations with square roots, offering insights, techniques, and practical applications.
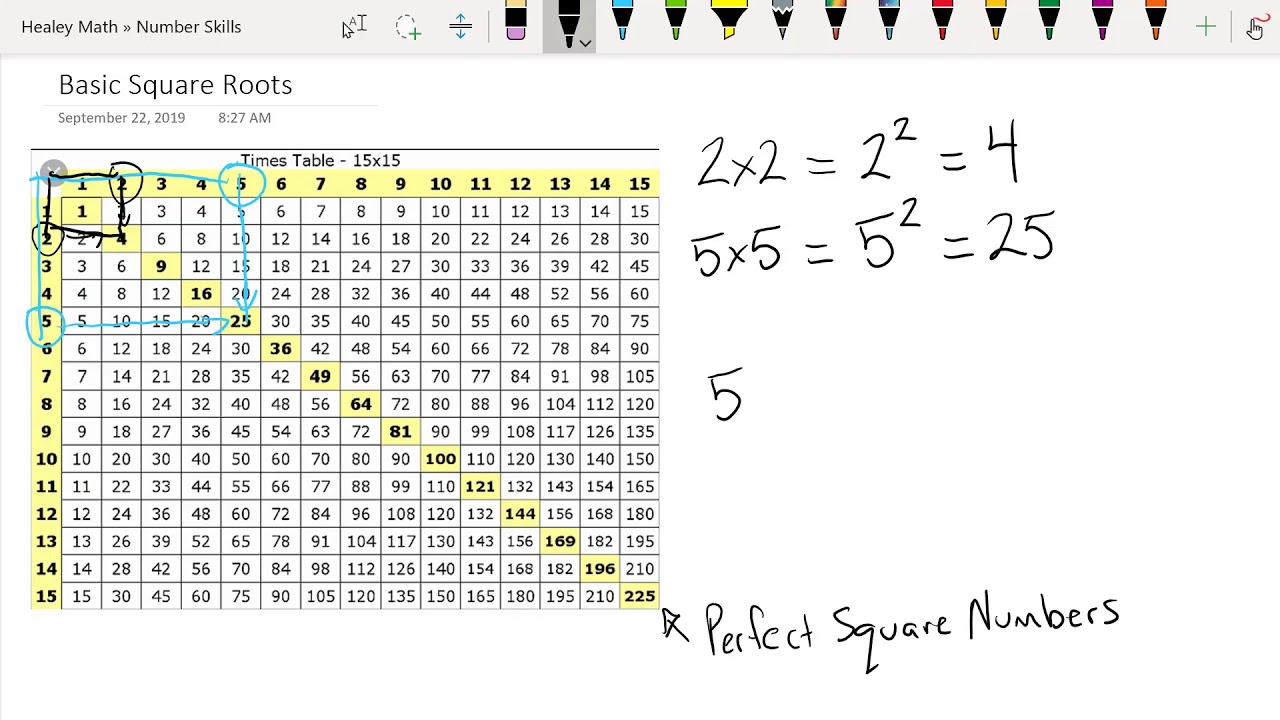
Understanding Square Roots

A square root of a number ( x ) is a number ( y ) such that ( y^2 = x ). Here are some key points:
- Principal Square Root: The positive value which when multiplied by itself gives the original number. For instance, the principal square root of 9 is 3.
- Negative Square Roots: Also exist, but in standard mathematics, we often focus on principal roots unless otherwise specified.
- Properties: Square roots exhibit special properties like if ( \sqrt{a} ) is known, then ( \sqrt{b} = \sqrt{ab} ), which is useful for simplifying equations.
Equations Involving Square Roots

Equations with square roots appear in various forms, and here are methods to solve them:
Isolating the Square Root
Often, equations include square roots alongside other terms. Here’s how to solve such equations:
- Move all terms without square roots to one side.
- Square both sides to eliminate the square root.
- Solve the resulting quadratic or linear equation.
⚠️ Note: Be cautious of extraneous solutions that might emerge when you square both sides.
Extracting Square Roots

When dealing with quadratic equations that can be expressed as perfect squares, one can often use:
- Move all terms to one side to form a perfect square trinomial.
- Extract the square root of both sides.
- Isolate the variable by solving for ( x ).
Practical Applications

Square roots aren’t just theoretical; they have practical applications:
- Distance Formulas: In coordinate geometry, the distance between two points ((x_1, y_1)) and ((x_2, y_2)) is calculated using square roots: [ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} ]
- Electrical Engineering: Root Mean Square (RMS) values in AC circuits involve square roots to calculate effective values of alternating currents.
- Physics: Kinematics often involves square roots to find velocities or distances, for example, using ( v = \sqrt{v_i^2 + 2a \Delta x} ).
Table: Key Square Roots

| Number | Square Root (Approximate) |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |

Advanced Techniques

The Babylonian Method

This iterative method for finding square roots is both efficient and straightforward:
- Estimate an initial guess.
- Compute ( n = (guess + \frac{x}{guess})/2 ).
- Iterate this process until desired precision is reached.
Challenges and Considerations

While solving equations with square roots, one must consider:
- Radical sign as a multivalued function, thus solving for both positive and negative roots.
- Checking for extraneous solutions since squaring can introduce non-solutions.
- The context of the problem, as some square roots yield complex or irrational numbers, which might not always have practical applications.
📘 Note: When dealing with radical equations, remember that the principal square root must be non-negative by definition, which sometimes requires additional algebraic manipulation or context to resolve correctly.
The intricacies of square roots span from simple arithmetic to complex problem-solving across mathematics and science. Mastering these skills enhances your ability to understand and work with many mathematical concepts, making square roots not just a calculation but a key to unlocking deeper mathematical principles. Whether you're solving equations, calculating distances, or working through practical applications, the universal principle of square roots remains a fundamental tool in your mathematical toolkit. As you continue your journey in mathematics, remember that every equation with a square root presents an opportunity to not only find an answer but to explore the beauty and elegance of numbers.
What is the difference between a square and a square root?

+
A square is the result when a number is multiplied by itself, while a square root is one of the two equal factors that multiply to give a number. The square of 5 is 25, whereas the square root of 25 can be either 5 or -5.
Can a square root be negative?

+
In standard arithmetic, we generally consider only the principal (positive) square root, but in a broader context, square roots do have both positive and negative values.
Why do extraneous solutions occur when solving square root equations?

+
Extraneous solutions arise because squaring both sides of an equation introduces the possibility of creating solutions that are not valid within the original equation, known as “adding false positives.”
How are square roots applied in real-world situations?

+
Square roots are applied in various fields such as calculating distances, determining the time it takes for objects to hit the ground (kinematics), AC circuit analysis, financial calculations (like the calculation of volatility), and more.
What are the limits of the Babylonian method for finding square roots?

+
While highly efficient for most numbers, the Babylonian method can become slow for very large numbers or extremely precise approximations, and it may not work well for numbers with no real square root.



