5 Steps to Master Domain and Range Worksheets
5 Steps to Master Domain and Range Worksheets

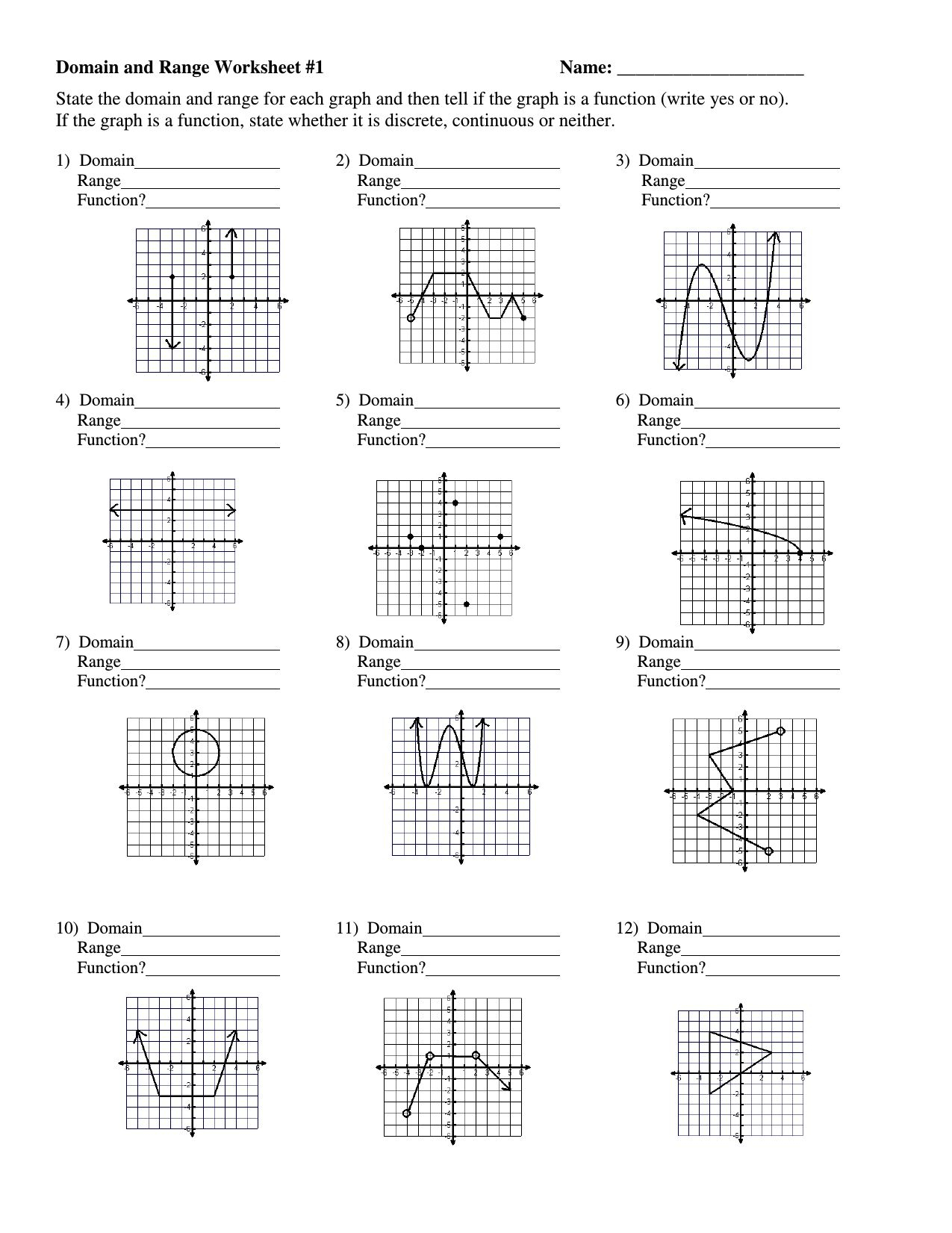
Domain and range worksheets are fundamental tools for understanding functions in mathematics. They help students grasp the concept of what values a function can take as inputs (domain) and what values can result from the function (range). Here's how you can master these worksheets effectively:
Step 1: Understand the Basics

Before diving into the worksheets, you must understand what domain and range mean:
- Domain: The set of all possible input values (or x-values) which can be plugged into a function.
- Range: The set of all possible output values (or y-values) which result from the function.
These concepts are crucial for analyzing graphs and equations. Here's how to approach them:
Identify the Functions

Work through examples where you identify:
- The type of function (linear, quadratic, rational, etc.)
- Any restrictions due to operations like division by zero or square roots
📝 Note: Functions like square roots only take positive inputs for real numbers, affecting their domain.
Step 2: Visual Analysis

Use graphs to visualize the behavior of functions:
Graphical Representation

When you look at a graph:
- The domain corresponds to all the x-values where the graph exists on the x-axis.
- The range includes all y-values covered by the graph.

Analyze Key Points

Identify:
- Vertical asymptotes (which indicate values excluded from the domain)
- Horizontal asymptotes (which can help determine the range)
- Holes in the graph (which indicate removable discontinuities)
Step 3: Algebraic Approach

Use algebraic methods to find domain and range:
Solving Equations

To find the domain:
- Solve for x in the equation, excluding any values that make the denominator zero or lead to square roots of negative numbers.
To find the range:
- Manipulate the function to find the set of y-values. This often involves solving for x in terms of y, but be cautious with quadratic functions where the range might be restricted.
📝 Note: For quadratic functions, the range can be limited by the vertex's y-coordinate, either an upper or lower bound.
Step 4: Use Domain and Range Worksheets

Practice with dedicated worksheets can reinforce these concepts:
Practice Makes Perfect

Here’s how to effectively use worksheets:
- Start with straightforward functions like linear and quadratic.
- Progress to more complex functions such as rational and trigonometric.
- Always check your work with provided solutions or examples.
When practicing:
- Explain to yourself why a value might be excluded from the domain or range.
- Sketch graphs to visualize your answers.
📝 Note: Referring to solutions after attempting problems can help in understanding common mistakes and approaches.
Step 5: Critical Thinking and Application

Once you feel confident:
Real-World Applications

Consider how domain and range apply in real-life scenarios:
- Modeling functions in economics, physics, or engineering.
- Interpreting data sets where domain and range play a role in describing trends or limitations.
Create Your Own Problems

Developing your own domain and range problems can:
- Strengthen your understanding by thinking like a creator.
- Help you anticipate and prepare for various types of functions.
📝 Note: Testing your own problems can reveal where your understanding still needs work or improvement.
In summary, mastering domain and range worksheets involves a multi-step process that begins with understanding basic principles, progresses through visual and algebraic analysis, and culminates in critical thinking and application. By following these steps, you can ensure a thorough grasp of these fundamental mathematical concepts, which are crucial for further studies in mathematics and science. Let's now address some frequently asked questions to provide additional insight into this topic.
How can I determine the domain and range from a graph?

+
The domain corresponds to the x-values where the function exists, and the range includes the y-values touched by the graph. Look for gaps or discontinuities that might indicate restrictions in domain or range.
What do asymptotes indicate about domain and range?

+
Vertical asymptotes indicate values excluded from the domain as they suggest division by zero. Horizontal asymptotes often show the range’s limits.
Why are domain and range important?

+
Domain and range provide insight into the behavior and limits of functions, which is essential for modeling real-world situations, analyzing data, and solving problems in various fields.